当前位置:网站首页>AcWing 1294.樱花 题解
AcWing 1294.樱花 题解
2022-07-06 09:14:00 【爱吃章鱼的怪兽】
AcWing 1294.樱花 题解
题目描述
给定一个整数 n n n ,求有多少正整数对 ( x , y ) (x,y) (x,y) 满足 1 x + 1 y = 1 n ! \dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{n!} x1+y1=n!1
输入格式:
一个整数 n n n
输出格式:
一个整数,表示满足条件的数对数量
答案对 1 0 9 + 7 10^9+7 109+7 取模
数据范围
1 ≤ n ≤ 1 0 6 1\le n \le 10^6 1≤n≤106
题解
观察式子,容易推出 x > n ! x > n! x>n! y > n ! y >n! y>n!
两个未知量 x , y x,y x,y, 知道其中一个后就能够推出另外一个
因此我们不妨设 y = n ! + k y=n!+k y=n!+k
变换后的式子为
1 x + 1 n ! + k = 1 n ! \dfrac{1}{x}+\dfrac{1}{n!+k}=\dfrac{1}{n!} x1+n!+k1=n!1
将式子两边通分可得 n ! ( n ! + k ) + ( n ! ) x = x ( n ! + k ) n!(n!+k)+(n!)x=x(n!+k) n!(n!+k)+(n!)x=x(n!+k)
变换可得
x = n ! ( n ! + k ) k = ( n ! ) 2 k + n ! x=\dfrac{n!(n!+k)}{k}=\dfrac{(n!)^2}{k}+n! x=kn!(n!+k)=k(n!)2+n!
由于x要满足正整数这一特性,所以问题转换成了k的值需要变成 ( n ! ) 2 (n!)^2 (n!)2的约数
问题变成了求一个数的约数
求约数可以用 算数基本定理
算术基本定理如下
任何一个正整数都可以用它的质因子唯一确定(其中 p i p_i pi为其质因子)
x = p 1 α 1 ⋅ p 2 α 2 ⋅ p 3 α 3 … ⋅ p n α n x=p_1^{\alpha_1} · p_2^{\alpha_2}·p_3^{\alpha_3}\dots·p_n^{\alpha_n} x=p1α1⋅p2α2⋅p3α3…⋅pnαn
根据全排列公式则其因子个数为
( α 1 + 1 ) ⋅ ( α 2 + 1 ) ⋅ ( α 2 + 1 ) ⋅ ( α 2 + 1 ) (\alpha_1+1)·(\alpha_2+1)·(\alpha_2+1)·(\alpha_2+1) (α1+1)⋅(α2+1)⋅(α2+1)⋅(α2+1)
问题变成了求解 ( n ! ) 2 (n!)^2 (n!)2的质因子和每个质因子的阶数
我们可以先求 ( n ! ) (n!) (n!)的质因子和每个质因子的阶数后将阶数乘2就可以的到 ( n ! ) 2 (n!)^2 (n!)2的解
如何求 ( n ! ) (n!) (n!)的质因子和质因子的阶数可以参考我的另一篇博客
求得 ( n ! ) (n!) (n!)的所有质因子后将质因子的阶数乘2,最后利用因子个数的计算公式就可以得到k的所有取值
对于每一个k值都有一个x值与其对应,则最后的所有取值即为正整数数对的个数
完整代码
import java.io.*;
import java.util.*;
public class Main {
static int n;
static final int N=1000010;
static final long MOD=1000000007;
static int[] Primes =new int[N];
static boolean[] isPrime =new boolean[N];
static int cnt=0;
static long ans=1;
public static void init(int n)//线性筛
{
Arrays.fill(isPrime,true);
for(int i=2;i<=n;i++) {
if (isPrime[i])
Primes[cnt++] = i;
for(int j=0;j<cnt;j++)
{
int p=Primes[j];
if(i*p>n)
break;
isPrime[i*p]=false;
if(i%p==0)
{
break;
}
}
}
}
public static void main(String[] agrs) throws IOException {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
n=Integer.parseInt(reader.readLine());
init(n);
for(int i=0;i<cnt;i++)//分解质因子
{
int tmp=n;
int p=Primes[i];
long res=0;
while(tmp>0)
{
res+=tmp/p;
tmp/=p;
}
res*=2;//转换成平方的质因子阶数
ans=(ans%MOD)*((res+1)%MOD);//因子计算公式
ans%=MOD;
}
System.out.println(ans);
}
}
边栏推荐
- Mysql21 - gestion des utilisateurs et des droits
- Ubuntu 20.04 安装 MySQL
- Some problems in the development of unity3d upgraded 2020 VR
- Have you mastered the correct posture of golden three silver four job hopping?
- CSDN问答标签技能树(二) —— 效果优化
- Navicat 导出表生成PDM文件
- MySQL主从复制、读写分离
- Asp access Shaoxing tourism graduation design website
- [ahoi2009]chess Chinese chess - combination number optimization shape pressure DP
- Data dictionary in C #
猜你喜欢
Did you forget to register or load this tag 报错解决方法
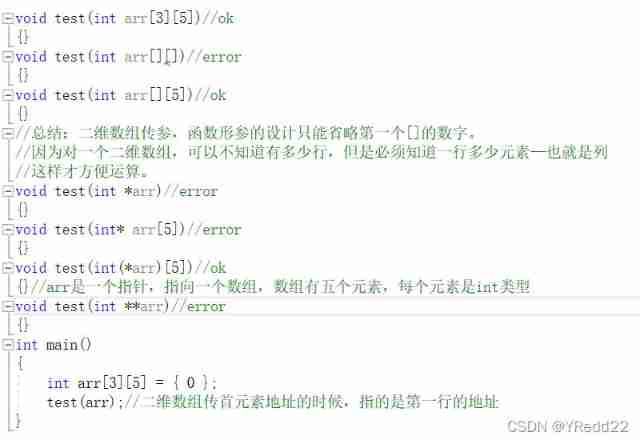
C language advanced pointer Full Version (array pointer, pointer array discrimination, function pointer)
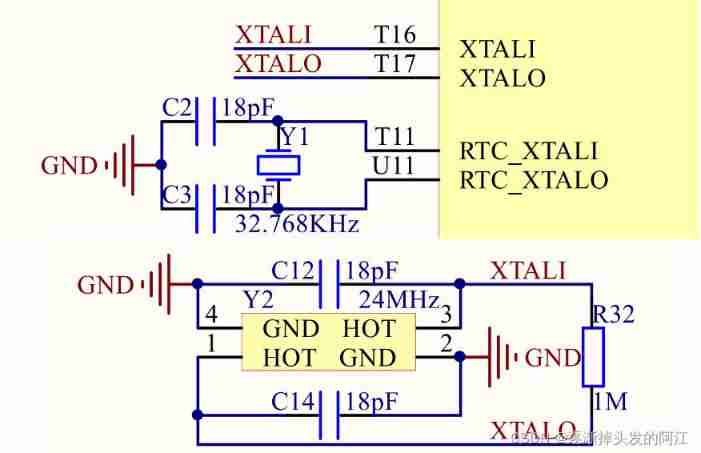
1. Mx6u learning notes (VII): bare metal development (4) -- master frequency and clock configuration
Why can't I use the @test annotation after introducing JUnit
Basic use of redis
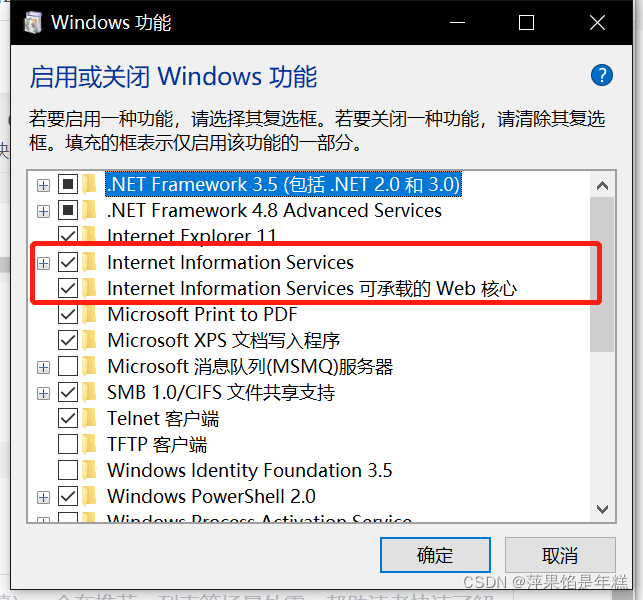
学习问题1:127.0.0.1拒绝了我们的访问

Solution: log4j:warn please initialize the log4j system properly
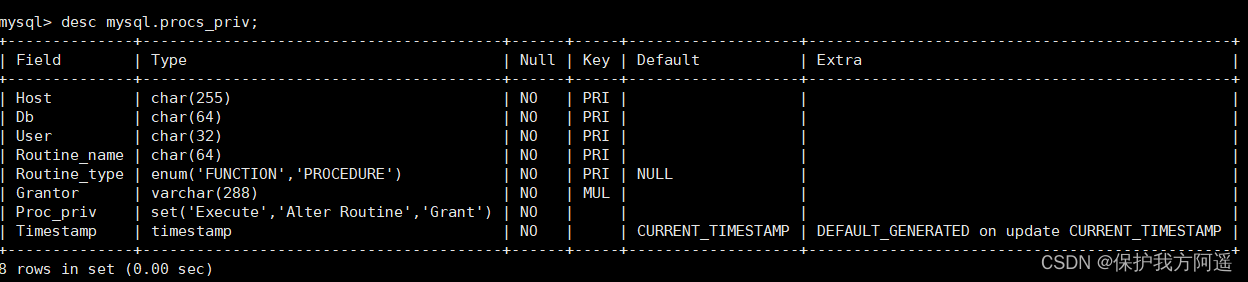
MySQL21-用戶與權限管理
![[recommended by bloggers] C WinForm regularly sends email (with source code)](/img/5d/57f8599a4f02c569c6c3f4bcb8b739.png)
[recommended by bloggers] C WinForm regularly sends email (with source code)

Breadth first search rotten orange
随机推荐
npm一个错误 npm ERR code ENOENT npm ERR syscall open
CSDN Q & a tag skill tree (V) -- cloud native skill tree
C语言标准的发展
PyCharm中无法调用numpy,报错ModuleNotFoundError: No module named ‘numpy‘
Kubernetes - problems and Solutions
Remember the interview algorithm of a company: find the number of times a number appears in an ordered array
@Controller, @service, @repository, @component differences
Invalid global search in idea/pychar, etc. (win10)
【博主推荐】C#生成好看的二维码(附源码)
Yum prompt another app is currently holding the yum lock; waiting for it to exit...
Postman Interface Association
QT creator create button
[recommended by bloggers] C # generate a good-looking QR code (with source code)
自动机器学习框架介绍与使用(flaml、h2o)
1. Mx6u learning notes (VII): bare metal development (4) -- master frequency and clock configuration
QT creator shape
Navicat 导出表生成PDM文件
QT creator design user interface
[Li Kou 387] the first unique character in the string
数数字游戏