Dynamic planning: robbing families and houses

Dynamic programming And raid homes and plunder houses

198. raid homes and plunder houses ●●

You are a professional thief , Plan to steal houses along the street . There is a certain amount of cash in every room , The only constraint on your theft is that the adjacent house is equipped with Interconnected anti-theft system , If two Adjacent houses were broken into by thieves on the same night , The system will automatically alarm .
Given an array of non negative integers representing the storage amount of each house , Count you Without triggering the alarm , The maximum amount that can be stolen overnight .
–
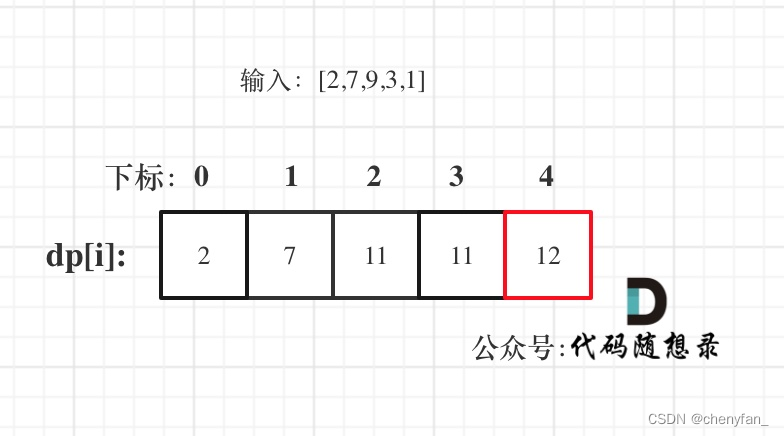
Input ：[2,7,9,3,1]
Output ：12
explain ： Steal 1 House No ( amount of money = 2), Steal 3 House No ( amount of money = 9), Then steal 5 House No ( amount of money = 1). Maximum amount stolen = 2 + 9 + 1 = 12 .

• Dynamic programming , Two dimensional array , Steal or not steal nums[i] Expressed as dp[i][1] and dp[i][0]

class Solution {
    
public:
    int rob(vector<int>& nums) {
    
        int n = nums.size();
        vector<vector<int>> dp(n, vector<int>(2, 0));
        dp[0][1] = nums[0];                 
        for(int i = 1; i < n; ++i){
    
            dp[i][0] = max(dp[i-1][0], dp[i-1][1]); //  Don't steal nums[i]
            dp[i][1] = dp[i-1][0] + nums[i];        //  steal nums[i]
        }
        return max(dp[n-1][0], dp[n-1][1]);
    }
};

• Dynamic programming , One dimensional array

1. dp[j]： Consider Subscripts j（ Include j） The houses within , The maximum amount that can be stolen is dp[j].
2. dp[j] = max(dp[j-1], dp[j-2] + nums[j]);
   Consider stealing or not stealing subscripts j
3. dp[0] = nums[0];
   dp[1] = max(nums[0], nums[1]);
4. Traversing from front to back

class Solution {
    
public:
    int rob(vector<int>& nums) {
    
        int n = nums.size();
        if (n == 0) return 0;
        if (n == 1) return nums[0];
        vector<int> dp(n, 0); 			// dp[j]
        dp[0] = nums[0];
        dp[1] = max(nums[0], nums[1]);	// 0  and  1  Only one can be stolen 
        for(int j = 2; j < n; ++j){
    		//  steal   or   Don't steal  nums[j]
            dp[j] = max(dp[j-1], dp[j-2] + nums[j]);
        }
        return dp[n-1];
    }
};

213. raid homes and plunder houses II ●●

You are a professional thief , Plan to steal houses along the street , There is a certain amount of cash in every room . All the houses in this place are Make a circle , It means The first house is next to the last house . meanwhile , Adjacent houses are equipped with interconnected anti-theft system , If two adjacent houses are broken into by thieves on the same night , The system will automatically alarm .
Given an array of non negative integers representing the storage amount of each house , Count you Without triggering the alarm device , The maximum amount you can steal tonight .

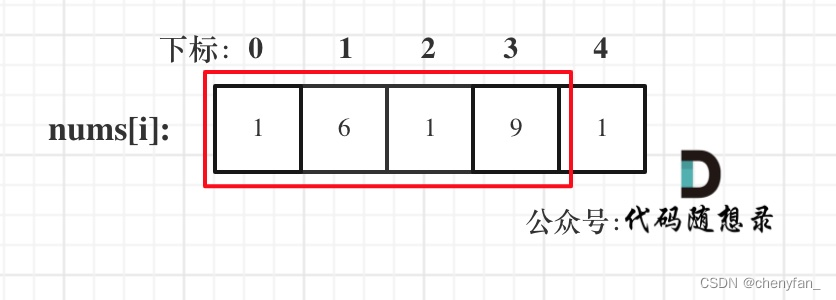
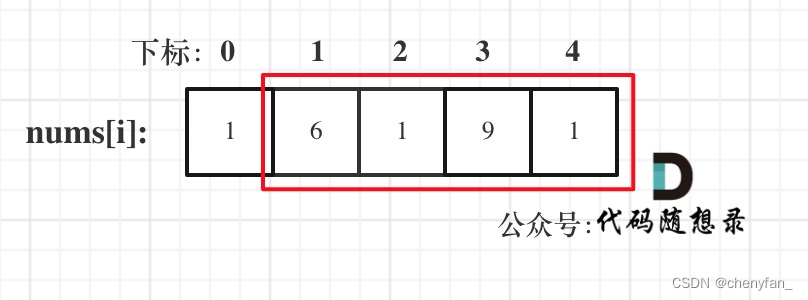
The house in this question End to end connection into a ring 了 , therefore , Divide the house into two situations , Turn into Two non looped The problem of house raiding is calculated separately ：

1. consider （ But not necessarily ） The first house , Not considering the last house ;
   
2. consider （ But not necessarily ） The last house , Not considering the first house .
   

class Solution {
    
public:
    int subRob(vector<int>& nums, int strat, int end){
    
        int n = end - strat + 1;        //  The number of subsets 
        if(n == 1) return nums[strat];
        vector<int> dp(n, 0); 
        dp[0] = nums[strat];
        dp[1] = max(nums[strat], nums[strat + 1]); 
        for(int j = 2; j < n; ++j){
    
            dp[j] = max(dp[j-1], dp[j-2] + nums[j+strat]);
        }
        return dp[n-1];
    }
    
    int rob(vector<int>& nums) {
    
        int n = nums.size();
        if(n == 1) return nums[0];
        int strat = subRob(nums, 0, n-2);   // [0, n-2]
        int end = subRob(nums, 1, n-1);     // [1, n-1]
        return max(strat, end);
    }
};

337. raid homes and plunder houses III ●●

The thief found a new area to steal . There is only one entrance to the area , We call it root .
except root outside , Each house has and only has one “ Father “ The house is connected to it . After some reconnaissance , The clever thief realized that “ All the houses in this place are arranged like a binary tree ”. If Two directly connected houses were robbed the same night , The house will alarm automatically .
Given a binary tree root . return Without triggering the alarm , The maximum amount a thief can steal .

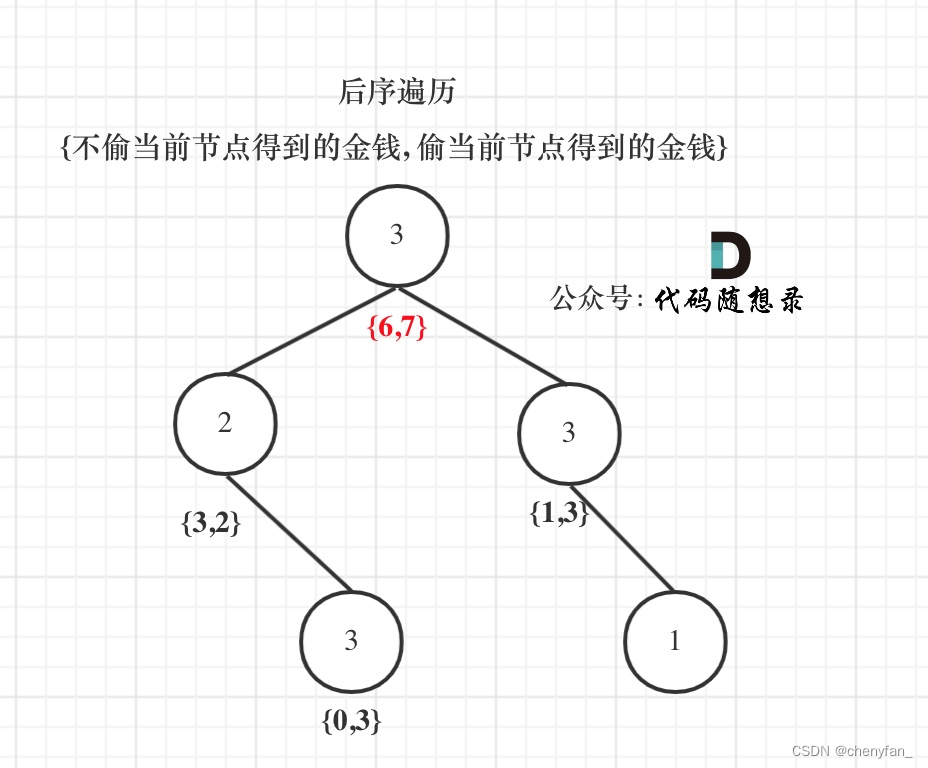
After the sequence traversal , Through the return value of the recursive function to do the next calculation .

If steal The current node , Two children can't move , and Recursion to grandchildren ;
If Don't steal Current node , You can consider stealing around children （ Notice what's going on here “ consider ”）

1. Memory recursive search

Avoid double calculation of nodes , Use the hash table to store the calculated node amount .

• Time complexity ：$O(n)$
• Spatial complexity ：$O(\log n)$, Count the space of the recursive system stack

class Solution {
    
public:
    unordered_map<TreeNode*, int> map;
    int rob(TreeNode* root) {
    
        if(root == nullptr) return 0;
        if(root->left == nullptr && root->right == nullptr) return root->val;   //  Leaf node , Direct return value 
        if(map[root]) return map[root];     //  Mnemonic search hash 
        //  Steal the parent node , Recursively traverse grandchildren 
        int val1 = root->val;
        if(root->left != nullptr) val1 += rob(root->left->left) + rob(root->left->right);
        if(root->right != nullptr) val1 += rob(root->right->left) + rob(root->right->right);
        //  Don't steal the parent node , Recursive traversal of child nodes 
        int val2 = rob(root->left) + rob(root->right);
        //  Taking the maximum , And store memory 
        map[root] = max(val1, val2);
        return map[root];
    }
};

2. Dynamic programming （ Tree form dp）

The above memory search is for a node Steal and don't steal The biggest money you get is not recorded , It requires real-time calculation and comparison .

Dynamic programming is actually using state transition container array dp[] To record changes in state ,
dp[0] Indicates the maximum amount obtained by not stealing this node ,
dp[1] Indicates the maximum amount obtained by stealing this node .

• Time complexity ：$O(n)$, Each node is traversed only once
• Spatial complexity ：$O(\log n)$, Count the space of the recursive system stack

class Solution {
    
public:
    vector<int> robTree(TreeNode* root) {
      
        if(root == nullptr) return {
    0, 0};
		vector<int> dp(2, 0);
		
        //  Consider the child node 
        vector<int> left = robTree(root->left);
        vector<int> right = robTree(root->right);

        //  Do not steal this node , Subscript to be 0, Child nodes can be stolen, not stolen 
        dp[0] = max(left[0], left[1]) + max(right[0], right[1]);
        //  Steal this node , Subscript to be 1, You can't steal children's nodes 
        dp[1] = root->val + left[0] + right[0];
    
        return dp;
    }

    int rob(TreeNode* root) {
    
        vector<int> ans = robTree(root);
        return max(ans[0], ans[1]);
    }
};