当前位置:网站首页>【经典控制理论】自控实验总结
【经典控制理论】自控实验总结
2022-07-05 23:03:00 【robinbird_】
※自控系统脚本编写
1、变量
sym, syms 符号变量
sym a; syms a b; f = str2sym('a+ b^2');
2、基本操作
求导
dfa = diff(f函数,a对哪个变量求(偏)导);积昏
intb = int(f函数,b对哪个变量求积分,b1,b2区间);拉氏变换
%t还是得事先定义好,s求拉氏变换时会自带 ft = exp(2*t); L1 = laplace(ft);拉氏反变换
ftt = ilaplace(L1);
3、控制系统模型
多项式形式(传递函数模型)
系数连续存于一个数组中,分子分母各一个数组,从高次到低次传
num = [1 2 3]; %分子对应的系数 den = [4 5 6 7]; %分母对应的系数 gs = tf(num,den);
零极点模型
需要两个数组,同上,加一个k增益
z = [1 2 3]'; %零点,注意加转置 p = [4 5 6 7]; %极点 k = 9; gs2 = zpk(z,p,k);
互相转换
[num,den] = zp2tf(z,p,k); %零极点转传递函数其他表达
分子/分母表达式有zpk类型,但是需要tf格式时,使用conv(就是多项式乘法)统一转化为多项式类型,例如
num = [1 2.9 2]; den = conv([1 0],[1 10 25]); gs = tf(num,den); %后面要画根轨迹图
4、模型的连接
串联— series
[num3,den3] = series(num,den,num2,den2);并联— parallel
[num3,den3] = parallel(num,den,num2,den2);反馈— feedback
[num3,den3] = feedback(numg,deng,numh,denh,sign); %先给G(s)的传递特征,再给H(s)的传递特征,最后sign是默认-1(负反馈),可以改+1(正反馈)单位反馈— cloop
[num3,den3] = cloop(numg,deng,sign); %和上面比少传H(s)
5、典型输入函数
单位阶跃函数— step
t = [0:0.1:100]; num = 1; den = [1 0.4 1]; step(num, den, t); %t主要是得说明要画多长t的ct图像,num,den直接传闭环传递函数的特征数组了单位脉冲函数— impulse
t = [0:0.1:100]; num = 1; den = [1 0.4 1]; impulse(num, den, t); %t主要是得说明要画多长t的ct图像,num,den直接传闭环传递函数的特征数组了自定义输入— lsim
t = 0:0.1:10; %u用含t的表达式即可,比如 u = t; %或者 lsim(num,den,u,t); lsim(z,p,k,u,t); %仍然是开始给出系统闭环传递函数的特征,如上两种形式均可,u是输入的r(t),用含t的表达式整,t是时间 %例如,这个用于频率特性测试时,给系统输入一个正弦函数 t = [0:0.001:10]; rt = 1* sin(15 * t); lsim(nums,dens,rt,t);注意:以上所有的函数使用后,如果用其返回值,则默认直接单窗口绘图;而如果使用一个变量存返回值(就是系统输出的结果,是一个一维数组),之后可以用于多图的绘制
6、3种系统特性图像
根轨迹绘制
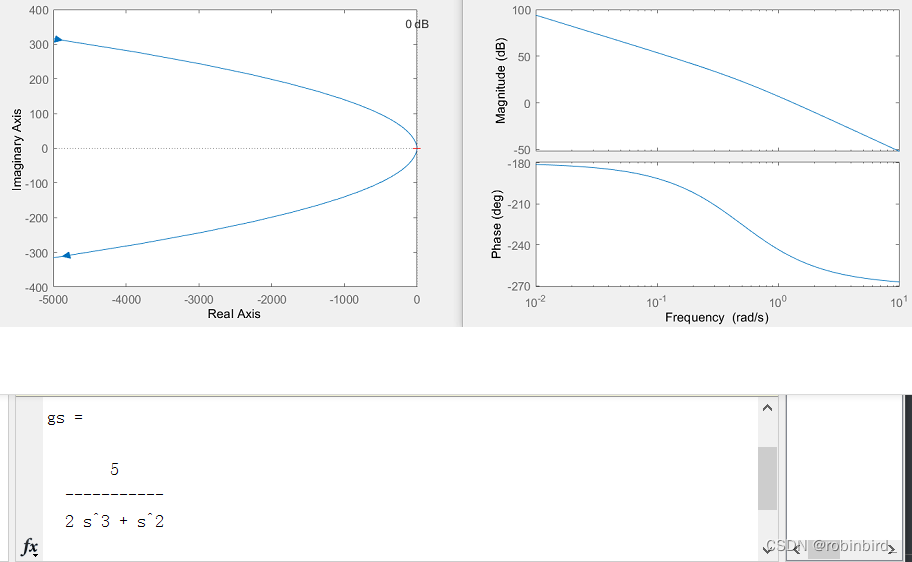
gs = tf(num,den); rlocus(gs); %给的是完整的函数表达,且这里开环传函的首一表达式(不含根轨迹增益K*)奈奎斯特图
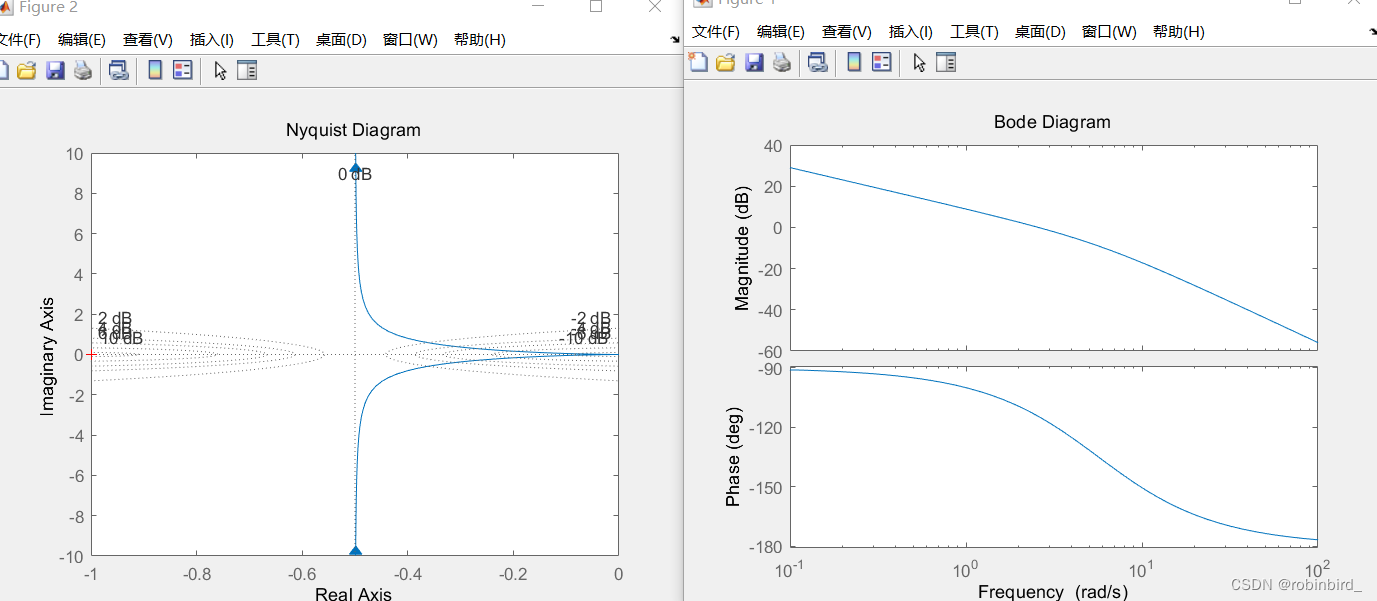
matlab画出来包含了w从0到-∞的轨迹,与正的部分完全对称,不用管
nyquist(gs); %传参传 开环传函表达式bode图
bode(gs); %同前,一般画的是开环的对数幅频图,那就给开环的表达式例如,左根轨迹,右bode图
7、matlab绘图大法
基本绘图设置
grid; %添加网格 xlabel("标题名"); %设置横坐标轴名称 ylabel("同上"); %纵坐标轴名称 title("abb"); %绘制的图像名称多图绘制
(1)一个窗口画一张图,注意,grid和legend这类特殊要求不是作用于所有窗口的,每个figure有需要都要单独添加
figure; %code,绘制一张图 figure; %code,绘制另一张图,以此类推 %举例,先画了一个bode图,再画了一个奈奎斯特图 figure; z = [-0.2]; p = [0 -0.1 -4]; k = 16; [num,den] = zp2tf([],[0 -4*sqrt(2)],k); tf_gs = tf(num,den); bode(tf_gs); figure; nyquist(tf_gs); grid; %attention
(2)多图绘制于一个窗口
首先需要不让matlab将响应直接绘制,就用变量接收返回值
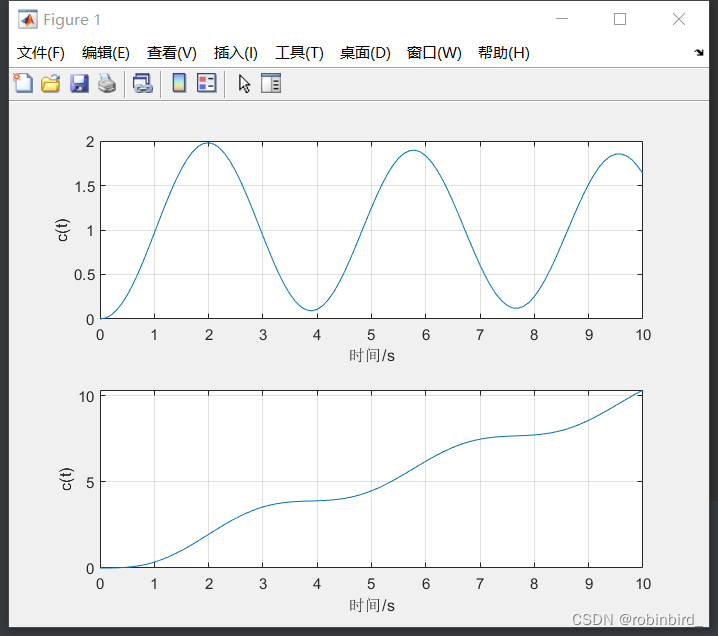
t = 0:0.1:10; y_step = step(numfi,denfi,t); %接收返回值 u = t; y_ramp = lsim(numfi,denfi,u,t); %接收返回值 接着使用类似于前面的格式,subplot的参数参考这篇文章:http://t.csdn.cn/pXIZ5
subplot(x1,y1,z1); plot(t1,c1); axis normal; subplot(x2,y2,z2); plot(t2,c2); axis normal; %举例,接前面的内容 subplot(2,1,1); plot(t,y_step); xlabel("时间/s"); ylabel("c(t)"); grid; axis normal subplot(2,1,2); plot(t,y_ramp); xlabel("时间/s"); ylabel("c(t)"); axis normal grid;
※simulink插件仿真
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WYEGSDxt-1657012369295)(C:\Users\robinbird\AppData\Roaming\Typora\typora-user-images\image-20220421104137653.png)]](/img/e5/8b609ccabbd25ebe5fbada29686760.png)
常用元器件库名称
下面的就是,在元器件库直接对相应的名字搜索就可以得到
增益K gain
传递函数
多项式类型 transfer fcn:
零极点模型 Zero-Pole
示波器 scope
斜坡信号 ramp
阶跃信号step
正弦信号 sine wave
求和 sum
死区模块 dead zone
限幅模块 saturation
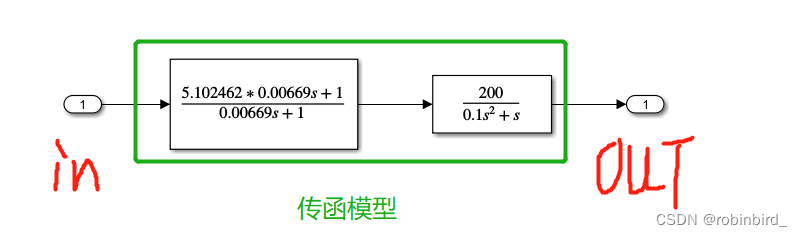
传递函数的系统特性图分析
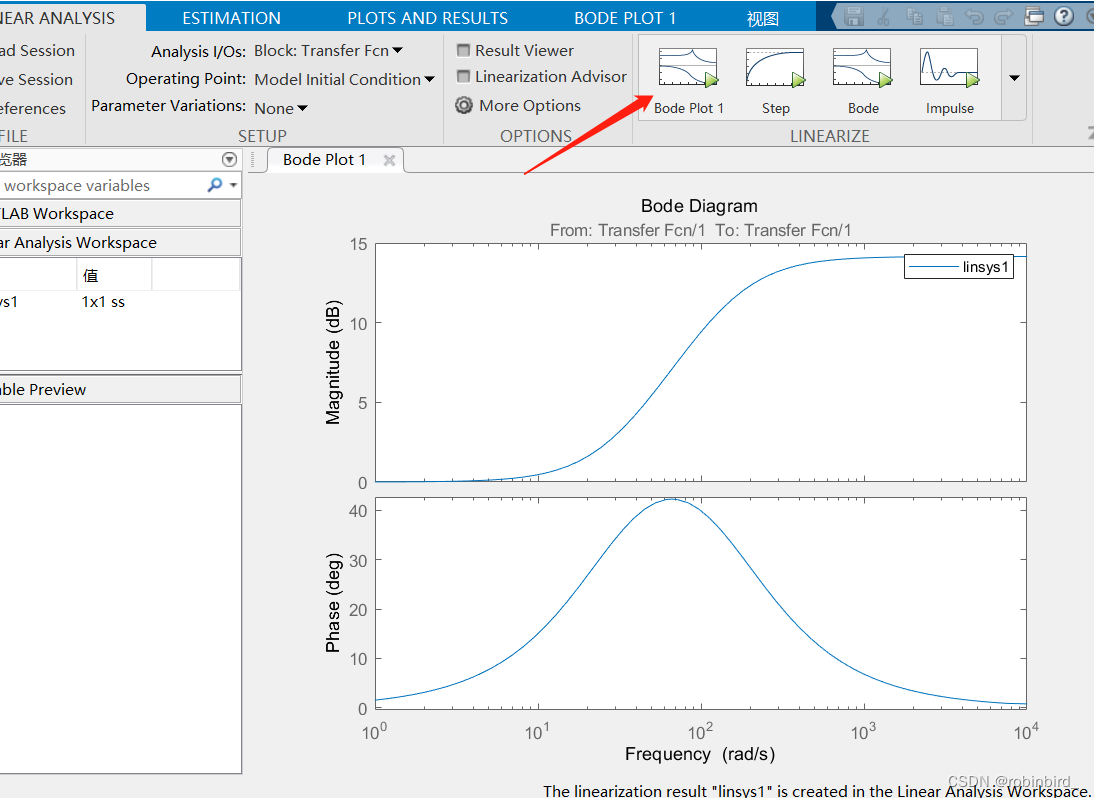
先利用in和out模块,搭建如下模型
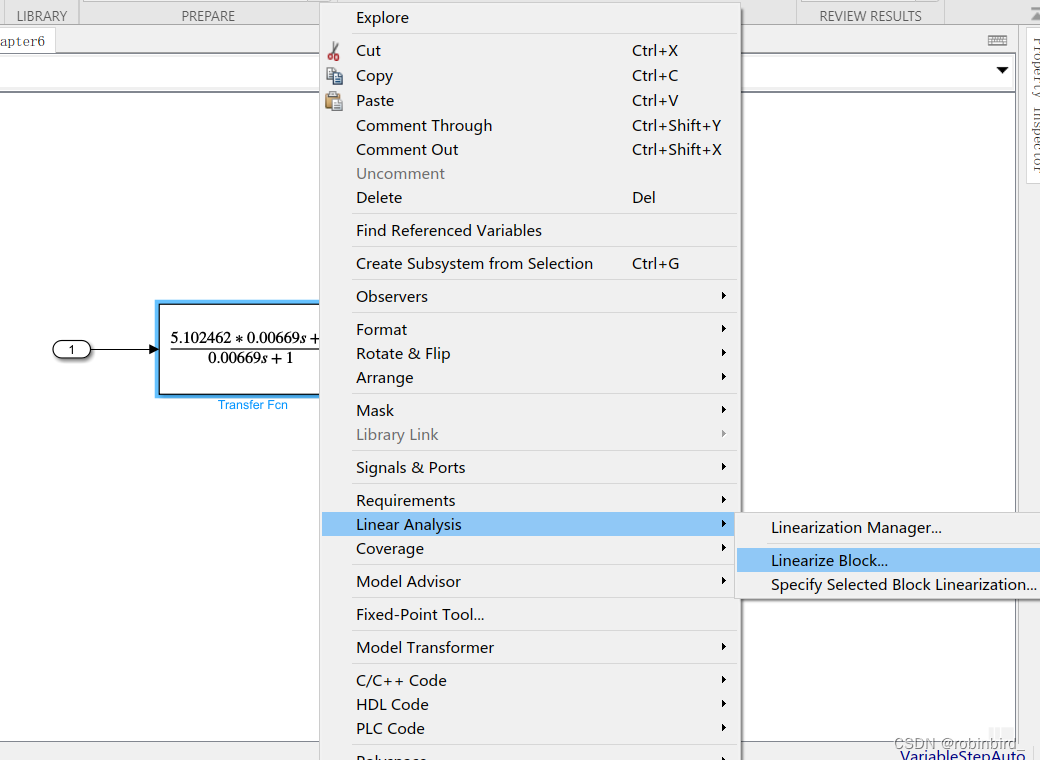
对一个传函模块,右键,找到Linearize block
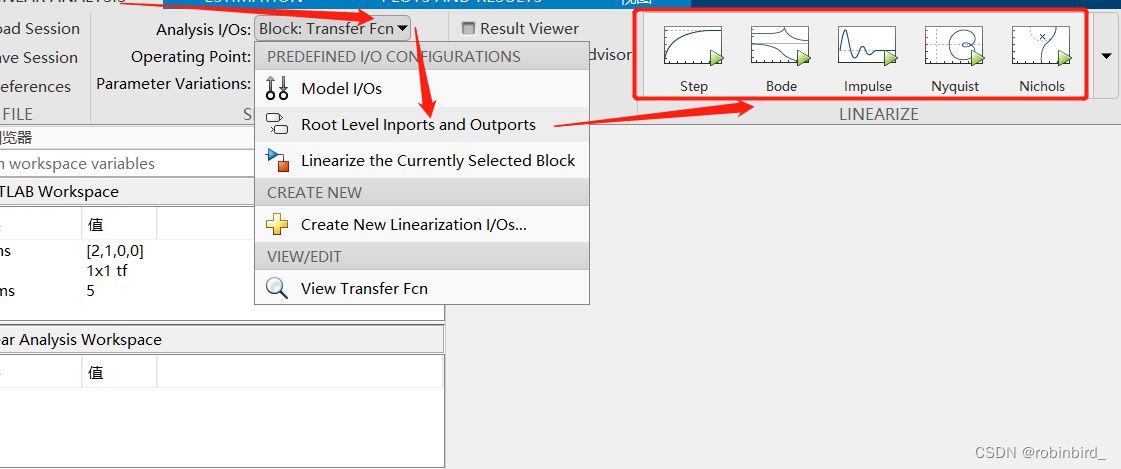
将输入输出的来源选择为如下图所示,之后点击想获取的系统特性曲线,就可以直接绘制了
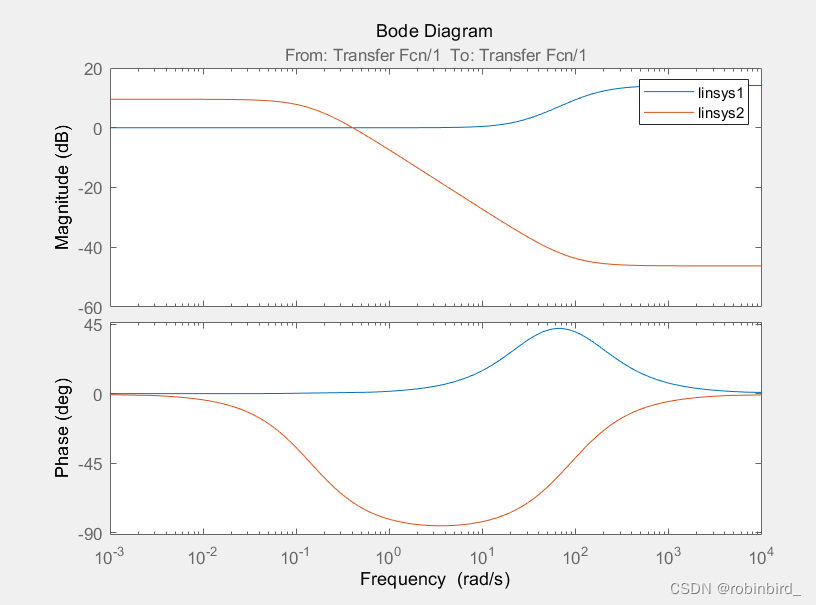
如果想在同一张图上绘制多条曲线(多用于系统校正),就在第一次画出图后,(自己对simulink的模型简单修改参数值后),再点击当前plot的按钮,就有两张图了,按照此方式叠加
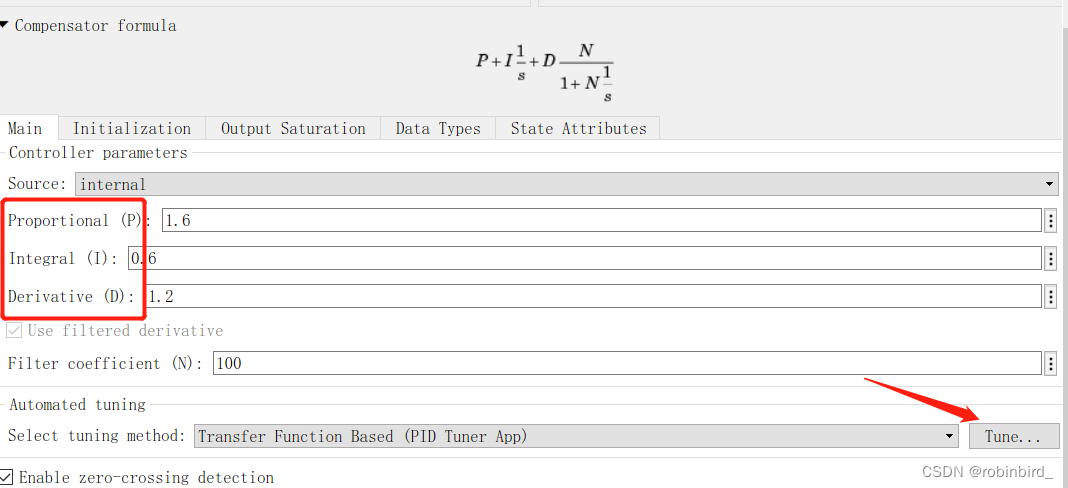
PID模块 PID controller
对应修改PID三个参数即可
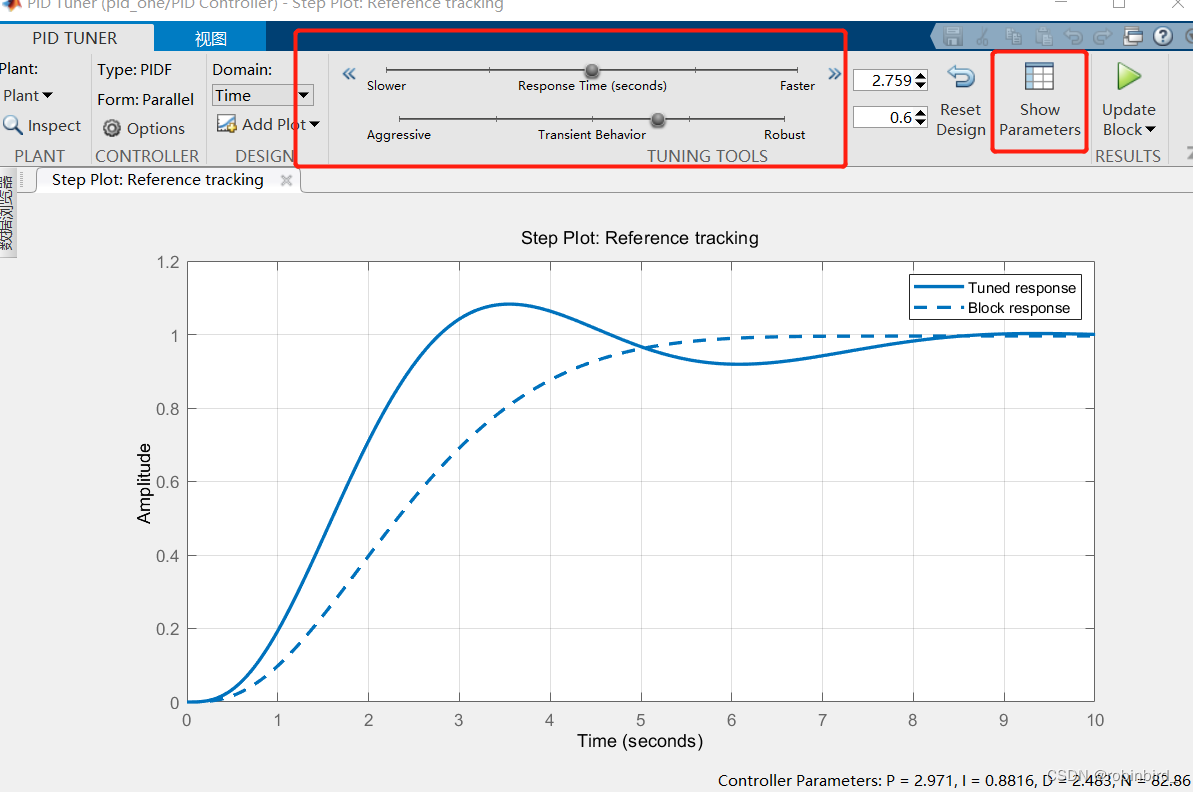
还可以使用PID tunner即时调节快速性和波动性,见下图
※脚本和simulink梦幻联动
将simulink仿真数据用.m脚本处理
直接用传递函数模型,再通过一个simout把数据传出来就是
几种设置模式
structure with time
这个有时间和对应的输出
plot(out.so.time, out.so.signals.values); %out应该是必加so给simout命的名字,这个可以自定义,因为一个.slx可以有很多歌simout模块
structure
只有输出
yt = out.so.signals.values;array
只有输出,以数组形式返回
plot(out.so);timeseries
plot(out.so.Time,out.so.Data);用.m绘制李萨如图形/时域响应曲线
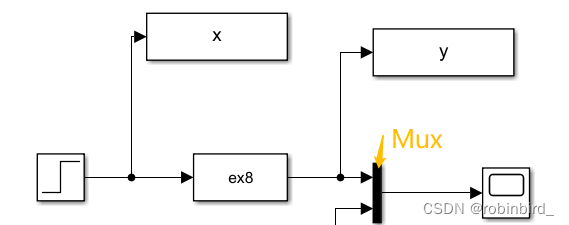
这里直接用自控第八次实验的代码了
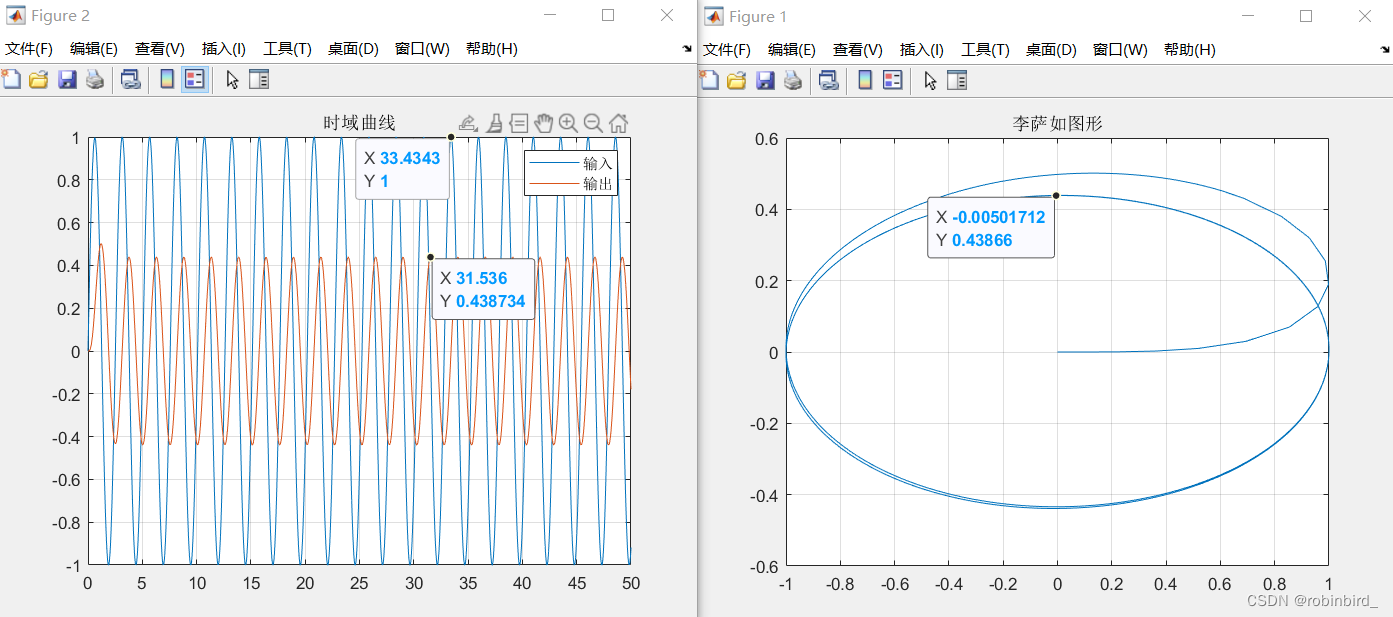
figure; plot(x.signals.values,y.signals.values); title("李萨如图形"); grid; figure; plot(x.time,x.signals.values); hold on; plot(y.time,y.signals.values); legend("输入","输出"); title("时域曲线"); grid;可以用x(对应着系统的输入),和y(对应系统的输出)直接用matlab拟合
注意:先将x,y的数据类型设置为2-D array,就是二维数组,再按照下面文章的步骤进行数据导入:
http://t.csdn.cn/NrfDU
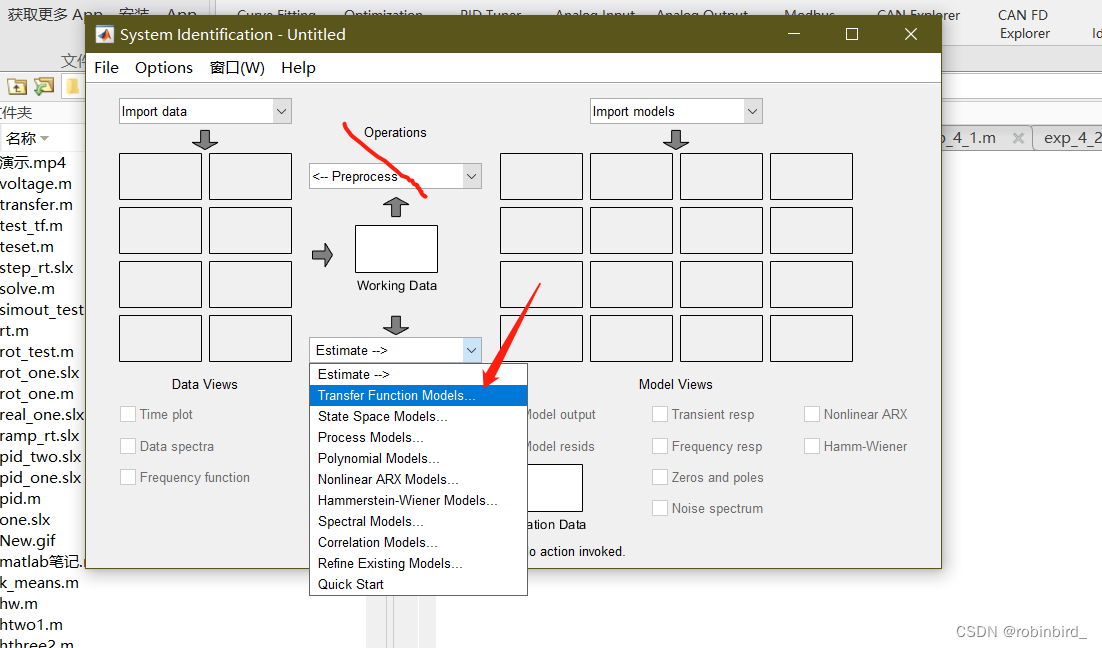
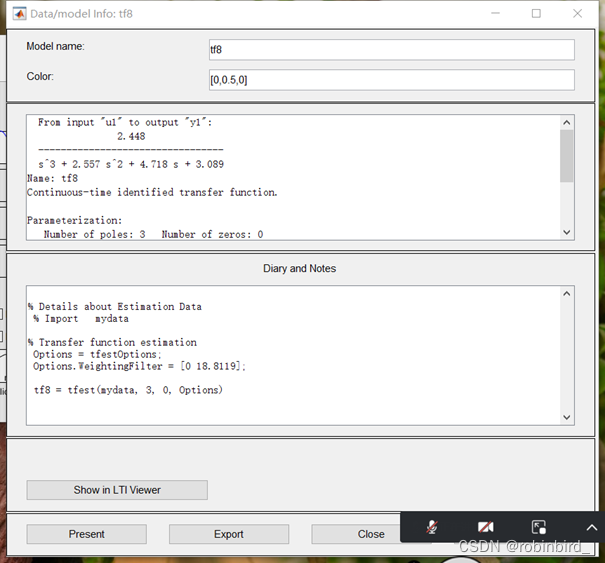
接下来分析环节:operations个人觉得不需要,分析方式就用传函模式,需要给出它的零极点个数,matlab根据零极点数量直接拟合
以自己第八次实验的截图为例,当时选择的无零点,3个极点
※自控原理补漏~~(某菜狗考完试才弄明白)~~
主要是与高阶系统利用主导极点降阶法和频率测试有关,结合自控的具体实验内容简单阐述一下
1、高阶系统主导极点降阶
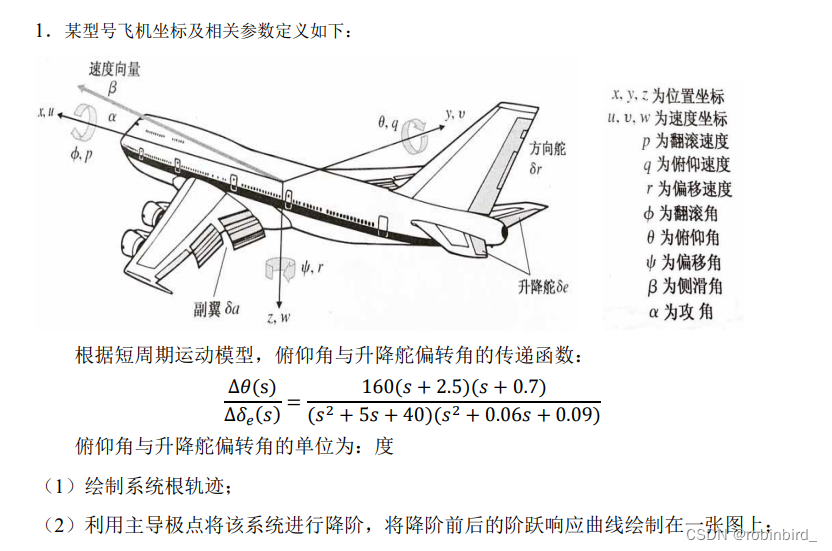
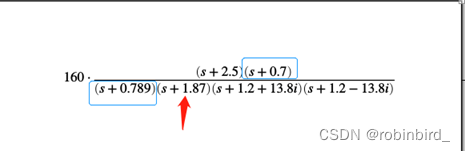
题目(第一问忽略):
个人理解:给出的传函就是这个系统的开环传递函数,且对应根轨迹增益为160,要绘制那就得到不含160的传函作为参数传给rlocus绘图即可;
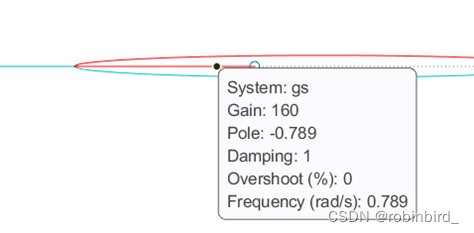
而对于降阶,则需要得到在K*=160的所有根,其实用matlab绘制的根轨迹图去图中找4个根不如直接上卡西欧991解方程香,直接得到更精确的结果,教程见
fx-991CN X方程(组)求解功能的使用 - 電卓院亜紀良的文章 - 知乎 https://zhuanlan.zhihu.com/p/28795401
理论知识补充:先膜一波哈工大巨佬的讲解:https://www.bilibili.com/video/BV1cK4y1U7jR?share_source=copy_web
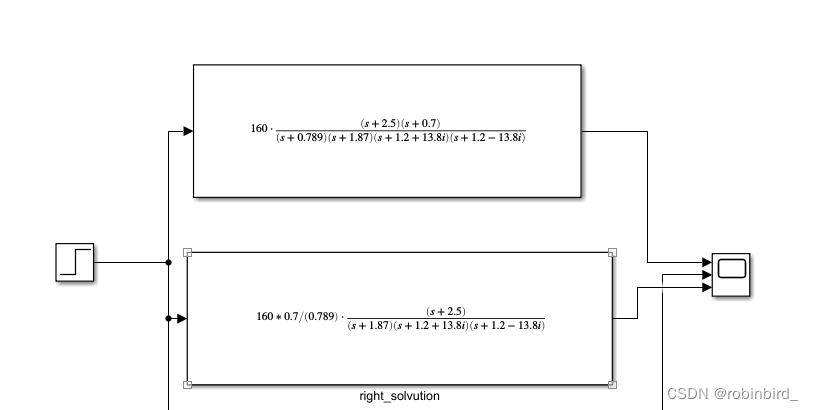
对于高阶系统的降阶,需要保证降阶前后系统的闭环增益不变,所以最好的方式还是得到系统的闭环传函,写为闭环零极点形式,接着分析闭环零极点的位置,有一对十分接近的零极点(偶极子,蓝色框中的),可以去除,剩余的极点的实部并没有2-3倍以上的关系,所以均不能省去
结果:按照K不变的原则,去掉谁就把对应的常数项留下,最后获得阶跃响应曲线
2、频率特性测试
题目:
补充:
(1)关于相位和幅度的求解如下,所以只需要在李萨如图像(x为输入,y为输出)中寻找到图像与x=0轴的交点,在阶跃响应曲线中找到输入输出图像的峰值整理成表格,画图即可
R ( t ) = A 0 ∗ s i n ( w t ) C ( t ) = A 1 ∗ s i n ( w t + φ ) A ( w ) = A 1 / A 0 φ ( w ) = a c r s i n ( C ( 0 ) / A 1 ) R(t) = A_{0}*sin(wt)\\ C(t) = A_{1}*sin(wt+φ)\\ A(w) = A1/A0\\ φ(w) = acrsin(C(0)/A1) R(t)=A0∗sin(wt)C(t)=A1∗sin(wt+φ)A(w)=A1/A0φ(w)=acrsin(C(0)/A1)
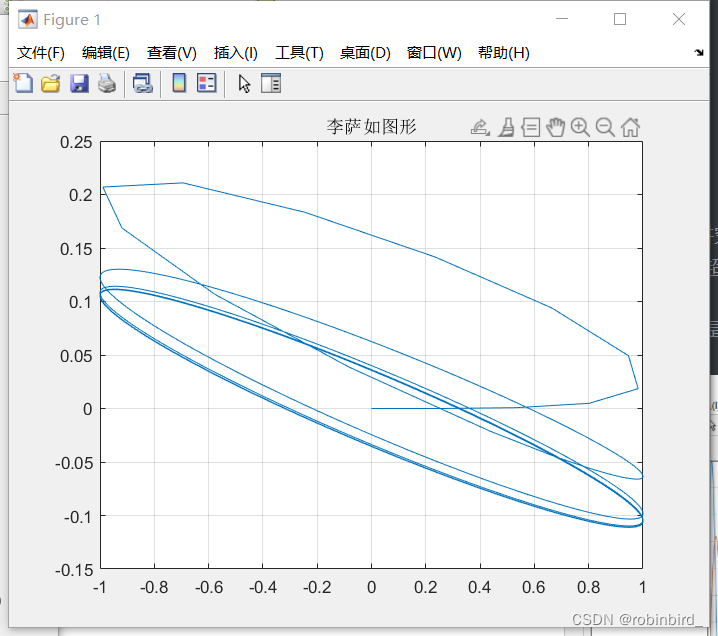
(2)相位也有讲究,李萨如图像是椭圆的,其长轴倾斜的角度(与正x轴夹角)也就大概是相位差,所以要注意相位超越90°/180°/270°等,及时修改对应的相位求解公式比如这个图,就是正椭圆,相位接近90°
这个就是已经超过90°了
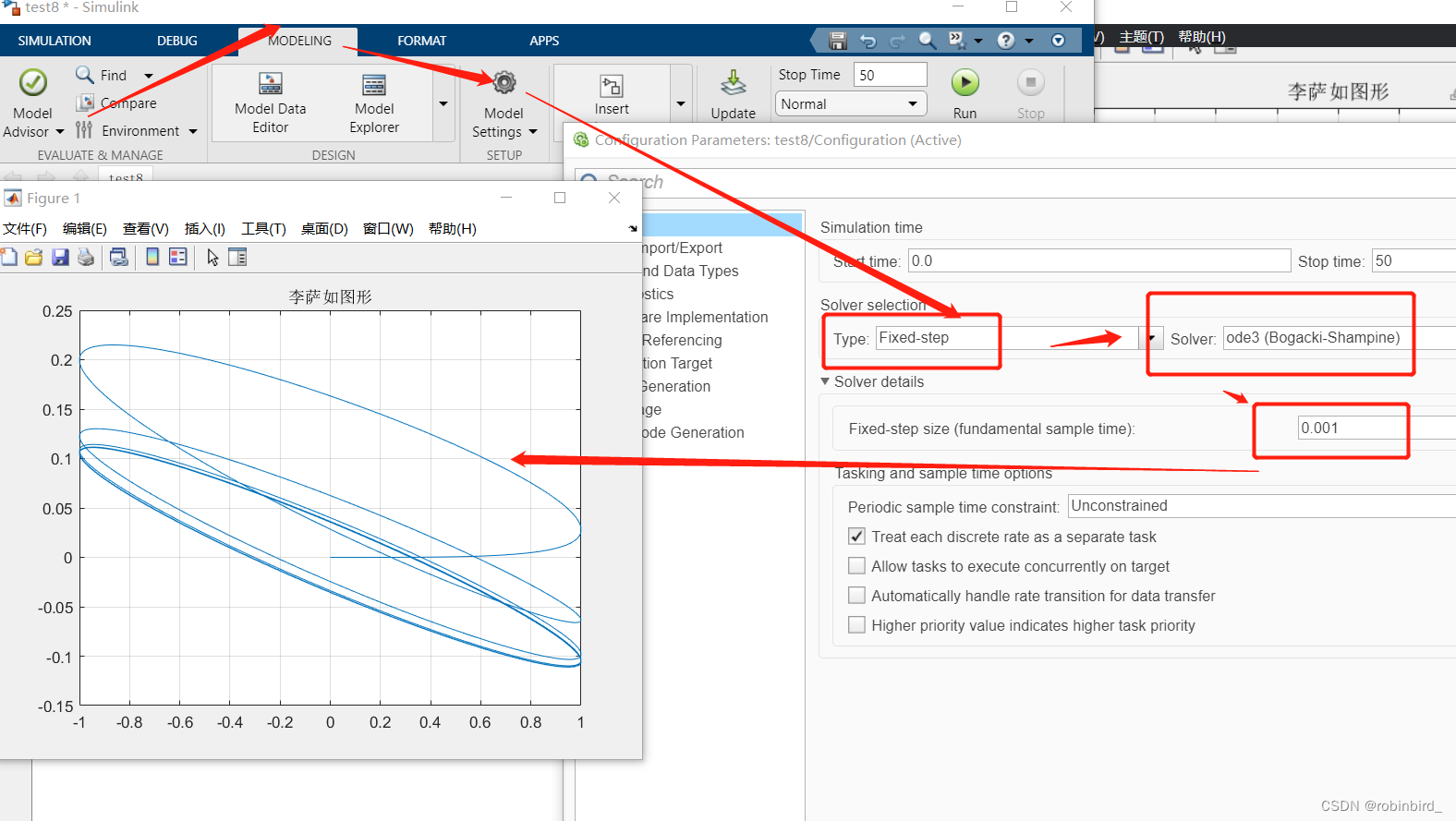
(3)但是你可以发现上面的曲线并不够光滑,于是我抄了之前老师发过的类似的模型设置,曲线瞬间美丽:在simulink界面里面寻找这个设置
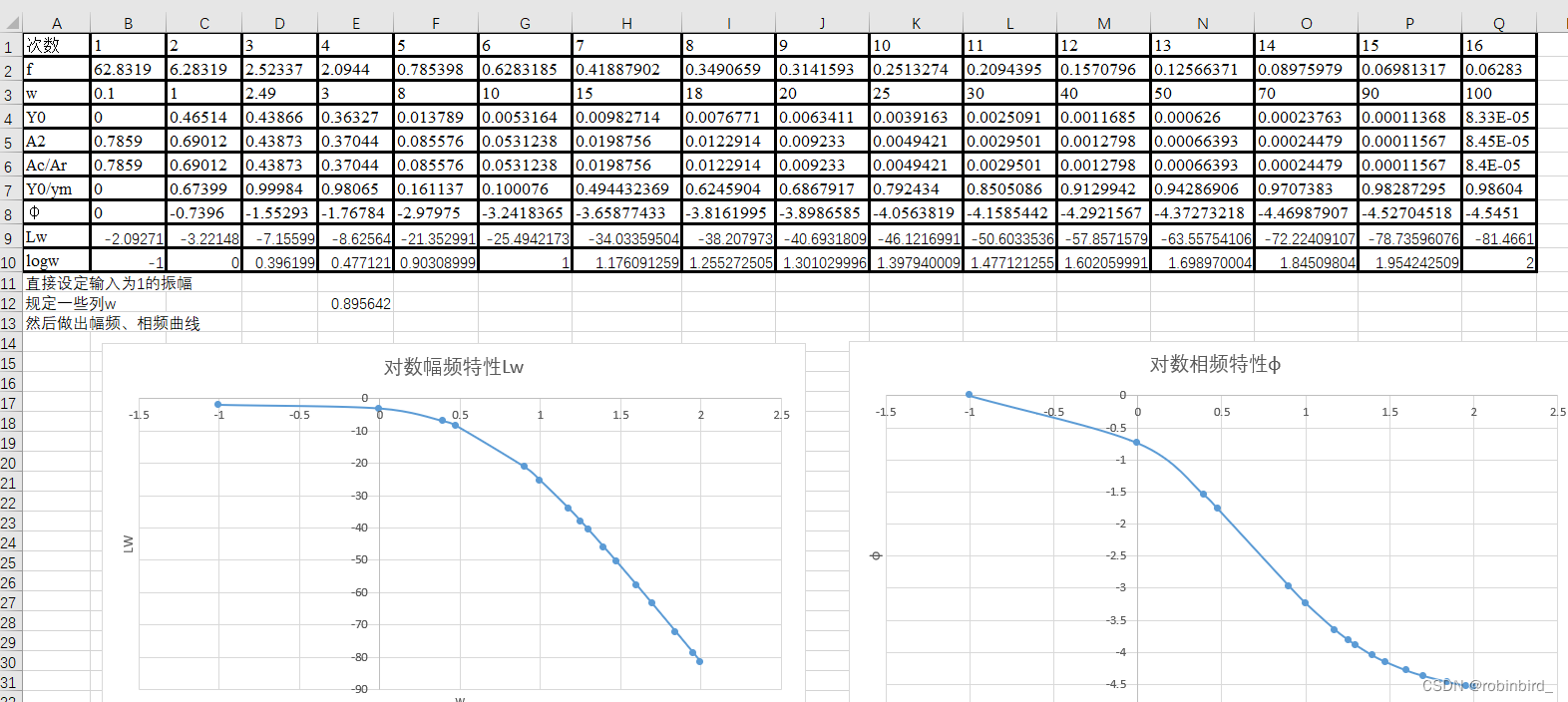
(4)接下来是excel处理部分,整理好w/A1/A0/C0并使用excel的函数,利用散点图带渐近线的类型,就可以得到频率特性测试的图像,并根据最大相位、转折点、初相位、初幅度等进行判断
(5)虽然显然是3阶系统,但是用二阶系统的分析方式居然也还行、、、但是不建议这样搞,
system identification它不香吗;其他的方式,比如通过阶跃响应的曲线也可以得到一些信息从而拟合该函数也是考完试才解决的疑惑(纯纯是因为自己撒币了):bode图针对的就只是传递函数的表达式,与开环闭环没有啥关系,它就是只用这个函数的正弦响应结果得到了A、φ,所以书上的各种典型传函环节(惯性、振荡、一二阶微分、积分等)都是可以适用于观察频率特性得到的结果
自控1完结撒花**ヽ(°▽°)ノ*,已经是个精神自控人了
边栏推荐
- 判斷二叉樹是否為完全二叉樹
- PLC编程基础之数据类型、变量声明、全局变量和I/O映射(CODESYS篇 )
- Leecode learning notes
- 3D point cloud slam
- Judge whether the binary tree is a complete binary tree
- Marginal probability and conditional probability
- Spectrum analysis of ADC sampling sequence based on stm32
- Debian 10 installation configuration
- Southeast Asia e-commerce guide, how do sellers layout the Southeast Asia market?
- (4)UART应用设计及仿真验证2 —— RX模块设计(无状态机)
猜你喜欢
【原创】程序员团队管理的核心是什么?
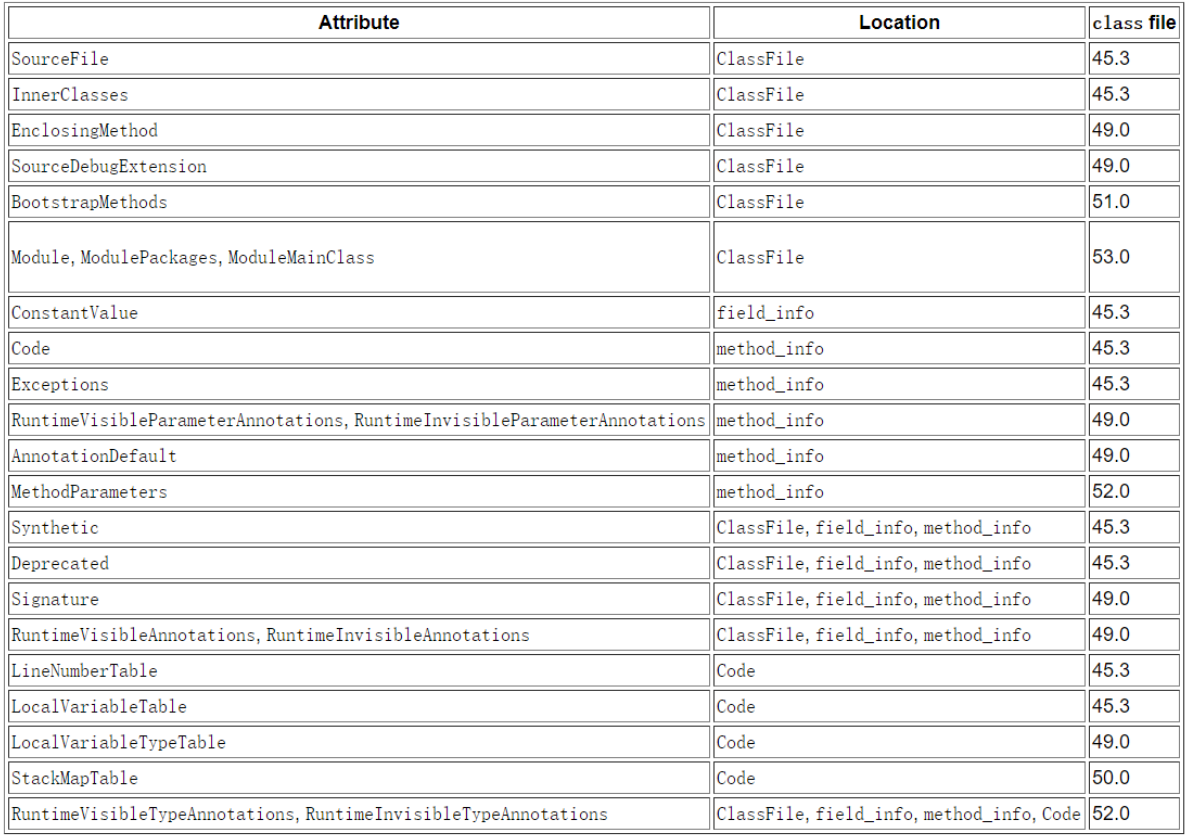
一文搞定class的微观结构和指令
一文搞定JVM的内存结构

SPSS analysis of employment problems of college graduates

Hainan Nuanshen tea recruits warmhearted people: recruitment of the product experience recommender of Nuanshen multi bubble honey orchid single cluster
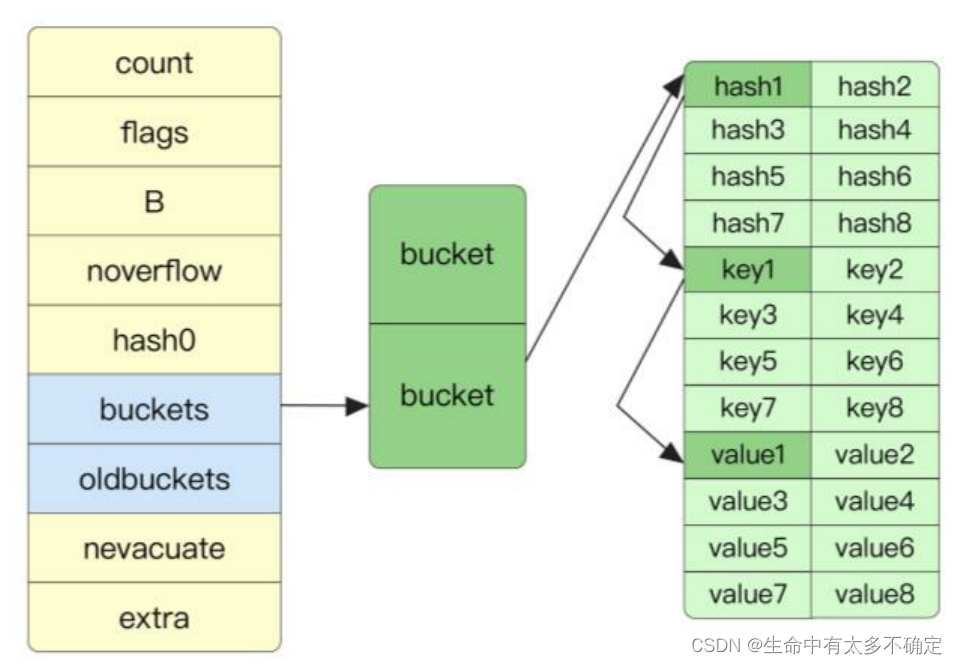
Go language implementation principle -- map implementation principle

如何快速理解复杂业务,系统思考问题?

Three.JS VR看房
From the perspective of quantitative genetics, why do you get the bride price when you get married

Three. JS VR house viewing
随机推荐
Nacos 的安装与服务的注册
Global and Chinese markets for welding products 2022-2028: Research Report on technology, participants, trends, market size and share
YML configuration, binding and injection, verification, unit of bean
Selenium+Pytest自动化测试框架实战
如何快速理解复杂业务,系统思考问题?
14种神笔记方法,只需选择1招,让你的学习和工作效率提高100倍!
Global and Chinese market of water treatment technology 2022-2028: Research Report on technology, participants, trends, market size and share
Getting started stm32--gpio (running lantern) (nanny level)
The method and principle of viewing the last modification time of the web page
regular expression
MoCo: Momentum Contrast for Unsupervised Visual Representation Learning
Leetcode daily question 1189 The maximum number of "balloons" simple simulation questions~
基于脉冲神经网络的物体检测
数据库基础知识(面试)
Global and Chinese markets of tantalum heat exchangers 2022-2028: Research Report on technology, participants, trends, market size and share
What is the process of building a website
Element operation and element waiting in Web Automation
Sum of two numbers, sum of three numbers (sort + double pointer)
LabVIEW打开PNG 图像正常而 Photoshop打开得到全黑的图像
Calculating the number of daffodils in C language
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-doVagqrR-1657012369280)(C:\Users\robinbird\AppData\Roaming\Typora\typora-user-images\image-20220420210012659.png)]](/img/b8/1fb921cc61d3d7fa78a648738b252b.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KrNrLKHm-1657012369284)(C:\Users\robinbird\AppData\Roaming\Typora\typora-user-images\image-20220420210717309.png)]](/img/01/eb90e5c3f6fdc64f721be991df9019.png)
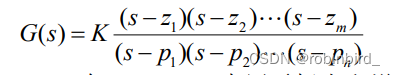
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-joecKule-1657012369287)(C:\Users\robinbird\AppData\Roaming\Typora\typora-user-images\image-20220420211133977.png)]](/img/24/ee7194792ce5515dc8333c9ed095f2.png)

![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-22Wx11XX-1657012369297)(C:\Users\robinbird\AppData\Roaming\Typora\typora-user-images\image-20220705111245340.png)]](/img/30/5e82f63df8860ba6ab997ac7111120.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-juj7D7RC-1657012369299)(C:\Users\robinbird\AppData\Roaming\Typora\typora-user-images\image-20220421100000555.png)]](/img/73/e040fd977aec3081b9d23a8e6dfaae.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ZF0zAQEi-1657012369301)(C:\Users\robinbird\AppData\Roaming\Typora\typora-user-images\image-20220705115014808.png)]](/img/ec/a8a894eb418c8ddbdc45f146784d73.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-N2SWPYb2-1657012369310)(C:\Users\robinbird\AppData\Roaming\Typora\typora-user-images\image-20220508110156814.png)]](/img/d3/adb265592247e13514e5e9841572e8.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ySVKe33P-1657012369310)(C:\Users\robinbird\AppData\Roaming\Typora\typora-user-images\image-20220508110214336.png)]](/img/f4/56d245c43d21542cafd052b861faf2.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WLfDF5oo-1657012369312)(C:\Users\robinbird\AppData\Roaming\Typora\typora-user-images\image-20220508110510079.png)]](/img/59/ef16fdd82bfb339fcca55b8ff13632.png)

![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-f2A0Bgbr-1657012369319)(C:\Users\robinbird\AppData\Roaming\Typora\typora-user-images\image-20220705161314080.png)]](/img/f1/4d9dc009701819f05ab6ab82dcd51b.png)