当前位置:网站首页>leetcode算法(1)
leetcode算法(1)
2020-11-09 12:58:00 【osc_tnexgcb8】
这是leetcode最简单的题了吧!!!
本次博主给大家推荐几个究极简单的算法, 简单归简单,但无论难易与否,万变不离其宗. 就由博主带大家从易到难,慢慢更新,积累. 如有更好的算法,还望大家分享.题目需求1:
小A 和 小B 在玩猜数字。小B 每次从 1, 2, 3 中随机选择一个,小A 每次也从 1, 2, 3 中选择一个猜。他们一共进行三次这个游戏,请返回 小A 猜对了几次?
输入的guess数组为 小A 每次的猜测,answer数组为 小B 每次的选择。guess和answer的长度都等于3。
代码实现
public class Solution {
public int game(int[] guess, int[] answer) {
int count = 0;
for (int i = 0; i < 3; i++) {
if (guess[i] == answer[i]){
count+=1;
}
}
return count;
}
public static void main(String[] args) {
Solution n2 = new Solution();
System.out.println(n2.game(new int[]{
1,2,3}, new int[]{
1, 2, 2}));
}
}
题目需求2:
求 1+2+...+n ,要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句(A?B:C)。
代码实现
public class Solution3 {
public int sumNums(int n) {
//等差数列求和
return (1+n)*n/2;
}
public static void main(String[] args) {
Solution3 q = new Solution3();
System.out.println(q.sumNums(3));
}
}
题目需求3:
给你一个正方形矩阵 mat,请你返回矩阵对角线元素的和。
请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。
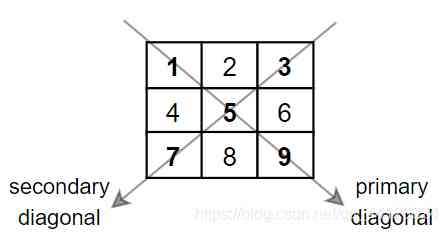
输出:1 + 5 + 9 + 3 + 7 = 25
注意,元素 mat[1][1] = 5 只会被计算一次。
代码实现
public class Solution4 {
int diagonal= 0;
public int diagonalSum(int[][] mat) {
for (int i=0;i<mat.length;i++){
for (int j = 0; j < mat[i].length; j++) {
if ( i==j || i+j == mat.length-1){
diagonal += mat[i][j];
}
}
}
return diagonal;
}
public static void main(String[] args) {
Solution4 s = new Solution4();
System.out.println(s.diagonalSum(new int[][]{
{
1,2,3},{
4,5,6},{
7,8,9}}));
}
}
题目需求4:
桌上有 n 堆力扣币,每堆的数量保存在数组 coins 中。我们每次可以选择任意一堆,拿走其中的一枚或者两枚,求拿完所有力扣币的最少次数。
简化前代码实现
public class Solution5 {
public int minCount(int[] coins) {
int count1 = 0;
int count2 = 0;
for (int i = 0; i < coins.length; i++) {
if (coins[i] % 2 ==0){
count1 += coins[i]/2;
}
if (coins[i] % 2 !=0){
count2 += coins[i]/2+1;
}
}
return count1+count2;
}
public static void main(String[] args) {
Solution5 s = new Solution5();
System.out.println(s.minCount(new int[]{
1,1,1}));
}
}
简化后代码实现
public class Solution5 {
public int minCount1(int[] coins) {
int c = 0;
for (int i = 0; i < coins.length; i++) {
c += coins[i] / 2;
c += coins[i] % 2;
}
return c;
}
public static void main(String[] args) {
Solution5 s = new Solution5();
System.out.println(s.minCount1(new int[]{
2,5,7}));
}
版权声明
本文为[osc_tnexgcb8]所创,转载请带上原文链接,感谢
https://my.oschina.net/u/4412486/blog/4709415
边栏推荐
- SQL statement to achieve the number of daffodils
- JVM learning (4) - garbage collector and memory allocation
- 块级元素和行内元素
- FGC online service troubleshooting, this is enough!
- Show profile analysis of SQL statement performance overhead
- Implement crud operation
- 在嵌入式设备中实现webrtc的第三种方式③
- pytorch加载语音类自定义数据集
- 深圳C1考证历程
- Setting up a proxy for the WGet command
猜你喜欢
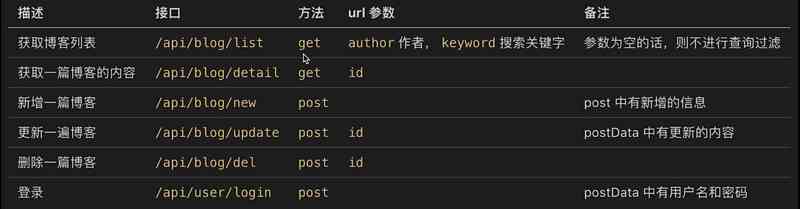
Learning notes of nodejs
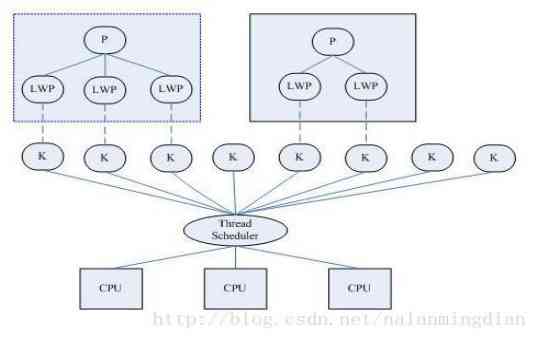
JVM学习(六)-内存模型和线程

Wechat circle

Android rights

在企业的降本增效诉求下,Cube如何助力科盾业务容器化“一步到位”?

The choice of domain name of foreign trade self built website
微信视频号播主排行榜2020年10月

Android架构之Navigation组件(二)
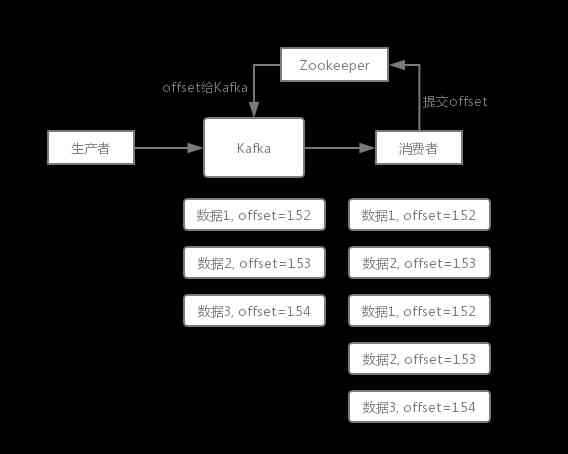
How to ensure that messages are not consumed repeatedly? (how to ensure the idempotent of message consumption)

FGC online service troubleshooting, this is enough!
随机推荐
A simple way to realize terminal text paste board
20201107第16课,使用Apache服务部署静态网站;使用Vsftpd服务传输文件
注意.NET Core进行请求转发问题
为wget命令设置代理
线上服务的FGC问题排查,看这篇就够了!
Tutorial system unity online course double 11 preferential registration is in progress
Tidb x micro banking reduces time consumption by 58%, and distributed architecture helps to realize inclusive finance
分库分表的 9种分布式主键ID 生成方案,挺全乎的
Interview summary on November 7, 2020 (interview 12K)
手写Koa.js源码
What are the implementations of distributed locks?
FGC online service troubleshooting, this is enough!
Depth analysis based on synchronized lock
块级元素和行内元素
苏宁基于知识图谱的大规模告警收敛和根因定位实践
Where should wild card SSL certificate register and apply
Using stream to read and write files to process large files
基于synchronized锁的深度解析
Show profile analysis of SQL statement performance overhead
Flink 系例 之 Reduce