当前位置:网站首页>Search (DFS and BFS)
Search (DFS and BFS)
2022-07-06 00:15:00 【rikka-l】
Search for
I was learning slope optimization DP... It turned out to be so hard , I gave up , First learn to search, relax (
BFS
Flood Fill Model
Flood Fill The model sounds like a cow , In fact, we have just learned search should have seen such a question , The Chinese name is flooding algorithm , Also called seed filling (Seed Fill), Used to determine the area connected to a given node in a multidimensional array . That may be more abstract , We'll know what it is after looking at the example .
Pond count
Topic link : Pond count
analysis : This problem is relatively simple , Let's start with the first row and the first column and search later , Found W when , Number of ponds ++, Then put it with this W All connected W Change it to .( Including this W Oneself ), The final number of ponds is the answer .
Code implementation :
#include<iostream>
#define x first
#define y second
using namespace std;
const int N=1010,M=N*N;
int n,m;
char g[N][N];
int ans;
typedef pair<int,int> PII;
PII q[M];
void bfs(int x,int y){
int hh=0,tt=-1;
q[++tt]={
x,y};
g[x][y]='.';
while(hh<=tt){
auto tmp=q[hh++];
int x1=tmp.x,y1=tmp.y;
for(int i=x1-1;i<=x1+1;i++){
for(int j=y1-1;j<=y1+1;j++){
if(i>=0&&i<n&&j>=0&&j<m&&g[i][j]=='W'){
g[i][j]='.';
q[++tt]={
i,j};
}
}
}
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=0;i<n;i++){
scanf("%s",g[i]);
}
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
if(g[i][j]=='W'){
bfs(i,j);
ans++;
}
}
}
printf("%d",ans);
return 0;
}
The castle problem
Topic link : The castle problem
analysis : For this question , Except for the required area, it is exactly the same as the above question , So we give bfs Just add a return value , For this wall, it means , We found that , If you decompose this number into binary , Suppose the lowest order is 0 position , The first 0 Is it 1 It means there is a west wall , The first 1 Is it 1 It means there is a north wall , The first 2 Is it 1 It means there is an east wall , The first 3 Is it 1 It means there is a south wall , We define the offset array in this order , It will be very convenient. .
Code implementation :
#include<iostream>
#define x first
#define y second
using namespace std;
typedef pair<int,int> PII;
int n,m;
const int N=55;
int d[4][2]={
{
0,-1},{
-1,0},{
0,1},{
1,0}};// The offset array is also defined in this order
int g[N][N];
int area,ans;
PII q[N*N];
bool vis[N][N];
int bfs(int sx,int sy){
// Return area
int area=0;
vis[sx][sy]=1;
int hh=0,tt=0;
q[0]={
sx,sy};
while(hh<=tt){
auto tmp=q[hh++];
area++;// Unity is added when leaving the team , No weight, no leakage
for(int i=0;i<4;i++){
int x=tmp.x+d[i][0],y=tmp.y+d[i][1];
if(x<0||x>=n||y<0||y>=m||vis[x][y]||g[tmp.first][tmp.second]>>i&1) continue;
q[++tt]={
x,y};
vis[x][y]=1;
}
}
return area;
}
int main(){
cin>>n>>m;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
cin>>g[i][j];
}
}
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
if(vis[i][j]) continue;
area=max(area,bfs(i,j));// Renewal area
ans++;
}
}
cout<<ans<<endl<<area;
return 0;
}
Mountains and valleys
Topic link : Mountains and valleys
analysis : This question is more interesting , And the above question ( It's too water ) Compared with some difficulty in thinking , In fact, when we search, we will find adjacent places with different heights , We set the same height as a connected block , We only need to pass two more when passing parameters bool Type variable has_lower and has_higher, If there is one higher than this connected block , Just put has_higher Set as true,has_lower Empathy , Then search and judge , If has_lower by false, It shows that there is nothing lower than this connected block , It means that the number of valleys should be ++,has_higher Empathy .
Code implementation :
#include<iostream>
#define x first
#define y second
using namespace std;
int n;
int peak,valley;
const int N=1010;
typedef pair<int,int> PII;
PII q[N*N];
int g[N][N];
bool vis[N][N];
int hh,tt;
void bfs(int x,int y,bool& has_higher,bool& has_lower){
vis[x][y]=1;
hh=tt=0;
q[0]={
x,y};
while(hh<=tt){
auto t=q[hh++];
int a=t.x,b=t.y;
for(int i=a-1;i<=a+1;i++){
for(int j=b-1;j<=b+1;j++){
if(i<1||i>n||j<1||j>n) continue;// Cross the border continue
if(g[i][j]>g[a][b]){
// If higher than it
has_higher=true;// Set as true
}
else if(g[i][j]<g[a][b]){
// If it is lower
has_lower=true;// Set as true
}
else if(!vis[i][j]){
// Or the same height but not searched , Just join the queue
vis[i][j]=1;
q[++tt]={
i,j};
}
}
}
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
scanf("%d",&g[i][j]);
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(vis[i][j]) continue;
bool has_higher=false,has_lower=false;
bfs(i,j,has_higher,has_lower);
// Because an area can be both a mountain and a valley , So it's very comfortable to write like this
if(!has_higher) peak++;
if(!has_lower) valley++;
}
}
cout<<peak<<" "<<valley;
return 0;
}
Shortest path model
The shortest path model is also a very common model , The difficulty should be low ...( I hope so ), We still learn through examples .
Maze problem
Topic link : Maze problem
analysis : Generally, find the shortest path with equal edge weights 、 The minimum number of operations can be used bfs To solve , This kind of question is too common , I won't explain it in detail . This question also needs to print the path , We just need to open another two-dimensional array , Just record the point from which each point is transferred , But in that case, it seems that we can only print from back to front ( Recursion can print from front to back ), Let's think from another angle , We let it go from the end to the beginning , This is equivalent , And when printing, you can directly print forward recursively .
Code implementation :
#include<iostream>
#include<cstring>
#define x first
#define y second
using namespace std;
typedef pair<int,int> PII;
int n;
const int N=1010;
int g[N][N];
PII pre[N][N];
PII q[N*N];
int d[4][2]={
{
1,0},{
-1,0},{
0,1},{
0,-1}};
void bfs(){
int hh=0,tt=0;
q[0]={
n-1,n-1};
while(hh<=tt){
auto t=q[hh++];
for(int i=0;i<4;i++){
int x=t.first+d[i][0],y=t.second+d[i][1];
if(x<0||x>=n||y<0||y>=n||pre[x][y].x!=-1||g[x][y]) continue;// Here, you can use it directly when you can't search back pre Array , Don't open another bool Array
q[++tt]={
x,y};
pre[x][y]=t;
}
}
}
int main(){
memset(pre,-1,sizeof pre);
scanf("%d",&n);
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
scanf("%d",&g[i][j]);
}
}
bfs();
PII ed(0,0);// from 0,0 Start printing
while(1){
printf("%d %d\n",ed.x,ed.y);
if(ed.x==n-1&&ed.y==n-1) break;// If you get to the end break
ed=pre[ed.x][ed.y];// Otherwise, find the previous point
}
return 0;
}
A warrior cow
Topic link : A warrior cow
analysis : named The Knight Of cattle , It reminds me of 《 Empty knight 》 This excellent game , In fact, there is no connection between the two , I just want to tell you the game of Amway . This question is essentially the same as the above question , It's just a different way of walking , Become a horse walking on the sun , The first place to go is the place that can be reached with the minimum number of steps .
Code implementation :
#include<iostream>
#include<cstring>
#define x first
#define y second
using namespace std;
typedef pair<int,int> PII;
int n,m;
const int N=160;
char g[N][N];
int dis[N][N];//dis[i][j] It means that the cow jumps to i,j The minimum number of steps required for this position
PII q[N*N];
int d[8][2]={
{
2,1},{
2,-1},{
1,2},{
1,-2},{
-1,2},{
-1,-2},{
-2,1},{
-2,-1}};//8 Seed walking method
int bfs(){
int ans=0;
int hh=0,tt=0;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
if(g[i][j]=='K'){
// find K The location of , And initialize the distance to 0
q[hh]={
i,j};
dis[i][j]=0;
break;
}
}
}
while(hh<=tt){
auto t=q[hh++];
for(int i=0;i<8;i++){
int x=t.x+d[i][0],y=t.y+d[i][1];
if(x<0||x>=n||y<0||y>=m||dis[x][y]!=-1||g[x][y]=='*') continue;
dis[x][y]=dis[t.x][t.y]+1;
q[++tt]={
x,y};
if(g[x][y]=='H') return dis[x][y];
}
}
}
int main(){
memset(dis,-1,sizeof dis);// First initialize all distances to -1, It also represents that this point has not been passed
cin>>m>>n;
for(int i=0;i<n;i++){
cin>>g[i];
}
cout<<bfs();
return 0;
}
Catch the cow
Topic link : Catch the cow
analysis : One dimensional coordinate bfs, It's a little bit easier , And here's a jump to 2*x Coordinate operation , If you are not sure, you can double the array , In fact, it opens 1 Double it , It must not be only The best solution , Think about it for yourself !
Code implementation :
#include<iostream>
#include<cstring>
using namespace std;
const int N=1e5+10;
int n,k,q[N],dis[N];//dis Record the distance , by -1 It means I haven't reached this point
int bfs(){
memset(dis,-1,sizeof dis);
q[0]={
n};
dis[n]=0;
int hh=0,tt=0;
while(hh<=tt){
auto t=q[hh++];
if(t==k) return dis[t];// It can be determined and returned when leaving the team , It can also be found in the following if Judgment in sentences , But then you have to write it three times , I compare lazy
if(t-1>=0&&dis[t-1]==-1){
dis[t-1]=dis[t]+1;
q[++tt]=t-1;
}
if(t+1<N&&dis[t+1]==-1){
dis[t+1]=dis[t]+1;
q[++tt]=t+1;
}
if(t*2<N&&dis[t*2]==-1){
dis[t*2]=dis[t]+1;
q[++tt]=2*t;
}
}
}
int main(){
cin>>n>>k;
cout<<bfs();
return 0;
}
Multi-source BFS
Multi-source BFS Is to search from multiple points , But it still ensures that the results of the first search are the smallest , It can solve some interesting problems .
Matrix distance
Topic link : Matrix distance
analysis : We just need to set all the values to 1 Join the queue at , And then from these 1 set out , You can find the shortest Manhattan distance at each point of the road .
Code implementation :
#include<iostream>
#define x first
#define y second
using namespace std;
typedef pair<int,int> PII;
const int N=1010;
int n,m,g[N][N],hh=0,tt=-1,d[4][2]={
{
1,0},{
-1,0},{
0,1},{
0,-1}};
PII q[N*N];
bool vis[N][N];
void bfs(){
while(hh<=tt){
auto t=q[hh++];
for(int i=0;i<4;i++){
int x=t.x+d[i][0],y=t.y+d[i][1];
if(x<1||x>n||y<1||y>m||vis[x][y]) continue;
vis[x][y]=1;
g[x][y]=g[t.x][t.y]+1;
q[++tt]={
x,y};
}
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
scanf("%1d",&g[i][j]);
if(g[i][j]==1){
// For 1 The point of
q[++tt]={
i,j};// Join the queue
g[i][j]=0;// The value assigned to 0
vis[i][j]=1;// Marked as searched
}
}
}
bfs();
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
printf("%d ",g[i][j]);
}
puts("");
}
return 0;
}
Minimum step model
Except for the shortest way to walk , We can still use it bfs Find the minimum number of operation steps to reach a certain state , This topic often has routines , Relatively simple ( The difficulty is pruning ).
Magic board
Topic link : Magic board
analysis : Let's find the sequence of operations with the smallest dictionary order , Then we should give priority to A operation , Next use B operation , Last use C operation , The result must be the smallest dictionary order . But this question is really disgusting , It's all about dealing with some details , Look at the detailed comments of the code .
Code implementation :
#include<iostream>
#include<unordered_map>
#include<queue>
using namespace std;
unordered_map<string,int> dis;//dis Record the number of operation steps corresponding to each string
unordered_map<string,pair<char,string>> pre;//pre Record which string is converted by which operation
string str,ed;
char g[2][4];//g Arrays are used to perform correlation transformations
void print(string tmp){
if(tmp==str) return ;
print(pre[tmp].second);
cout<<pre[tmp].first;
}
void set(string tmp){
for(int i=0;i<4;i++){
g[0][i]=tmp[i];
}
for(int i=7;i>3;i--){
g[1][7-i]=tmp[i];
}
}
string get(){
string ans;
for(int i=0;i<4;i++){
ans+=g[0][i];
}
for(int i=3;i>-1;i--){
ans+=g[1][i];
}
return ans;
}
string move0(string tmp){
//A Transformation method
set(tmp);// take tmp The string is split into g Array , Carry out relevant operations , The following functions are the same
for(int i=0;i<4;i++) swap(g[0][i],g[1][i]);
return get();// After the execution , take g The status in is spelled into a string and returned
}
string move1(string tmp){
//B Transformation method
set(tmp);
char a=g[0][3],b=g[1][3];
for(int i=2;i>=0;i--){
g[0][i+1]=g[0][i];
g[1][i+1]=g[1][i];
}
g[0][0]=a,g[1][0]=b;
return get();
}
string move2(string tmp){
//C Transformation method
set(tmp);
char a=g[0][1];
g[0][1]=g[1][1];
g[1][1]=g[1][2];
g[1][2]=g[0][2];
g[0][2]=a;
return get();
}
int bfs(string str,string ed){
if(str==ed){
return 0;
}
queue<string> q;
q.push(str);
dis[str]=0;
while(q.size()){
auto t=q.front();
q.pop();
string m[3];// Record three converted strings
m[0]=move0(t);
m[1]=move1(t);
m[2]=move2(t);
for(int i=0;i<3;i++){
if(!dis[m[i]]){
// First transition to this state
dis[m[i]]=dis[t]+1;
pre[m[i]]={
'A'+i,t};
q.push(m[i]);
if(m[i]==ed) return dis[ed];// If completed , Go back now
}
}
}
}
int main(){
int x;
for(int i=0;i<8;i++){
cin>>x;
ed+=x+'0';// Target state
}
str="12345678";// Starting state
cout<<bfs(str,ed)<<endl;
print(ed);// Recursive printing
return 0;
}
Double ended queue wide search
For a distance only 0 and 1 How to walk , We can find the shortest path by double ended queue search , If the distance is 0, The new state is inserted from the head of the queue , Otherwise, insert from the tail , Because a point may be out of the team twice , But only the shortest updated value is correct , Therefore, we only judge whether it has been searched when counting out of the queue , The final answer is also correct .
Circuit maintenance
Topic link : Circuit maintenance
analysis : Pictured , Let's set the coordinates of the point like this , We can easily get , Only points with even horizontal and vertical coordinates can be reached , Because the change of the sum of the horizontal and vertical coordinates along the oblique line is even , And the sum of the horizontal and vertical coordinates of the starting point is also even . The left side of the grid is represented by the lower right corner of the grid , The red ones in the picture are grid coordinates , The blue ones are point coordinates .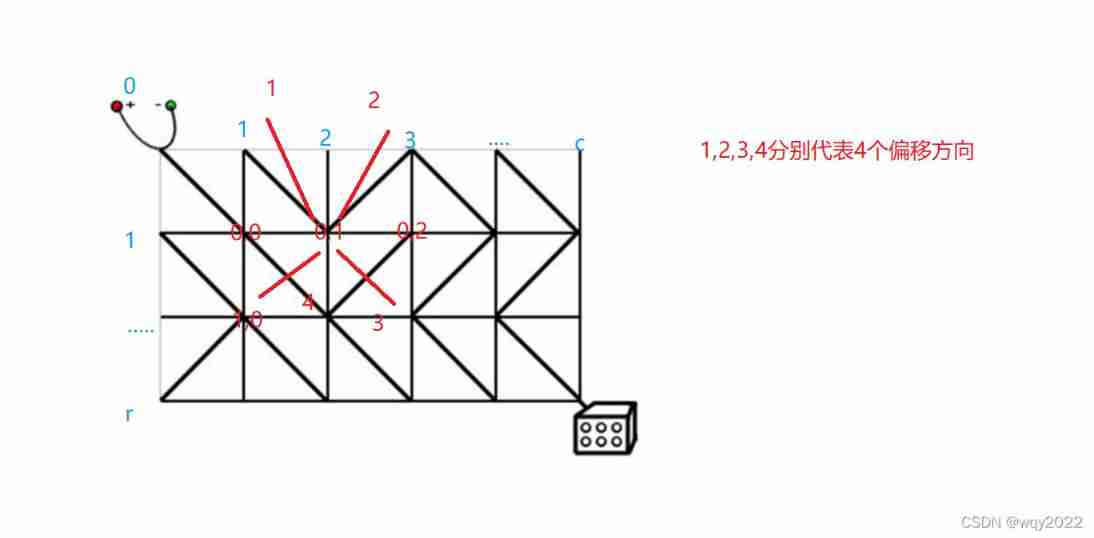
in addition , For the change of grid coordinates , If we record in another array , It's easier to write the final answer ( Just follow the routine of double ended queue search ).
Code implementation :
#include<iostream>
#include<cstring>
#include<deque>
using namespace std;
int r, c;
const int N = 510;
char g[N][N];
int dis[N][N];//dis[i][j] Express i,j To 0,0 Minimum number of operation steps
bool vis[N][N];
int d[4][2] = {
{
-1,-1},{
-1,1},{
1,1},{
1,-1} };// Follow the left change of four oblique lines , It's the top left , The upper right , The lower right , The lower left
int s[4][2] = {
{
-1,-1},{
-1,0},{
0,0},{
0,-1} };//s Is the change of coordinate points along the four oblique lines , Note the correspondence with the above , You can set a point to simulate this , You can exit the corresponding changes
char check[5] = "\\/\\/";// because \ Often used to escape characters , Therefore, we should express \ Need to be written \\ such , Also pay attention to keep consistent with the above direction
void bfs() {
memset(dis, 0x3f, sizeof dis);// Initialize to a large number
memset(vis, 0, sizeof vis);
dis[0][0] = 0;// The starting point is initialized to 0
deque<pair<int, int>> q;
q.push_back({
0,0 });
while (q.size()) {
auto t = q.front();
q.pop_front();
if (vis[t.first][t.second]) continue;// If updated , You can't update it anymore
vis[t.first][t.second] = 1;
for (int i = 0; i < 4; i++) {
int x = t.first + d[i][0], y = t.second + d[i][1];// Coordinates of the arrival point
if (x<0 || x>r || y<0 || y>c) continue;
int a = t.first + s[i][0], b = t.second + s[i][1];// The left side of the grid , It is mainly used to compare whether the diagonal direction is consistent
int tmp = dis[t.first][t.second] + (check[i] != g[a][b]);// The inconsistent distance is +1
if (tmp < dis[x][y]) {
// If the distance is less than the current distance , to update
dis[x][y] = tmp;
if (g[a][b] != check[i]) q.push_back({
x,y });// If the direction is inconsistent , It shows that an extra distance is used , Add it to the end of the team
else q.push_front({
x,y });// Otherwise, it will be added to the head of the team
}
}
}
}
int main() {
int T;
scanf("%d", &T);
while (T--) {
scanf("%d%d", &r, &c);
for (int i = 0; i < r; i++) {
scanf("%s", g[i]);// We use the lower right corner of each square to represent the left corner of this square
}
if ((r + c) % 2) puts("NO SOLUTION");// If it's odd , unsolvable
else {
bfs();
printf("%d\n", dis[r][c]);// from 0,0 Point to r,c The shortest distance of a point
}
}
return 0;
}
Two way search
What is this ? Let's look at the example first , From the limitations of plain search to solve the problem, we can extract two-way wide search .
String transformation
Topic link : String transformation
analysis : In this question , We can search directly and violently , The maximum string length is 20, And at most 6 Medium transformation mode , Suppose every character can be transformed , Then the number of states of each extended layer will expand 120 times , There is no doubt that TLE/MLE Of , The reason is that each extension layer , The number of states changes too much . In this problem, we found that the method of searching from the starting point to the end seems to fail , But let's think again , We can search the middle from the beginning and the end at the same time , This is the expansion in two directions 120 Times, but the number of expansion becomes half of the original , Wonderful ! But we should also pay attention to ( Not in this question , But you may encounter ), It is possible that the expansion speed of the search from the starting point is much faster than that from the end point , Then we need to search more from the end , Don't search from the starting point , A better way is to search whichever state has a small number , This is also an optimization , See code for details .
Code implementation :
#include<iostream>
#include<unordered_map>
#include<queue>
using namespace std;
const int N=6;
int n;
string a[N],b[N];
unordered_map<string,int> da,db;// Record the number of operation steps to each string with a hash table ,da Record from the starting point to ,db Record from the end to
queue<string> qa,qb;//qa Store those searched from the starting point ,qb Store the search from the destination
string str,ed;
// Note that the reference to the array is written as string(&a)[N]
int extend(queue<string> &q,unordered_map<string,int>&da,unordered_map<string,int>&db,string(&a)[N],string(&b)[N]){
// Only extend one layer
int d=da[q.front()];
while(q.size()&&da[q.front()]==d){
// Ensure that only one layer is extended
auto t=q.front();
q.pop();
for(int i=0;i<n;i++)// consider n Medium transformation method
for(int j=0;j<t.size();j++)// Not here kmp 了 , Anyway, the data range is very small
if(t.substr(j,a[i].size())==a[i]){
string ans=t.substr(0,j)+b[i]+t.substr(j+a[i].size());// Replaced string
if(da.count(ans)) continue;// If it has been updated, it will not be updated , Only in this way can we ensure the shortest
da[ans]=da[t]+1;
if(db.count(ans)) return da[ans]+db[ans];// If both sides are found , Return the sum of distances
q.push(ans);
}
}
return 11;// Otherwise, a value greater than... Is returned 10 Number of numbers
}
int bfs(){
if(str==ed) return 0;
qa.push(str);
qb.push(ed);
da[str]=db[ed]=0;
int step=0;
while(qa.size()&&qb.size()){
// As long as one is empty, it means it is impossible
int t=0;
if(qa.size()<=qb.size()) t=extend(qa,da,db,a,b);// use qa Expand
else t=extend(qb,db,da,b,a);// use qb Expand , Note that the extension from the end point is from b To a, The hash table position should also be reversed
if(t<=10) return t;
if(++step==10) return 11;// If it has arrived 10 I haven't found the answer yet , return 11( Any one greater than 10 Number of numbers )
}
return 11;// I didn't find it after searching , return 11
}
int main(){
cin>>str>>ed;
while(cin>>a[n]>>b[n]) n++;// The title does not give us a specific number of transformation schemes , We write like this
int ans=bfs();
if(ans>10) puts("NO ANSWER!");
else cout<<ans<<endl;
return 0;
}
A*
A* What does algorithm mean ? Let's consider some problems first , For example, the eight digit problem , There are many states in our direct violent search , Are there any methods we can optimize ? It's here A* Algorithm , We give each state an estimate of its distance to the end point according to a certain calculation method ( If this estimate is satisfied, it must be less than or equal to the true distance to ensure its correctness ), Then we take the minimum sum of the true value to the origin and the estimated value to the destination in the queue every time to expand , When the finish line goes out , Its true value to the origin must be the smallest .( Assumption is not the smallest , Then there must be a point with a smaller real distance to the origin and an estimated distance to the endpoint , Because the estimated distance to the destination is less than or equal to the actual distance , This end will not be out of the queue ). If we calculate in this way, we will traverse a lot less States , So it's a good optimization . in addition , If The problem is unsolved Words , use A * The algorithm will More slowly , in addition , Using this algorithm is Negative weighted edges are allowed Of , but No negative weight ring . therefore , Our problem is to design a function to calculate the estimated distance to the destination , Many times, we don't need to design it ourselves , Because what we get is basically what our predecessors have created , We need to understand the functions designed by predecessors , At the same time, it will also inspire us to design our own functions . One other thing , This method can only ensure that the value of the end point when leaving the queue is the minimum , Nothing else .
give an example : The edge weights in the figure are 1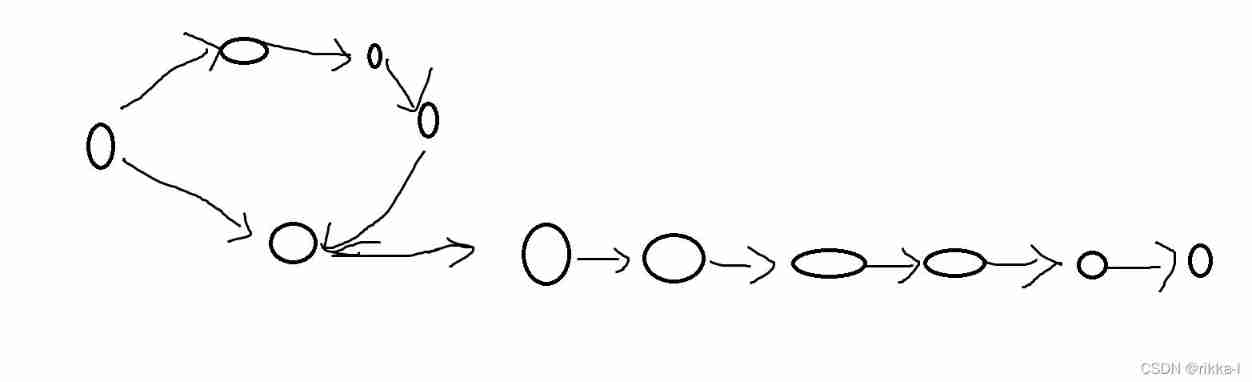
The degree of 0 The point of is the starting point , The degree of 0 The point of is the end . Try it on your own .
Eight digital
Topic link : Eight digital
Tips : This question can also be written by two-way search .
analysis : Two questions , One 、 We need to find A function is given to calculate the estimated distance from a certain state to the end state, and the estimated distance is less than the real distance , For this question , Let's compare the current state and the end state 3*3 Lattice of , Add the Hamiltonian distance from each point of the current state to the position it should be to , It is such an estimated distance , Because if you want to move the point, you must let x Exchange with it , For each point, the minimum commutative Hamiltonian distance times , So this function is feasible .
Two 、 Judge whether there is a solution , This 《 Advanced guide to algorithm competition 》 It is said that , We put 3*3 The matrix of forms a row , So the end “12345678x” in 0 In reverse order ( Ignore x), We found that , When we let x Exchange with elements on the same line , The number of reverse pairs does not change , Exchange with the following elements above , In reverse order, the quantity is either +2, or -2, Or not , Therefore, our initial state has an even number of pairs, which are in reverse order and have a solution ! actually , For all odd numbers * This is true for odd numbers of such problems , And for even numbers * The problem of even numbers , Only when the parity of the reverse order pair is in two states x Only when the parity of the difference in the number of rows is the same can there be a solution ( Those who are interested can deduce by themselves ), And the above just proves the necessity , The sufficiency has not been proved , It is difficult to prove the sufficiency , There's not much here bb 了 ( I won't ).
Code implementation :( More details ,100ms, It's pretty fast )
#include<iostream>
#include<unordered_map>
#include<algorithm>
#include<queue>
using namespace std;
typedef pair<int,string> PIS;
unordered_map<string,int> dist;// Record the distance to each string
unordered_map<string,pair<char,string>> pre;// Record the previous string of each string and the operation
int d[4][2]={
{
-1,0},{
0,-1},{
1,0},{
0,1}};// Top left bottom right
char s[4]={
'u','l','d','r'};// Correspond well 4 A direction
int g(string str){
// Find out g The estimated value of the state to the end
int res=0;
for(int i=0;i<str.size();i++)
if(str[i]!='x'){
int t=str[i]-'1';
res+=abs(i/3-t/3)+abs(i%3-t%3);
}
return res;
}
void astar(string str){
string ed="12345678x";
dist[str]=0;
priority_queue<PIS,vector<PIS>,greater<PIS>> heap;// A string that stores the sum of the true distance to the starting point and the estimated distance to the end point
heap.push({
g(str),str});
while(heap.size()){
auto t=heap.top();
heap.pop();
string state=t.second;
if(state==ed) break;// At the end break
int step=dist[state];// Record the steps to the present
int x,y;
for(int i=0;i<state.size();i++)
if(state[i]=='x'){
x=i/3,y=i%3;
break;
}
string sour=state;// Make a backup , The next step is to use
for(int i=0;i<4;i++){
// Switch in four directions
int a=x+d[i][0],b=y+d[i][1];
if(a>=0&&a<3&&b>=0&&b<3){
swap(state[x*3+y],state[a*3+b]);
if(!dist.count(state)||dist[state]>step+1){
// If this state has not been searched or the current search distance is smaller
dist[state]=step+1;// Update distance
pre[state]={
s[i],sour};// Record the precursor
heap.push({
dist[state]+g(state),state});// Add to the heap
}
swap(state[x*3+y],state[a*3+b]);// Restore the scene
}
}
}
string res;// Store answers
while(ed!=str){
res+=pre[ed].first;
ed=pre[ed].second;
}
reverse(res.begin(),res.end());// Because it is pushed backwards , If you are exporting, you need to reverse
cout<<res;
}
int main(){
string str,s;
for(int i=0;i<9;i++){
string tmp;
cin>>tmp;
if(tmp!="x") s+=tmp;
str+=tmp;
}
int cnt=0;
for(int i=0;i<8;i++)// Find the number of pairs in reverse order
for(int j=i+1;j<8;j++)
if(s[i]>s[j]) cnt++;
if(cnt%2) cout<<"unsolvable";
else astar(str);
return 0;
}
The first k A short circuit
Topic link : The first k A short circuit
analysis : Continue to think from above , The first time out of the line at the end is the shortest , The first k Will it be the first time out of the team k Short circuit ? The answer is right , The proof is similar to the above , I won't go into that , For this problem, we need to estimate the distance to the destination , Let's run directly in the opposite direction dijkstra The algorithm finds the shortest distance from all points to the end , And this shortest distance must be less than or equal to the real number 2~k short distance , So it's right .
Code implementation :
#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
const int N=1010,M=2e4+10;// Reverse side building requires twice the number of sides
typedef pair<int,int> PII;
typedef pair<int,PII> PIII;
int dist[N],h[N],rh[N],idx=1,e[M],ne[M],w[M];//rh It is the head node of reverse edge construction
int n,m,S,T,K,a,b,c,cnt;
bool st[N];
void add(int* h,int a,int b,int c){
e[idx]=b,ne[idx]=h[a],w[idx]=c,h[a]=idx++;
}
void dijkstra(){
priority_queue<PII,vector<PII>,greater<PII>> heap;
memset(dist,0x3f,sizeof dist);
dist[T]=0;
heap.push({
0,T});
while(heap.size()){
auto t=heap.top();
heap.pop();
int u=t.second;
if(st[u]) continue;
st[u]=1;
for(int i=rh[u];i;i=ne[i]){
int j=e[i];
if(dist[j]>dist[u]+w[i]){
dist[j]=dist[u]+w[i];
heap.push({
dist[j],j});
}
}
}
}
int astar(){
priority_queue<PIII,vector<PIII>,greater<PIII>> heap;
heap.push({
dist[S],{
0,S}});// Namely { The sum of the true value to the starting point and the estimated value to the end ,{ The true value to the starting point , Number }}
if(dist[S]==0x3f3f3f3f) return -1;// It's a special verdict S And T Disconnected situation
while(heap.size()){
auto t=heap.top();
heap.pop();
int u=t.second.second,dis=t.second.first;
if(u==T) cnt++;
if(cnt==K) return dis;
for(int i=h[u];i;i=ne[i]){
int j=e[i];
heap.push({
dis+w[i]+dist[j],{
dis+w[i],j}});
}
}
return -1;// This node cannot be accessed K Time
}
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
cin>>a>>b>>c;
add(h,a,b,c);
add(rh,b,a,c);// Reverse side building
}
cin>>S>>T>>K;
if(S==T) K++;// If the starting and ending points are the same ,0 Will be counted as the shortest , But we don't have this way , So ask k+1 A short circuit
dijkstra();// Run in the opposite direction dijkstra
cout<<astar();
return 0;
}
DFS
DFS And connectivity model
maze
Topic link : maze
This question uses bfs Can also do , Here we use dfs To achieve , Be careful : Search each point in this question only once , Therefore, there will be no recovery of the site , in addition , here dfs Can't ask for the shortest circuit , Only connectivity can be found . however dfs The code of is shorter , Better writing .
Code implementation :
#include <cstring>
#include <iostream>
using namespace std;
const int N = 110;
int n;
char g[N][N];
int sx, sy, ex, ey;//sx,sy Is the starting point coordinate ,ex,ey Is the end point coordinate
int dx[4] = {
-1, 0, 1, 0 }, dy[4] = {
0, 1, 0, -1 };
bool st[N][N];
bool dfs(int x, int y) {
if (g[x][y] == '#') return false;
if (x == ex && y == ey) return true;
st[x][y] = true;
for (int i = 0; i < 4; i++) {
int a = x + dx[i], b = y + dy[i];
if (a < 0 || a >= n || b < 0 || b >= n) continue;
if (st[a][b]) continue;
if (dfs(a, b)) return true;
}
return false;
}
int main() {
int T;
cin >> T;
while (T--) {
cin >> n;
for (int i = 0; i < n; i++) cin >> g[i];
cin >> sx >> sy >> ex >> ey;
memset(st, 0, sizeof st);
if (dfs(sx, sy)) puts("YES");
else puts("NO");
}
return 0;
}
Red and black
Topic link : Red and black
This question can also pass bfs solve , But it's still that ,dfs The code is short , Here we use global variables to record the number , Pay attention to a very stupid point in this question , First read into the column , Read again and enter the profession .
Code implementation :
#include <cstring>
#include <iostream>
using namespace std;
const int N = 25;
int n, m;
char g[N][N];
bool st[N][N];
int dx[4] = {
-1, 0, 1, 0 }, dy[4] = {
0, 1, 0, -1 };
int cnt;
void dfs(int x, int y) {
cnt++;
st[x][y] = true;
for (int i = 0; i < 4; i++) {
int a = x + dx[i], b = y + dy[i];
if (a < 0 || a >= n || b < 0 || b >= m) continue;
if (g[a][b] != '.') continue;
if (st[a][b]) continue;
dfs(a, b);
}
}
int main() {
while (cin >> m >> n, n || m) {
cnt = 0;// Remember 0
for (int i = 0; i < n; i++) cin >> g[i];
int x, y;
for (int i = 0; i < n; i++)// Find the starting position
for (int j = 0; j < m; j++)
if (g[i][j] == '@') {
x = i;
y = j;
}
memset(st, 0, sizeof st);
dfs(x, y);
cout << cnt << endl;
}
return 0;
}
DFS And search order
I don't know the main characteristics of these questions , However, writing these questions can lay the foundation for the later pruning optimization .
Horse walking day
Topic link : Horse walking day
This question is obviously not difficult , We only need to pass an additional parameter to indicate the number of points currently found during the deep search , When points are compared with n*m When equal ,ans++, You can find the final answer .
Code implementation :
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 10;
int n, m;
bool st[N][N];
int ans;
int dx[8] = {
-2, -1, 1, 2, 2, 1, -1, -2};
int dy[8] = {
1, 2, 2, 1, -1, -2, -2, -1};
void dfs(int x, int y, int cnt){
if (cnt == n * m){
ans ++ ;
return;
}
st[x][y] = true;
for (int i = 0; i < 8; i ++ ){
int a = x + dx[i], b = y + dy[i];
if (a < 0 || a >= n || b < 0 || b >= m) continue;
if (st[a][b]) continue;
dfs(a, b, cnt + 1);
}
st[x][y] = false;// Don't forget to restore the scene here
}
int main(){
int T;
scanf("%d", &T);
while (T -- ){
int x, y;
scanf("%d%d%d%d", &n, &m, &x, &y);
memset(st, 0, sizeof st);
ans = 0;
dfs(x, y, 1);
printf("%d\n", ans);
}
return 0;
}
The word chain
Topic link : The word chain
analysis : Let's just pop it up , For two strings that can be connected , We certainly hope that the less overlap the better , Only in this way can the connection be longer , So we can start searching .
Code implementation :
#include <iostream>
using namespace std;
const int N = 21;
int n;
string word[N];
int g[N][N];//g[i][j] It means the first one i The prefix of a string and the j Maximum coincidence length of suffixes of strings
int used[N];
int ans;
void dfs(string dragon, int last){
//
ans = max((int)dragon.size(), ans);// Update answers ,max Only two of the same type can be compared , So the size_t Convert to int
used[last] ++ ;//last Times used ++
for (int i = 0; i < n; i ++ )
if (g[last][i] && used[i] < 2)// Both must have common length and i Used less than 2 Time
dfs(dragon + word[i].substr(g[last][i]), i);// Direct splicing i Starting from the subscript of the overlap length, the next part
used[last] -- ;// Restore the scene
}
int main(){
cin >> n;
for (int i = 0; i < n; i ++ ) cin >> word[i];
char start;
cin >> start;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ ){
string a = word[i], b = word[j];
for (int k = 1; k < min(a.size(), b.size()); k ++ )// Enumerate common lengths , Can't get a or b The length of
if (a.substr(a.size() - k, k) == b.substr(0, k)){
// Enumerate from small to large
g[i][j] = k;//
break;// Once found break, This is the smallest
}
}
for (int i = 0; i < n; i ++ )
if (word[i][0] == start)// Search only after receiving the initial letter
dfs(word[i], i);
cout << ans << endl;// Output the answer
return 0;
}
Divide into prime arrays
Topic link : Divide into prime arrays
analysis : For this question , Just pop up . That is, consider how to put each number in order .
Code implementation :
#include <iostream>
#include <vector>
using namespace std;
const int N = 10;
int n, a[N], ans = N, len;
int gcd(int x, int y) {
// Find the greatest common divisor
return y ? gcd(y, x % y) : x;
}
vector<int> g[N];//g[i] It means the first one i Number of groups
bool check(int u, int c) {
// Check u Can I put c In the group
for (int i = 0; i < g[c].size(); i++)
if(gcd(g[c][i], u) > 1) return false;
return true;
}
void dfs(int u) {
if(len >= ans) return;// Add a pruning optimization
if(u == n) {
// If you finish thinking n Number , Just update the answer
ans = min(ans, len);
return;
}
for(int i = 0; i < len; i++) {
// Consider all groups that currently exist
if(check(a[u], i)) {
// Consider whether you can put
g[i].push_back(a[u]);
dfs(u + 1);
g[i].pop_back();// Restore the scene
}
}
g[len++].push_back(a[u]);// Put into a new group
dfs(u + 1);
g[--len].pop_back();// Restore the scene
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++) scanf("%d", a + i);
dfs(0);
printf("%d\n", ans);
}
DFS And pruning and optimization
We know : For many questions , If we search directly, there are many states , At this time, we can greatly reduce the time complexity through appropriate pruning and optimization , But we can't calculate the time complexity . Generally speaking , Common optimization and pruning strategies are as follows :
- Optimize search order
Search in different order , The time we spend may be different , The focus of this optimization is to let us find a faster search order . - Eliminate equivalent redundancy
This is easier to understand , For example, solve combinatorial problems , If we enumerate the ordinal number, we will enumerate a state many times , At this time, enumerating combinators will greatly optimize time . - Feasibility pruning
seeing the name of a thing one thinks of its function , When we find that a certain state is no longer satisfactory , Just terminate - Optimal pruning
The current policy cannot update the answer , Directly to terminate - Memorize ( We are mainly in dp As mentioned in , I won't focus on it here )
Kittens climb mountains
Topic link : Kittens climb mountains
analysis : Obviously , For this problem, we just need to enumerate which car each kitten is in , But the number of States is still very large , So we need to prune and optimize , See code for relevant contents .
Code implementation :
So I ran away 20ms about , It's still very fast .
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
#define x first
#define y second
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int N=20;
int sum[N],w[N],n,tot,ans;
void dfs(int x,int y){
//y Number of representative cars
if(y>=ans) return ;// If the current number of cars is greater than or equal to ans, There is no need to search
if(x==n) {
// That's it n Items , because y>=ans The situation has been cut , So it can be updated here
ans=y;
return ;
}
for(int i=0;i<y;i++)// Before consideration y A car , That is to say 0~y-1 A car
if(sum[i]+w[x]<=tot){
sum[i]+=w[x];// Put in the i A car
dfs(x+1,y);// Consider the next item
sum[i]-=w[x];// Restore the scene
}
sum[y]=w[x];// Put in the y A car
dfs(x+1,y+1);// The number of cars ++, Consider the next item
sum[y]=0;// Restore the scene
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n>>tot;
ans=n;
for(int i=0;i<n;i++) cin>>w[i];
sort(w,w+n,greater<int>());// Sort from large to small , Because the number of searches for heavy cats is certainly less than that for small cats
dfs(0,0);// Consider the i A cat , Put in the j A car
cout<<ans<<endl;
return 0;
}
Sudoku
Topic link : Sudoku
analysis : It's still an interesting question , Don't write Sudoku by yourself in the future , In fact, it's easy to search directly , But we must consider optimization , Otherwise, it's bound to TLE, All the details about optimization are in the code .
Code implementation :
#include<iostream>
using namespace std;
const int N=9,M=1<<N;
char num[100];
int map[M];//map[i] The value of is based on two i The logarithmic
int cnt[M];//cnt[i] Storage i In the binary representation of 1 The number of
int row[N],col[N],cell[3][3];//row,col,cell Each line is represented by a binary number 、 A column of 、 The state of a Jiugongge , The second is binary i Position as 1 On behalf of i Optional , Suppose that from right to left, there are 1、2、3…… position
void draw(int x,int y,int n,bool is_set){
//is_set by true When the x,y The character of the corresponding position is set to '1'+n, by false The position should be '.', And update the row,col,cell The state of the array
if(is_set) num[x*N+y]='1'+n;
else num[x*N+y]='.';
int v=1<<n;
if(!is_set) v=-v;// If yes, change to . Words , Then the state should be added v, Because the number of this position can be selected again
row[x]-=v;
col[y]-=v;
cell[x/3][y/3]-=v;//x/3 and y/3 Corresponding to the abscissa and ordinate of the Jiugong lattice respectively
}
void init(){
// At the beginning, every number can be used
for(int i=0;i<N;i++) row[i]=col[i]=(1<<N)-1;
for(int i=0;i<3;i++)
for(int j=0;j<3;j++)
cell[i][j]=(1<<N)-1;
}
int lowbit(int x){
// Find the lowest one 1
return x&-x;
}
int get(int x,int y){
return row[x]&col[y]&cell[x/3][y/3];// Returns three numbers & The value after , One of the returned digits is 1, It means that this number is optional
}
bool dfs(int c){
if(!c) return true;// Found the answer
// Find the place with the least number of entries
int minc=10;
int x,y;
for(int i=0;i<N;i++)
for(int j=0;j<N;j++)
if(num[i*N+j]=='.'){
int tmp=get(i,j);
if(cnt[tmp]<minc){
minc=cnt[tmp];
x=i,y=j;
}
}
int tmp=get(x,y);
for(int i=tmp;i;i-=lowbit(i)){
int t=map[lowbit(i)];// Find out how many you can fill
draw(x,y,t,true);// Fill in the
if(dfs(c-1)) return true;// This ensures that once the answer is found , Will return layer by layer , end dfs
draw(x,y,t,false);// Get rid of
}
return false;// No answer found
}
int main(){
for(int i=0;i<N;i++) map[1<<i]=i;
for(int i=0;i<1<<N;i++)
for(int j=0;j<N;j++)
cnt[i]+=i>>j&1;
while(cin>>num,num[0]!='e'){
init();
int s=0;// Record . The number of
for(int i=0;i<N;i++)
for(int j=0;j<N;j++)
if(num[i*N+j]=='.') s++;
else{
int t=num[i*N+j]-'1';// Alphabet character 1~9 Convert to number 0~8
draw(i,j,t,true);// call draw function
}
dfs(s);// Search for
puts(num);// Output num Array
}
return 0;
}
stick
Through the study of the previous questions , We found that pruning and optimization of search is really not a very simple problem , The same is true for this problem .
Topic link : stick
analysis : It's easy to think of pop search , We directly consider how to prune , See code for details .
Code implementation :
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=64;
int n,w[N],sum,str,len;//sum Indicates total length
bool st[N];// Record whether each point has been enumerated
// Because we may have both enumerations 1,3,2, Enumerate again 1,2,3 The situation of , Therefore, we enumerate from front to back in order to ensure that only combinators are enumerated
bool dfs(int u,int len,int x){
// Considering the u Group , The current length is len, From x Start enumerating numbers
if(u*str==sum) return true;// Satisfaction is over
if(len==str) return dfs(u+1,0,0);// If this set of enumerations is completed , Just continue with the following enumeration
for(int i=x;i<n;i++){
if(st[i]||w[i]+len>str) continue;// Joined or can't join
st[i]=1;
if(dfs(u,w[i]+len,i+1)) return true;
st[i]=0;// Restore the scene
if(!len||w[i]+len==str) return false;
/* This means that if this stick is the first or last one in this group, but there is no solution Suppose there is a legal scheme behind this branch , Then this number will be in the following group If the number is in the first position in the Group , Then only the numbers with larger numbers will be enumerated later If you put it in the back group , It must still be in the first position ( If there is a number with a smaller number and this number form a legal scheme , The previous enumeration will be ) But this number has no solution in the first position , So this whole branch has no solution It's the case of the last stick Mainly using the hypothetical method , Then equivalent replacement , Push out contradictions */
// Coming here means that this stick is not good
int j=i;// and i A stick of the same length is definitely not good
while(j<n&&w[j]==w[i]) j++;
i=j-1;
}
return false;
}
int main(){
while(cin>>n,n){
memset(st,0,sizeof st);
str=len=sum=0;
for(int i=0;i<n;i++){
cin>>w[i];
sum+=w[i];
}
sort(w,w+n,greater<int>());// Enumerate from the maximum length , Fewer states are enumerated
str=w[0];// Start with the maximum length
while(1){
// Enumerate from small to large str, Once found break, You must get the smallest
if(sum%str==0&&dfs(0,0,0)) break;// Must satisfy str yes len The divisor of can be divided into several groups
str++;
}
cout<<str<<endl;
}
return 0;
}
Birthday cake
Topic link : Birthday cake
analysis : A very abnormal question . Be careful : The answer to the question is not monotonous , Therefore, we cannot divide .
Feeling AcWing The explanation of a user's question is very good , I won't make a fool of myself . Answer link : Birthday cake
Code implementation :
#include<iostream>
#include<cmath>
using namespace std;
const int N=25,INF=1e9;
int minv[N],mins[N];//minv[i] Before presentation i The minimum volume required for the layer
int n,m;
int res=INF;
int R[N],H[N];// Record the radius and height of each layer
void dfs(int u,int s,int v){
//u Is the current number of layers ,s Is the used area ,v Is the used volume
if(s+mins[u]>=res) return ;
if(v+minv[u]>n) return ;
if(s+2*(n-v)/R[u+1]>=res) return ;
if(!u){
if(v==n) res=s;
return ;
}
// Search order , First R after H, From big to small
for(int r=min(R[u+1]-1,(int)sqrt((n-v-minv[u-1])/u));r>=u;r--)
for(int h=min(H[u+1]-1,(n-v-minv[u-1])/r/r);h>=u;h--){
H[u]=h,R[u]=r;
if(u==m) dfs(u-1,s+2*r*h+r*r,v+r*r*h);
else dfs(u-1,s+2*r*h,v+r*r*h);
// There is no need to restore the scene , Because you can't use these later H[u],R[u] 了 , When they are used again, they are also modified first and then used
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
minv[i]=minv[i-1]+i*i*i;
mins[i]=mins[i-1]+2*i*i;
}
R[m+1]=H[m+1]=INF;// Reduce boundary judgment
dfs(m,0,0);// Search from the lowest level
if(INF==res) res=0;
cout<<res<<endl;
return 0;
}
Iteration deepening
What does iteration deepening mean ? In us dfs In the process , There will be multiple branches , Maybe we can find the answer from a branch in a very shallow layer , The other branch is as deep as a bottomless hole , In fact, we can't roughly judge the depth of the search layer, and the depth may vary a lot , At this time, we can artificially design a layer , Starting from the limitation that you can only search one layer , Gradually relax restrictions , Until you find the answer or no solution , Generally speaking, the number of states in the previous layers is less than that in the last layer , Therefore, we will not spend much more time , So we can do this in case we find a very bad path, but the answer is in another short path . This method is also often related to what we will talk about next IDA* The combination of algorithms .
Addition sequence
Topic link : Addition sequence
analysis : Just follow the above idea to write code , In fact, it is very different from kuansou .
Code implementation :
#include<iostream>
using namespace std;
const int N=110;
int path[N],n;
bool dfs(int u,int depth){
if(u==depth) return path[u-1]==n;// If you finish searching the last floor , Judge whether the result is correct and return
bool st[N]={
0};
for(int i=u-1;i>=0;i--)// Enumeration from large to small , Fewer cases
for(int j=i;j>=0;j--){
int s=path[i]+path[j];
if(s>n||s<=path[u-1]||st[s]) continue;// If s Greater than n perhaps s Less than or equal to the last number or s Already enumerated ( For example, there is 1,2,3, that 3 Will be enumerated 2 Time ), Just continue
st[s]=1;
path[u]=s;// Add the sequence
if(dfs(u+1,depth)) return true;
// There is no need to restore the scene , because path[u] Will be covered
}
return false;
}
int main(){
path[0]=1;// The first number is 1
while(cin>>n,n){
int depth=1;
while(!dfs(1,depth)) depth++;
for(int i=0;i<depth;i++) cout<<path[i]<<" ";
puts("");
}
return 0;
}
two-way DFS
It feels like a two-way DFS That's strange , May be y I always get up by myself ? Let's look at it through a question .
giving gifts
Topic link : giving gifts
analysis : well ! This is not 01 Backpack ? Take a look at the volume , Excuse me . We found that the number of items is relatively small , Therefore, we can consider explosive search , Direct search seems to explode , So we consider metaphysics Optimize , We can divide all items into two groups , In the first group, we directly use explosion search to find that the weight of all energy components is less than or equal to W Weight of , Then enumerate each number of the second group and add it to each combination , This will optimize a lot , Of course , You can also find out how many of the two groups of items are optimal , As for the enumeration weight , We must enumerate from large to small , See code for details .
Code implementation :
Say two-way BFS It's really like two-way , This DFS?
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long LL;
int w,n,k;
const int N=50;
int ans;
//cnt from 1 Start , because weight[0]=0 It's also a plan , That is, don't move anything
int a[N],weight[1<<25],cnt=1;//weight Record all the weight found ,cnt Record quantity , Because the first group has at most 23 Number , Therefore, the maximum weight is 2 Of 23 Inferior species
void dfs1(int u,int s){
//s Record the current and
if(u==k){
weight[cnt++]=s;
return ;
}
dfs1(u+1,s);// Not this number
if((LL)s+a[u]<=w) dfs1(u+1,s+a[u]);// Choose this number
}
void dfs2(int u,int s){
if(u>=n){
// If all the numbers are considered , Find less than or equal to w Maximum number of , And update the answer (if possible)
int l=0,r=cnt-1;
while(l<r){
int mid=l+r+1>>1;
if((LL)s+weight[mid]<=w) l=mid;
else r=mid-1;
}
ans=max(ans,s+weight[l]);
return ;
}
dfs2(u+1,s);// Not this number
if((LL)s+a[u]<=w) dfs2(u+1,s+a[u]);// Choose this number
}
int main(){
cin>>w>>n;
for(int i=0;i<n;i++) cin>>a[i];
sort(a,a+n,greater<int>());
k=n/2;//k Represents the number of the first group
dfs1(0,0);// Find out all the weights of the first group ( Less than or equal to W Of ), Consider altogether 0~k-1 this k Number
sort(weight,weight+cnt);
cnt=unique(weight,weight+cnt)-weight;// Sort and de duplicate , use cnt Record the array size after de duplication
dfs2(k,0);// From k Start thinking about each number
cout<<ans<<endl;
return 0;
}
IDA*
you 're right , It's the metaphysical algorithm again , I feel this is A* Brother of Algorithm , It is often used with iteration deepening , The most difficult thing is to find the method of estimating the distance .
Arrange books
Topic link : Arrange books
analysis : This problem will have very different operation steps according to different situations , So we consider iteration deepening , And there are too many situations in this problem , We can enumerate the length of the operation , You can also enumerate the insertion locations , sure TLE, We think about optimization . We found that , After arranging the order , The successor of each number ( That is, the number after it ) Are equal to this number +1, And one of our moves , At most, it will only change the successor of three numbers ( It is recommended to operate manually ), Therefore, we can count the number that does not meet the correct subsequent number , Divide this number by 3 The number obtained by rounding up is regarded as the minimum number of steps , Then we judge whether the sum of the minimum steps and the current steps is greater than the maximum steps , If it is larger than, cut this branch directly , It feels like a strategy A* Algorithm , But it's more like a pruning strategy . Sure enough, the most difficult thing to search is pruning .
Code implementation :
#include<iostream>
#include<cstring>
using namespace std;
const int N=15;
int T,q[N],w[5][N],n;//w Array storage q Backup of , Because it may be multi-layered at the same time , Therefore, it should be opened in two dimensions
int g(){
// Return the estimated number of steps from the current state to the end
int cnt=0;
for(int i=0;i<n-1;i++)
if(q[i]+1!=q[i+1])
cnt++;
return (cnt+2)/3;// return cnt Divide 3 The value rounded up , It's better not to write (cnt-1)/3+1, Because even if cnt by 0 And will return to 1, I've been writing like this before, but I didn't miss it , I know I met this problem .
}
bool check(){
// Check whether the current status is legal
for(int i=0;i<n-1;i++)
if(q[i]+1!=q[i+1])
return false;
return true;
}
bool dfs(int u,int d){
if(u+g()>d) return false;
if(check()) return true;
for(int len=1;len<=n;len++)
for(int l=0;l+len-1<n;l++){
int r=l+len-1;
// Because inserting this group of numbers to the front is equivalent to inserting a group of numbers to the back , This situation has been enumerated
for(int k=r+1;k<n;k++){
// Enumerate where to insert , Just push it back
memcpy(w[u],q,sizeof q);// Under backup , Restore the scene with
int x,y;
// The insert
for(x=r+1,y=l;x<=k;x++,y++)q[y]=w[u][x];
for(x=l;x<=r;x++,y++) q[y]=w[u][x];
if(dfs(u+1,d)) return true;
memcpy(q,w[u],sizeof q);// Restore scene
}
}
return false;
}
int main(){
cin>>T;
while(T--){
cin>>n;
for(int i=0;i<n;i++) cin>>q[i];
int d=0;
while(d<5&&!dfs(0,d)) d++;// It is possible that it is correct not to search the first floor , So from the first 0 The first floor starts searching
if(d>=5) puts("5 or more");
else cout<<d<<endl;
}
return 0;
}
Swing Game
Topic link : Swing Game
analysis : For this question , How can we find the shortest operand ? We found that , middle 8 The largest number corresponds to the least operation steps , Suppose the most is cnt individual , Then our shortest operand is 8-cnt 了 , Because an operation will send out a number and bring in a number , The best case is to enter a number different from the maximum number , Come in with the same number . But the inscription is really cumbersome , We can make a table to simplify the operation , We use a two-dimensional array to store each operation , Make the corresponding operations of each operation the same , In this way, our code is greatly simplified .
Code implementation :
#include<iostream>
using namespace std;
// It's really a kind of technique to type a watch !
const int op[8][7]={
// Record the numerical coordinates corresponding to each operation , Make each operation become the number exchange corresponding to two adjacent coordinates ( The first and the last are also considered adjacent )
{
0,2,6,11,15,20,22},
{
1,3,8,12,17,21,23},
{
10,9,8,7,6,5,4},
{
19,18,17,16,15,14,13},
{
23,21,17,12,8,3,1},
{
22,20,15,11,6,2,0},
{
13,14,15,16,17,18,19},
{
4,5,6,7,8,9,10}
};
const int opposite[8]={
5,4,7,6,1,0,3,2};// Record the reverse operation of each operation , If we did it last time A, Don't enumerate this time F 了 , Because then execute F It's equivalent to going back
const int center[8]={
6,7,8,11,12,15,16,17};// Record the numerical coordinates of the eight grids of the target
const int N=24;
int q[N],path[100];//path What is stored is the operation method , use 0~7 Express , When output, it is converted to A~H
int g(){
// Valuation function
int sum[4]={
0};
for(int i=0;i<8;i++) sum[q[center[i]]]++;
int m=0;
for(int i=1;i<4;i++) m=max(m,sum[i]);
return 8-m;
}
void operate(int x){
int t=q[op[x][0]];
for(int i=0;i<6;i++) q[op[x][i]]=q[op[x][i+1]];
q[op[x][6]]=t;
}
bool dfs(int u,int d,int last){
// We record last, That is, the operation of the previous step
if(u+g()>d) return false;
if(!g()) return true;
for(int i=0;i<8;i++){
if(opposite[i]==last) continue;
operate(i);
path[u]=i;
if(dfs(u+1,d,i)) return true;
operate(opposite[i]);// Restore the scene
}
return false;
}
int main(){
while(cin>>q[0],q[0]){
for(int i=1;i<24;i++) cin>>q[i];
int d=0;
while(!dfs(0,d,-1)) d++;
if(!d) cout<<"No moves needed";
else
for(int i=0;i<d;i++)
cout<<char('A'+path[i]);// Note that the force turns to char, Otherwise, the number will be printed
cout<<endl<<q[6]<<endl;// The first 6 The three positions correspond to 8 One of
}
return 0;
}
The search is finally over , In fact, we have already talked about the search content , Basically, there is only one dance chain left , But this thing is more difficult , Put it in the back and talk about it alone .
边栏推荐
- How much do you know about the bank deposit business that software test engineers must know?
- 如何解决ecology9.0执行导入流程流程产生的问题
- 【DesignMode】适配器模式(adapter pattern)
- MySQL之函数
- 云呐|固定资产管理系统功能包括哪些?
- Yunna | what are the main operating processes of the fixed assets management system
- 上门预约服务类的App功能详解
- 选择致敬持续奋斗背后的精神——对话威尔价值观【第四期】
- 【DesignMode】组合模式(composite mode)
- 微信小程序---WXML 模板语法(附带笔记文档)
猜你喜欢
Ffmpeg learning - core module

Miaochai Weekly - 8

Upgrade openssl-1.1.1p for openssl-1.0.2k
教你在HbuilderX上使用模拟器运行uni-app,良心教学!!!

Key structure of ffmpeg -- AVCodecContext
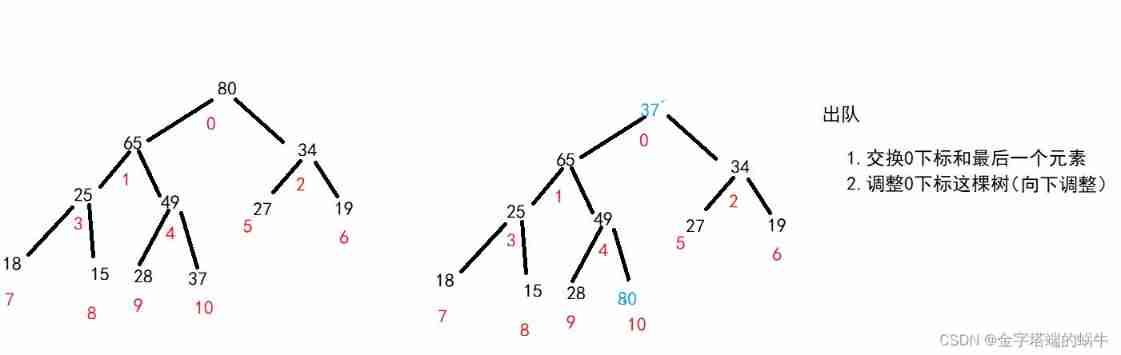
Priority queue (heap)
Detailed explanation of APP functions of door-to-door appointment service
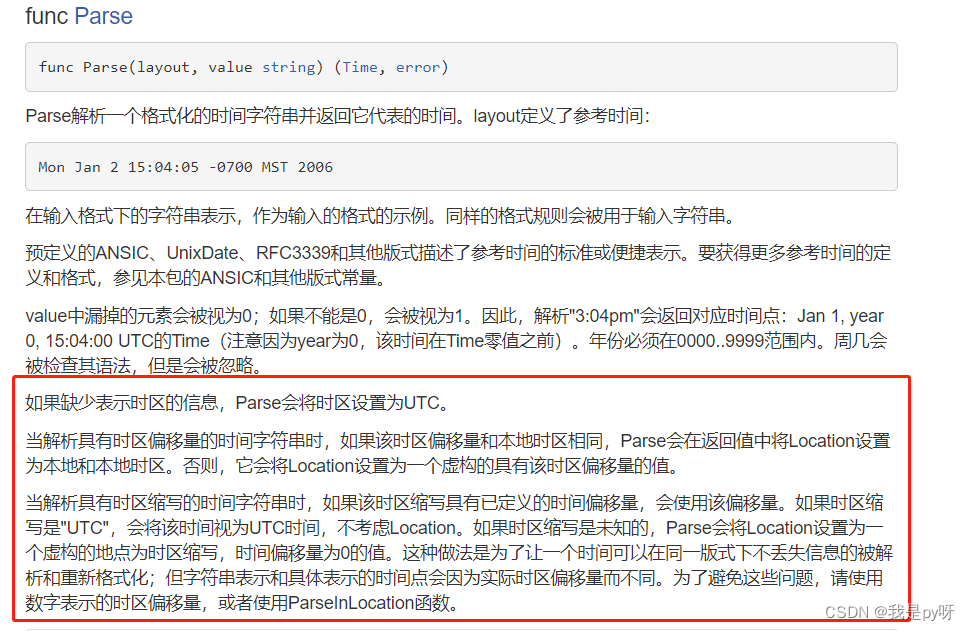
时区的区别及go语言的time库
About the slmgr command
QT QPushButton details
随机推荐
【luogu CF487E】Tourists(圆方树)(树链剖分)(线段树)
云呐|固定资产管理系统功能包括哪些?
从底层结构开始学习FPGA----FIFO IP核及其关键参数介绍
Permission problem: source bash_ profile permission denied
[online chat] the original wechat applet can also reply to Facebook homepage messages!
Hudi of data Lake (1): introduction to Hudi
wx. Getlocation (object object) application method, latest version
CloudCompare&PCL 点云随机添加噪声
USB Interface USB protocol
Global and Chinese markets for pressure and temperature sensors 2022-2028: Research Report on technology, participants, trends, market size and share
Initialiser votre vecteur & initialisateur avec une liste Introduction à la Liste
What is information security? What is included? What is the difference with network security?
Miaochai Weekly - 8
FFmpeg学习——核心模块
Zhuan: in the future, such an organization can withstand the risks
Senparc. Weixin. Sample. MP source code analysis
Key structure of ffmpeg - avformatcontext
MySQL global lock and table lock
Redis high availability - master-slave replication, sentinel mode, cluster
提升工作效率工具:SQL批量生成工具思想