当前位置:网站首页>【二叉搜索树】增删改查功能代码实现
【二叉搜索树】增删改查功能代码实现
2022-07-05 23:35:00 【UkeLiu】
二叉树的基本结构就不介绍了,这里主要给大家上干货,用代码实现二叉树的排序规则,遍历和插入,删除功能。
排序规则
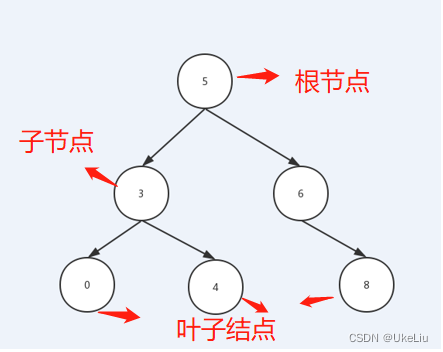
二叉搜索树又叫二叉查找树、二叉排序树具备一下几个特点:
- 如果它的左子树不为空,则左子树上结点的值都小于根结点。
- 如果它的右子树不为空,则右子树上结点的值都大于根结点。
- 子树同样也要遵循以上两点
二叉树的遍历
首先我们用链表的形式实现一个二叉树:
//定义树的节点
class treeNode{
private int data; //数据
private treeNode left; //左节点
private treeNode right; //右节点
private treeNode parent;//父节点
public treeNode getParent() {
return parent;
}
public void setParent(treeNode parent) {
this.parent = parent;
}
public treeNode(int data, treeNode left, treeNode right) {
this.data = data;
this.left = left;
this.right = right;
}
public treeNode(int data){
this.data = data;
this.left = null;
this.right = null;
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public treeNode getLeft() {
return left;
}
public void setLeft(treeNode left) {
this.left = left;
}
public treeNode getRight() {
return right;
}
public void setRight(treeNode right) {
this.right = right;
}
}
//输出节点数据的方法
public void print(treeNode treeNode){
System.out.println(treeNode.getData());
}
public static void main(String[] args) {
//测试一下数据
treeNode H=new treeNode('H',null,null);
treeNode K=new treeNode('k',null,null);
treeNode G=new treeNode('G',H,K);
treeNode F=new treeNode('F',G,null);
treeNode E=new treeNode('E',null,F);
treeNode D=new treeNode('D',null,null);
treeNode C=new treeNode('C',D,null);
treeNode B=new treeNode('B',null,C);
treeNode A=new treeNode('A',B,E);
BinaryTree binaryTree = new BinaryTree();
System.out.println("前---->");
binaryTree.pre(A);
System.out.println();
System.out.println("中---->");
binaryTree.in(A);
System.out.println();
System.out.println("后---->");
binaryTree.post(A);
System.out.println();
}
这里实现的是一个如下图所示的一个二叉树: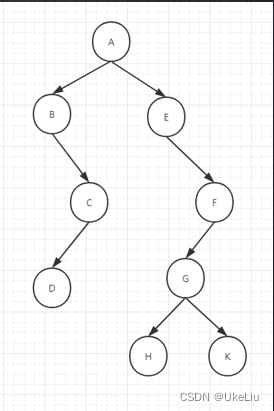
二叉树有三种遍历方式:
- 前序遍历 :根左右(从二叉树的根节点开始遍历,依次输出),可以这样理解先看根节点,有直接输出,第二个看左节点,有左节点输出,再看左节点有没有子树,有的话重复上面的操作,右节点也一样,这里面设计到递归回溯的一个算法思想。
- 中序遍历:左根右
- 后序遍历:左右根
这三种遍历方式其实就是从上往下,从下往上,还有一层一层的三种遍历方式,而口诀就是根左右,左根右,左右根。
代码实现:
/** * 前序遍历 根左右 */
public void pre(treeNode treeNode){
print(treeNode);//输出根节点数据
if (treeNode.getLeft()!=null){
//左节点不为空
pre(treeNode.getLeft()); //递归再看根左右
}
if (treeNode.getRight()!=null){
//同上原理
pre(treeNode.getRight());
}
}
/** * 中序遍历 左根右 */
public void in(treeNode treeNode){
if (treeNode.getLeft()!=null){
in(treeNode.getLeft());
}
print(treeNode);
if (treeNode.getRight()!=null){
in(treeNode.getRight());
}
}
/** * 中序遍历 左右根 */
public void post(treeNode treeNode){
if (treeNode.getLeft()!=null){
post(treeNode.getLeft());
}
if (treeNode.getRight()!=null){
post(treeNode.getRight());
}
print(treeNode);
}
二叉树的插入:二叉树的插入就非常的简单的,因为他的特性,我们插入一个数,从根节点开始,只要比根节点小就往左边走,比根节点大就往右边走,在跟下一个节点比较,直到比较的节点没有子节点为止。
代码:
/** * 二叉搜索树插入数据 * @param root 根节点 * @param data 插入的值 */
public void insert(treeNode root,int data){
//每次插入的时候都要跟根节点进行比较
if (data<root.getData()){
//如果比根节点小就往左边走
if (root.getLeft()==null){
//如果是叶子结点 直接将结点加在叶子结点左边
treeNode treeNode = new treeNode(data, null, null);
treeNode.setParent(root); //设置新插入节点的父节点
root.setLeft(treeNode);
}else {
insert(root.getLeft(),data);
}
}else {
if (root.getRight()==null){
treeNode treeNode = new treeNode(data, null, null);
treeNode.setParent(root);;
root.setRight(treeNode);
}else {
insert(root.getRight(),data);
}
}
}
二叉树的删除
二叉树的删除是最难的,但是他难得并不是删除操作,而是指针的指向问题,二叉树的删除分为三种情况:
要删除的节点是叶子结点,这样的话,直接删除就好了,因为他没有复杂的指向问题,时间复杂度是O(1)
删除的节点有左或者右子树,这种情况也很简单只需要将他的子节点指向他的父节点就好了,时间复杂度也是O(1)
删除的节点有左右子树,这个时候我们就要去查找他的后继节点或者是前继节点,后继节点就是他的右子树中最小的数,前继节点就是左子树中最大的数。
我们以后继节点为例,用后继节点代替删除节点的位置,这个时候后继节点也是相当于删除了,我们还要去考虑后继节点是否存在右子树,后继节点是肯定的不存在左子树的,因为后继节点是删除节点右子树最小的数,这样我们就会往左边走,直到找到最左边的数就是后继节点。
代码比较复杂,我注释的也比较仔细,大家如果有不懂的地方可以留言,看到会给大家解答
class treeNode{
private int data; //数据
private treeNode left; //左节点
private treeNode right; //右节点
private treeNode parent;//父节点
public treeNode getParent() {
return parent;
}
public void setParent(treeNode parent) {
this.parent = parent;
}
public treeNode(int data, treeNode left, treeNode right) {
this.data = data;
this.left = left;
this.right = right;
}
public treeNode(int data){
this.data = data;
this.left = null;
this.right = null;
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public treeNode getLeft() {
return left;
}
public void setLeft(treeNode left) {
this.left = left;
}
public treeNode getRight() {
return right;
}
public void setRight(treeNode right) {
this.right = right;
}
}
/** * 使用链表实现二叉树 */
public class BinaryTree {
public static void main(String[] args) {
BinaryTree binaryTree = new BinaryTree();
treeNode root = null;
Scanner cin = new Scanner(System.in);
int t = 1;
System.out.println("二叉搜索树假定不存重复的子节点,重复可用链表处理,请注意~~");
System.out.println("请输入根节点:");
int rootData = cin.nextInt();
root = new treeNode(rootData);
System.out.println("请输入第" + t + "个点:输入-1表示结束");
while (true) {
//
int data = cin.nextInt();
if (data == -1)
break;
binaryTree.insert(root, data);
t++;
System.out.println("请输入第" + t + "个点:输入-1表示结束");
}
binaryTree.show(root); //找的别人写的打印二叉树形结构,感觉还不错,可以更加清晰
System.out.println("删除测试:");
while(true) {
System.out.println("请输入要删除的点:-1表示结束");
int key = cin.nextInt();
root = binaryTree.delNode(key,root);
binaryTree.show(root);
if(root == null) {
System.out.println("树已经没有数据了~~");
break;
}
}
}
public void print(treeNode treeNode){
System.out.println(treeNode.getData());
}
// 用于获得树的层数
public int getTreeDepth(treeNode root) {
return root == null ? 0 : (1 + Math.max(getTreeDepth(root.getLeft()), getTreeDepth(root.getRight())));
}
private void writeArray(treeNode currNode, int rowIndex, int columnIndex, String[][] res, int treeDepth) {
// 保证输入的树不为空
if (currNode == null)
return;
// 先将当前节点保存到二维数组中
res[rowIndex][columnIndex] = String.valueOf(currNode.getData());
// 计算当前位于树的第几层
int currLevel = ((rowIndex + 1) / 2);
// 若到了最后一层,则返回
if (currLevel == treeDepth)
return;
// 计算当前行到下一行,每个元素之间的间隔(下一行的列索引与当前元素的列索引之间的间隔)
int gap = treeDepth - currLevel - 1;
// 对左儿子进行判断,若有左儿子,则记录相应的"/"与左儿子的值
if (currNode.getLeft() != null) {
res[rowIndex + 1][columnIndex - gap] = "/";
writeArray(currNode.getLeft(), rowIndex + 2, columnIndex - gap * 2, res, treeDepth);
}
// 对右儿子进行判断,若有右儿子,则记录相应的"\"与右儿子的值
if (currNode.getRight() != null) {
res[rowIndex + 1][columnIndex + gap] = "\\";
writeArray(currNode.getRight(), rowIndex + 2, columnIndex + gap * 2, res, treeDepth);
}
}
/** * 展示二叉树 * @param root */
public void show(treeNode root) {
if (root == null) {
System.out.println("EMPTY!");
return ;
}
// 得到树的深度
int treeDepth = getTreeDepth(root);
// 最后一行的宽度为2的(n - 1)次方乘3,再加1
// 作为整个二维数组的宽度
int arrayHeight = treeDepth * 2 - 1;
int arrayWidth = (2 << (treeDepth - 2)) * 3 + 1;
// 用一个字符串数组来存储每个位置应显示的元素
String[][] res = new String[arrayHeight][arrayWidth];
// 对数组进行初始化,默认为一个空格
for (int i = 0; i < arrayHeight; i++) {
for (int j = 0; j < arrayWidth; j++) {
res[i][j] = " ";
}
}
// 从根节点开始,递归处理整个树
writeArray(root, 0, arrayWidth / 2, res, treeDepth);
// 此时,已经将所有需要显示的元素储存到了二维数组中,将其拼接并打印即可
for (String[] line : res) {
StringBuilder sb = new StringBuilder();
for (int i = 0; i < line.length; i++) {
sb.append(line[i]);
if (line[i].length() > 1 && i <= line.length - 1) {
i += line[i].length() > 4 ? 2 : line[i].length() - 1;
}
}
System.out.println(sb.toString());
}
}
/** * 二叉搜索树插入数据 * @param root 根节点 * @param data 插入的值 */
public void insert(treeNode root,int data){
//每次插入的时候都要跟根节点进行比较
if (data<root.getData()){
//如果比根节点小就往左边走
if (root.getLeft()==null){
//如果是叶子结点 直接将结点加在叶子结点左边
treeNode treeNode = new treeNode(data, null, null);
treeNode.setParent(root); //设置新插入节点的父节点
root.setLeft(treeNode);
}else {
insert(root.getLeft(),data);
}
}else {
if (root.getRight()==null){
treeNode treeNode = new treeNode(data, null, null);
treeNode.setParent(root);;
root.setRight(treeNode);
}else {
insert(root.getRight(),data);
}
}
}
/** * 二叉树删除结点数据 * @param data */
public treeNode delNode(int data,treeNode root){
//找到这个节点。遍历这个树
treeNode delNode = selectNode(data, root);
//节点未找到
if (delNode==null){
System.out.println("删除节点不存在树中");
}
if (root==delNode){
return null;
}
//如果这个节点是叶子结点 就直接删除
if (delNode.getRight()==null && delNode.getLeft()==null){
treeNode parent = delNode.getParent();
//判断节点是在那一边
if (delNode.getData()< parent.getData()){
//在左边
parent.setLeft(null);
}else {
parent.setRight(null);
}
}else if (delNode.getRight()!=null && delNode.getLeft()!=null){
//删除的节点 有两个子节点
//查找后继节点
treeNode successorNode = selectSuccessorNode(delNode);
successorNode.setLeft(delNode.getLeft()); //将删除点的左子树指向后继节点的左边
successorNode.getLeft().setParent(successorNode); //将左子树的父节点指向后继节点
//后继节点的左节点肯定是空的,我们需要判断一下后继节点的右节点是否有值
if (successorNode.getRight()==null){
//如果后继节点没有右节点 直接将后继节点删除
if(delNode!=successorNode.getParent()){
//将后继节点的右边子树指向删除节点的右边子树
successorNode.setRight(delNode.getRight());
//将删除节点右边父节点指向后继节点
delNode.getRight().setParent(successorNode);
//删除后继节点
successorNode.getParent().setLeft(null);
}
}else if (successorNode.getRight()!=null && delNode!=successorNode.getParent()){
//将后继节点的右边子树指向删除节点的右边子树
successorNode.setRight(delNode.getRight());
//将删除节点右边父节点指向后继节点
delNode.getRight().setParent(successorNode);
//将后继节点的右子树的父节点指向后继节点的父节点左子树
successorNode.getRight().setParent(successorNode.getParent());
//将后继节点的父节点左子树指向后继节点的右子树
successorNode.getParent().setLeft(successorNode.getRight());
}
//指针替换完成 下一步就是删除节点
if (delNode==root){
successorNode.setParent(null);
root=successorNode;
return root;
}
successorNode.setParent(delNode.getParent());
//判断一下删除的点是在父节点的左边还是右边
if (delNode.getParent().getData()>delNode.getData()){
//在左边
delNode.getParent().setLeft(successorNode);
}else {
delNode.getParent().setRight(successorNode);
}
}else{
//删除节点只有一个子节点
if (delNode.getRight()!=null){
//只有右边节点
if (delNode==root){
root=delNode.getRight();
return root;
}
delNode.getRight().setParent(delNode.getParent());
//判断一下删除的点是在父节点的左边还是右边
if (delNode.getParent().getData()>delNode.getData()){
//在左边
delNode.getParent().setLeft(delNode.getRight());
}else {
delNode.getParent().setRight(delNode.getRight());
}
}else {
//只有左边结点
if (delNode==root){
root=delNode.getLeft();
return root;
}
delNode.getLeft().setParent(delNode.getParent());
//判断一下删除的点是在父节点的左边还是右边
if (delNode.getParent().getData()>delNode.getData()){
//在左边
delNode.getParent().setLeft(delNode.getLeft());
}else {
delNode.getParent().setRight(delNode.getLeft());
}
}
}
return root;
}
/** * 二叉树删除有两种方式 一个是查找前继节点:查找节点左侧比节点值最大的数 * 查找节点的后继节点:查找右侧节点比节点值最小的数 * 这个方法实现的查找后继节点 前继节点代码一样 查找方向换一下就是了 * @param node * @return */
public treeNode selectSuccessorNode(treeNode node){
//找节点右边所有节点比节点小的数
if (node.getRight()==null){
//说明没有后继节点
return node;
}
treeNode cur=node.getRight();
treeNode pre=node.getRight(); //开一个额外的空间存储node 因为当node左节点为空时,返回的是上一个节点
while (cur!=null){
pre=cur;
cur=cur.getLeft();
}
return pre;
}
/** *查找需要删除的节点 * @data 节点数据 * @root 根节点 * @return 删除的节点 */
public treeNode selectNode(int data,treeNode root){
treeNode current=root;
while (current != null){
if (current.getData()<data){
current=current.getRight();
}else if (current.getData()>data){
current=current.getLeft();
}else {
return current;
}
}
return null;
}
}
边栏推荐
- 14 MySQL view
- Part III Verilog enterprise real topic of "Niuke brush Verilog"
- 激光slam学习记录
- Rasa 3. X learning series -rasa 3.2.1 new release
- Open3D 点云随机添加噪声
- 同事悄悄告诉我,飞书通知还能这样玩
- poj 2762 Going from u to v or from v to u? (infer whether it is a weak link diagram)
- White hat talks about web security after reading 2
- ts类型声明declare
- Tips for using pads router
猜你喜欢
保研笔记二 软件工程与计算卷二(13-16章)
Scala concurrent programming (II) akka
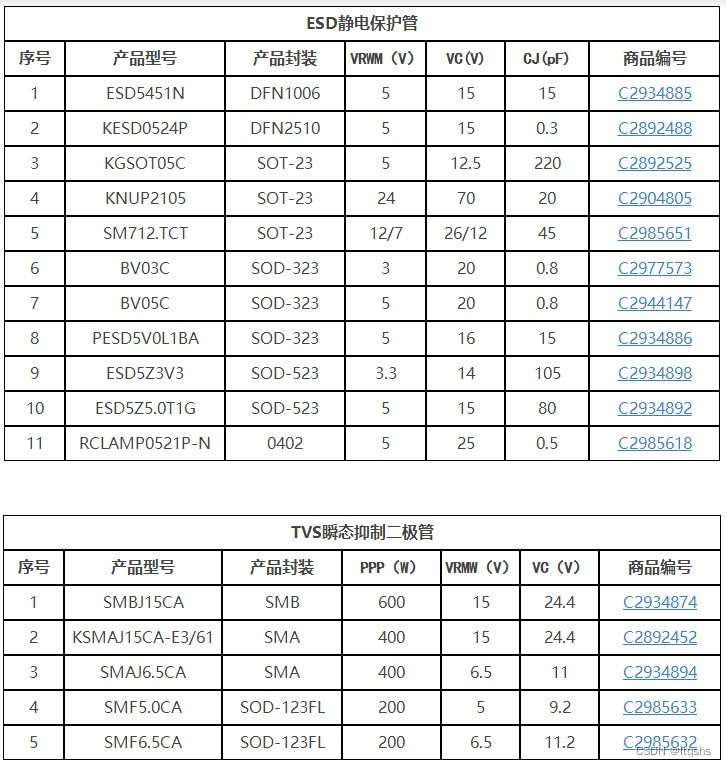
TVS管和ESD管的技术指标和选型指南-嘉立创推荐

CIS基准测试工具kube-bench使用

Neural structured learning - Part 2: training with natural graphs
Attacking technology Er - Automation
Open source CRM customer relationship system management system source code, free sharing

开源crm客户关系统管理系统源码,免费分享
SpreadJS 15.1 CN 与 SpreadJS 15.1 EN

Rasa 3. X learning series -rasa x Community Edition (Free Edition) changes
随机推荐
Convert Chinese into pinyin
Rasa 3.x 学习系列-Rasa X 社区版(免费版) 更改
Qcombox (rewrite) + qcompleter (auto completion, auto loading the drop-down options of qcombox, setting the background color)
Senparc.Weixin.Sample.MP源码剖析
Spire Office 7.5.4 for NET
Common static methods of math class
Naoqi robot summary 26
C # input how many cards are there in each of the four colors.
15 MySQL stored procedures and functions
LeetCode——Add Binary
18.(arcgis api for js篇)arcgis api for js点采集(SketchViewModel)
Technical specifications and model selection guidelines for TVs tubes and ESD tubes - recommended by jialichuang
Make a short video clip number of we media film and television. Where can I download the material?
开源crm客户关系统管理系统源码,免费分享
White hat talks about web security after reading 2
5. Logistic regression
[Yu Yue education] NC machining technology reference materials of Shaanxi University of science and technology
2022.6.20-6.26 AI industry weekly (issue 103): new little life
芯源&立创EDA训练营——无刷电机驱动
Rasa 3. X learning series -rasa x Community Edition (Free Edition) changes