当前位置:网站首页>Mathematical model Lotka Volterra
Mathematical model Lotka Volterra
2022-07-05 23:51:00 【jeff one】
mathematical model Lotka-Volterra
origin :
20 century 40 years ,Lotka(1925) and Volterra(1926) Laid a theoretical foundation for interspecific competition , The interspecific competition equation proposed by them has a significant impact on the development of modern ecological theory .
Content :
Lotka-Volterra Model (Lotka-Volterra Interspecific competition model ) yes logistic Model ( Growth retardation model ) Extension of . Now set the following parameters :
N1、N2: Are the population numbers of the two species
K1、K2: The environmental capacity of the two species
r1、r2 : Are the population growth rates of the two species
According to the logistic model, there are the following relationships :
among :N/K It can be understood as the space that has been used ( be called “ Space item used ”), be (1-N/K) It can be understood as unused space ( be called “ Unused space items ”)
When two species compete or use the same space ,“ Space item used ” You should also add N2 The occupation of space by the population . be :

among ,α: species 2 For species 1 Competition coefficient , each N2 The space occupied by individuals is equivalent to α individual N1 Space occupied by individuals .
Then there are ,β: species 1 For species 2 Competition coefficient , each N1 The space occupied by individuals is equivalent to β individual N2 Space occupied by individuals . There is another :

As we know :
When species N1 population ( species 1) The environmental capacity of is K1 when ,N1 The inhibitory effect of each individual in the population on the growth of its own population is 1/K1; Empathy ,N2 The inhibitory effect of each individual in the population on the growth of its own population is 1/K2.
in addition , from (1)、(2) Two equations and α、β From the definition of :
N2 Each individual in the population pairs N1 The effect of population is :α/K1
N1 Each individual in the population pairs N2 The effect of population is :β/K2
therefore , When species 2 Can inhibit species 1 when , It can be said that , species 2 For species 1 Influence > species 2 The impact on oneself , namely α/K1 > 1/K2.
边栏推荐
- 多普勒效应(多普勒频移)
- 哪些偏门项目可以做到?自媒体做到月赚一万以上很难吗?
- Qcombox (rewrite) + qcompleter (auto completion, auto loading the drop-down options of qcombox, setting the background color)
- How to insert data into MySQL database- How can I insert data into a MySQL database?
- 15 MySQL-存储过程与函数
- Redis高可用——主从复制、哨兵模式、集群
- Rasa 3.x 学习系列-Rasa 3.2.1 新版本发布
- QCombox(重写)+QCompleter(自动补全,自动加载qcombox的下拉选项,设置背景颜色)
- Latex multiple linebreaks
- Zhongjun group launched electronic contracts to accelerate the digital development of real estate enterprises
猜你喜欢

保研笔记一 软件工程与计算卷二(1-7章)
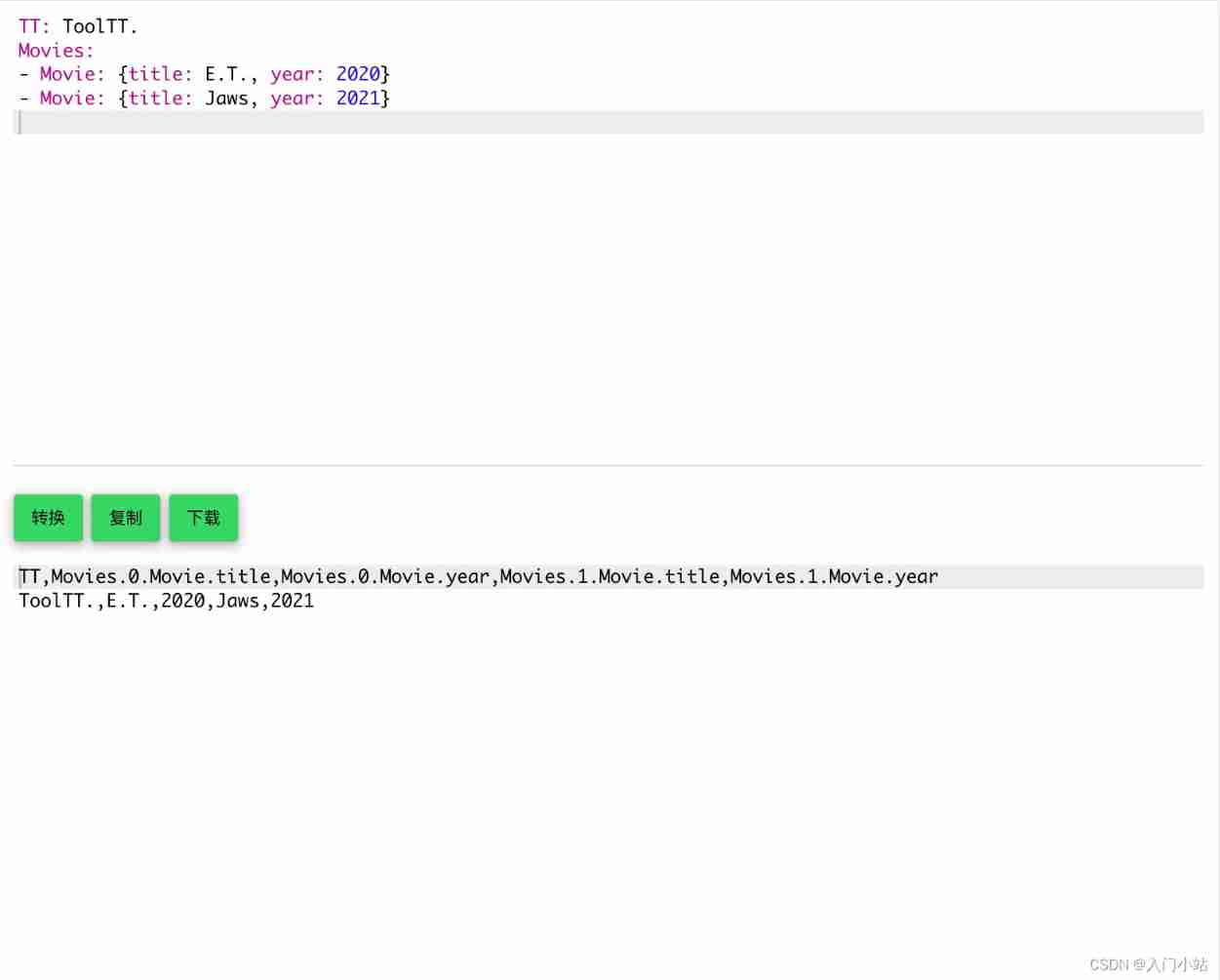
Online yaml to CSV tool
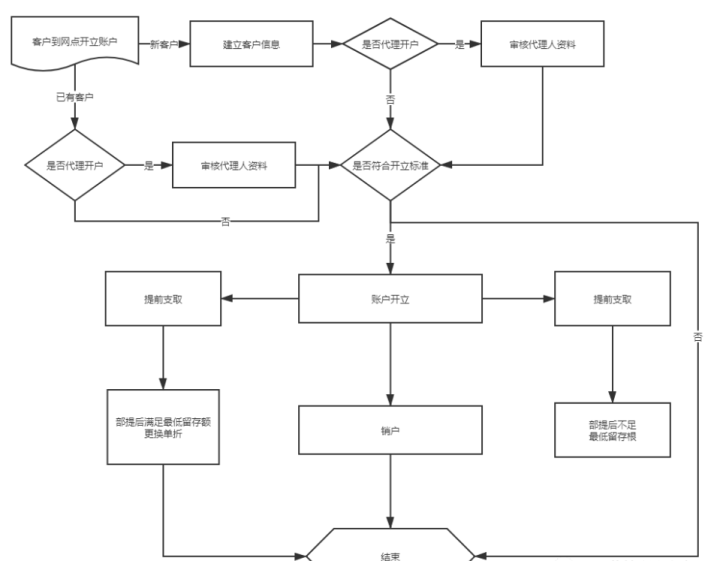
软件测试工程师必会的银行存款业务,你了解多少?
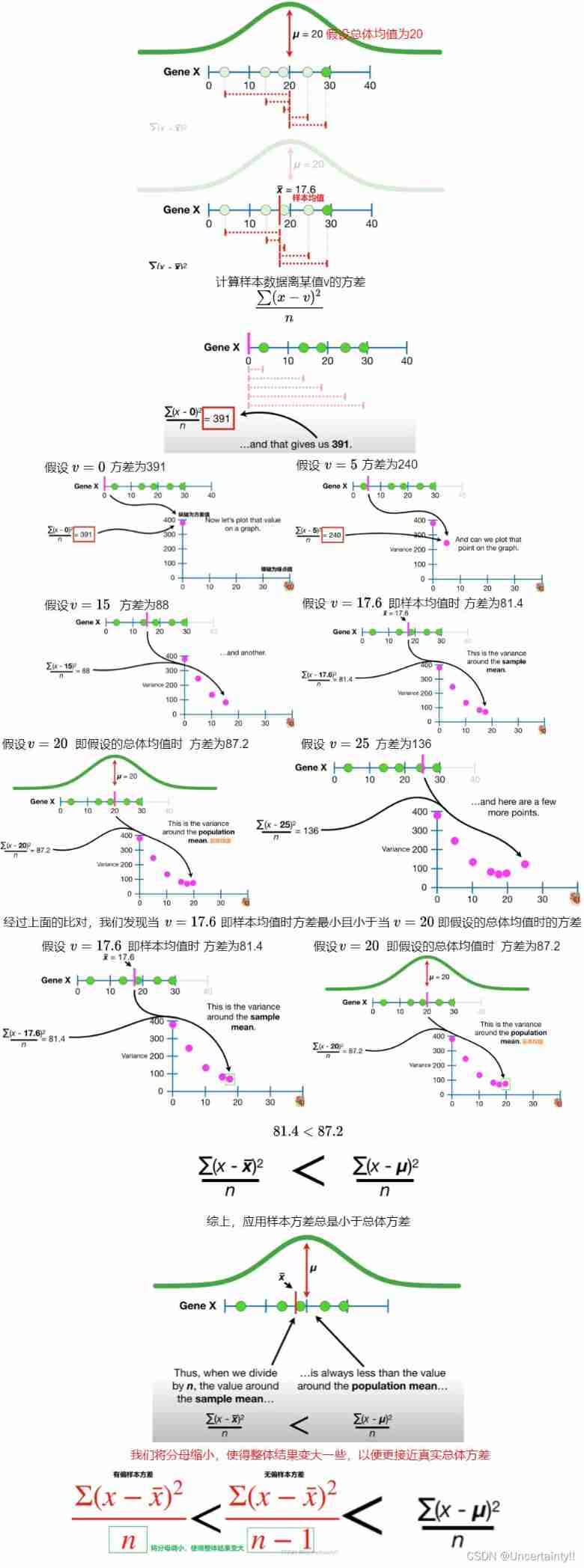
Biased sample variance, unbiased sample variance
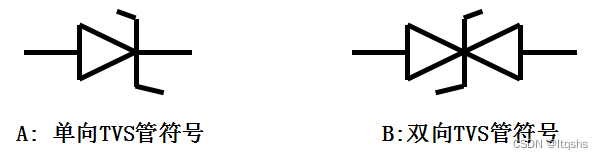
Comparison of parameters between TVs tube and zener diode

传输层协议------UDP协议
98. Verify the binary search tree ●●

总结了 800多个 Kubectl 别名,再也不怕记不住命令了!

Rasa 3.x 学习系列-Rasa X 社区版(免费版) 更改
亲测可用fiddler手机抓包配置代理后没有网络
随机推荐
MySQL delete uniqueness constraint unique
When to use useImperativeHandle, useLayoutEffect, and useDebugValue
11gR2 Database Services for " Policy" and " Administrator" Managed databases (file I
Part III Verilog enterprise real topic of "Niuke brush Verilog"
Initialize your vector & initializer with a list_ List introduction
有什么不起眼却挣钱的副业?
帶外和帶內的區別
STM32__06—单通道ADC
教你在HbuilderX上使用模拟器运行uni-app,良心教学!!!
How to rotate the synchronized / refreshed icon (EL icon refresh)
20220703 周赛:知道秘密的人数-动规(题解)
QT--线程
Switching power supply buck circuit CCM and DCM working mode
Biased sample variance, unbiased sample variance
【luogu CF487E】Tourists(圆方树)(树链剖分)(线段树)
MySQL replace primary key delete primary key add primary key
Open3D 点云随机添加噪声
GFS分布式文件系統
哪些偏门项目可以做到?自媒体做到月赚一万以上很难吗?
Laser slam learning record