当前位置:网站首页>[Luogu cf487e] tours (square tree) (tree chain dissection) (line segment tree)
[Luogu cf487e] tours (square tree) (tree chain dissection) (line segment tree)
2022-07-05 23:49:00 【SSL_ TJH】
Tourists
Topic link :luogu CF487E
The main idea of the topic
Here's an undirected graph , Then a little bit of power .
Then you may modify the point weight at a single point every time , Or ask the point with the least weight in all paths between two points .
Ideas
It's not difficult to think of a round square tree when you see all these paths .
Then we consider that the square point is the minimum value of the origin to which it is connected .
Then you will find that if there is any modification, you will get stuck every time O ( n ) O(n) O(n)( Meganium )
Then consider a wonderful way , Is to consider the special place of this figure , It's a tree .
The reason why you get stuck is that you have to update everything , That update must be updated , The question is whether we can update only a part first , Then when you ask, get the missing part .
If the structure of the tree, can we only get our son , Then every time I update, I only update my father .
Then you think about the part of tree chain dissection , That's except LCA Is it OK for Fang Dian to get his father to do anything else .
Then the rest is simple , Just ordinary round square tree , Ordinary tree chain segmentation plus segment tree maintenance minimum .
Code
#include<set>
#include<cstdio>
#include<vector>
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1e5 + 100;
int n, m, q, w[N << 1], tot;
vector <int> G[N], GG[N << 1];
multiset <int> sum[N];
struct SLPF {
int dfn[N << 1], son[N << 1], sz[N << 1], fa[N << 1], top[N << 1], a[N << 3], deg[N << 1], dy[N << 1];
void dfs1(int now, int father) {
sz[now] = 1; fa[now] = father; deg[now] = deg[father] + 1;
for (int i = 0; i < GG[now].size(); i++) {
int x = GG[now][i]; if (x == father) continue;
dfs1(x, now); sz[now] += sz[x]; if (sz[x] > sz[son[now]]) son[now] = x;
}
if (now > n) {
for (int i = 0; i < GG[now].size(); i++) {
int x = GG[now][i]; if (x == father) continue;
sum[now - n].insert(w[x]);
}
w[now] = *sum[now - n].begin();
}
}
void dfs2(int now, int father) {
dfn[now] = ++dfn[0]; dy[dfn[0]] = now;
if (son[now]) {
top[son[now]] = top[now]; dfs2(son[now], now);
}
for (int i = 0; i < GG[now].size(); i++) {
int x = GG[now][i]; if (x == father || x == son[now]) continue;
top[x] = x; dfs2(x, now);
}
}
void up(int now) {
a[now] = min(a[now << 1], a[now << 1 | 1]);
}
void build(int now, int l, int r) {
if (l == r) {
a[now] = w[dy[l]]; return ;
}
int mid = (l + r) >> 1;
build(now << 1, l, mid); build(now << 1 | 1, mid + 1, r);
up(now);
}
void change(int now, int l, int r, int pl) {
if (l == r) {
a[now] = w[dy[pl]]; return ;
}
int mid = (l + r) >> 1;
if (pl <= mid) change(now << 1, l, mid, pl); else change(now << 1 | 1, mid + 1, r, pl);
up(now);
}
int query(int now, int l, int r, int L, int R) {
if (L <= l && r <= R) {
return a[now];
}
int mid = (l + r) >> 1, re = 2e9;
if (L <= mid) re = min(re, query(now << 1, l, mid, L, R));
if (mid < R) re = min(re, query(now << 1 | 1, mid + 1, r, L, R));
return re;
}
int ask(int x, int y) {
int re = 2e9;
while (top[x] != top[y]) {
if (deg[top[x]] < deg[top[y]]) swap(x, y);
re = min(re, query(1, 1, tot, dfn[top[x]], dfn[x]));
x = fa[top[x]];
}
if (deg[x] > deg[y]) swap(x, y);
re = min(re, query(1, 1, tot, dfn[x], dfn[y]));
if (x > n) re = min(re, w[fa[x]]);
return re;
}
}T;
struct YF_tree {
int dfn[N], low[N], sta[N];
void link(int x, int y) {
GG[x].push_back(y); GG[y].push_back(x);}
void tarjan(int now) {
dfn[now] = low[now] = ++dfn[0]; sta[++sta[0]] = now;
for (int i = 0; i < G[now].size(); i++) {
int x = G[now][i];
if (!dfn[x]) {
tarjan(x); low[now] = min(low[now], low[x]);
if (dfn[now] == low[x]) {
tot++;
while (sta[sta[0]] != x) {
link(sta[sta[0]], tot); sta[0]--;
}
link(sta[sta[0]], tot); sta[0]--;
link(now, tot);
}
}
else low[now] = min(low[now], dfn[x]);
}
}
void Init() {
tot = n;
for (int i = 1; i <= n; i++) if (!dfn[i]) tarjan(i);
T.dfs1(1, 0); T.dfs2(1, 0);
}
}H;
int main() {
scanf("%d %d %d", &n, &m, &q);
for (int i = 1; i <= n; i++)
scanf("%d", &w[i]);
for (int i = 1; i <= m; i++) {
int x, y; scanf("%d %d", &x, &y);
G[x].push_back(y); G[y].push_back(x);
}
H.Init();
T.build(1, 1, tot);
while (q--) {
char c = getchar(); while (c != 'C' && c != 'A') c = getchar();
if (c == 'A') {
int x, y; scanf("%d %d", &x, &y);
printf("%d\n", T.ask(x, y));
}
else {
int x, y; scanf("%d %d", &x, &y);
if (T.fa[x]) {
sum[T.fa[x] - n].erase(w[x]); sum[T.fa[x] - n].insert(y);
w[T.fa[x]] = *sum[T.fa[x] - n].begin(); T.change(1, 1, tot, T.dfn[T.fa[x]]);
}
w[x] = y; T.change(1, 1, tot, T.dfn[x]);
}
}
return 0;
}
边栏推荐
- Spire Office 7.5.4 for NET
- Neural structured learning - Part 3: training with synthesized graphs
- Rasa 3. X learning series -rasa 3.2.1 new release
- Introduction to JVM
- 21. PWM application programming
- GFS Distributed File System
- SpreadJS 15.1 CN 与 SpreadJS 15.1 EN
- How to get all the values stored in localstorage
- 21.PWM应用编程
- 如何提升口才
猜你喜欢
Fiddler Everywhere 3.2.1 Crack

保研笔记一 软件工程与计算卷二(1-7章)
Rasa 3. X learning series -rasa 3.2.1 new release
【LeetCode】5. Valid Palindrome·有效回文
Spreadjs 15.1 CN and spreadjs 15.1 en
同事悄悄告诉我,飞书通知还能这样玩

Spire.PDF for NET 8.7.2
MySQL delete uniqueness constraint unique

Redis高可用——主从复制、哨兵模式、集群
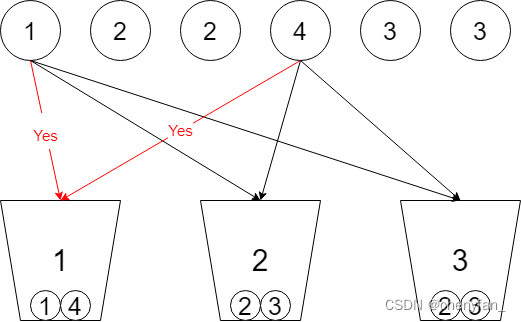
698. Divided into k equal subsets ●●
随机推荐
Make a short video clip number of we media film and television. Where can I download the material?
Qt QPushButton详解
Zero rhino technology joined hands with the intelligence Club: the "causal faction" forum was successfully held, and the "causal revolution" brought the next generation of trusted AI
el-cascader的使用以及报错解决
Introduction to JVM
Rethinking about MySQL query optimization
Research notes I software engineering and calculation volume II (Chapter 1-7)
STM32__ 06 - single channel ADC
GFS Distributed File System
C# 文件与文件夹操作
When to use useImperativeHandle, useLayoutEffect, and useDebugValue
JVM details
5. Logistic regression
Do you regret becoming a programmer?
Objective C message dispatch mechanism
【SQL】各主流数据库sql拓展语言(T-SQL 、 PL/SQL、PL/PGSQL)
Rsync remote synchronization
【GYM 102832H】【模板】Combination Lock(二分图博弈)
Neural structured learning - Part 2: training with natural graphs
Fiddler Everywhere 3.2.1 Crack