当前位置:网站首页>AtCoder Beginner Contest 258【比赛记录】
AtCoder Beginner Contest 258【比赛记录】
2022-07-06 00:06:00 【瘾ิۣۖิۣۖิۣۖิꦿ】
比赛过程非常不顺,D题INF开小了,wrong了好几发,还要边输入边操作时忘记处理不合理的情况了,心态崩溃,最后喜提掉分!!!
ABC
模拟即可,注意B不要都错题,不要拐弯!!!C不要数组越界,自己RE了几发!!!
D Trophy
贪心,枚举要玩的前缀1~i个,最后全部给第i个,找到最小值即可。
#include <bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define rep2(i,a,b) for(int i=a;i>=b;i--)
#define sc(x) scanf("%d",&x)
#define sl(x) scanf("%lld",&x)
#define ll long long
const int Max=5e5+5;
int main(){
ll n,x;
cin>>n>>x;
ll mina=0;ll ans=0;
ll a,b;
cin>>a>>b;
ans+=(a+b);
mina=ans+(x-1)*b;
for(ll i=1;i<n;i++){
cin>>a>>b;
ans+=(a+b);
if(x>i){
ll temp=ans+(x-i-1)*b;
mina=min(mina,temp);
}
}
cout<<mina<<endl;
}E Packing Potatoes
预处理每个下标作为起点时能到达的终点。发现查询的K最大为1e12,故不可循环访问,这时候就需要用到倍增,加快查询速度。
#include <bits/stdc++.h>
using namespace std;
#define sc(x) scanf("%d",&x)
#define sl(x) scanf("%lld",&x)
#define ll long long
#define pb push_back
const int Max=2e5+5;
ll w[Max];
ll sum[Max];
int n,q,x;
int ne[45][Max];
ll res[Max];
ll getsum(ll l,ll r){
ll ans=0;
bool flag=false;
if((l-1)/n!=(r-1)/n) ans=((r-1)/n-(l-1)/n-1)*(sum[n]);
else flag=true;
if(l%n==0) l=n;
else l%=n;
if(r%n==0) r=n;
else r%=n;
if(flag) return sum[r]-sum[l-1];
return ans+sum[n]-sum[l-1]+sum[r];
}
void solve(int p){
ll l=p,r=p+1000000000,_l=l;
while(l<=r){
ll mid=(l+r)/2;
if(getsum(_l,mid)>=1ll*x) r=mid-1;
else l=mid+1;
}
res[p]=l-p+1;
ne[0][p]=l+1;
while(ne[0][p]>n) ne[0][p]-=n;
}
int main(){
sc(n);sc(q);sc(x);
for(int i=1;i<=n;i++){
sl(w[i]);sum[i]=sum[i-1]+w[i];
}
for(int i=1;i<=n;i++) solve(i);
for(int j=1;j<=40;j++){
for(int i=1;i<=n;i++){
ne[j][i]=ne[j-1][ne[j-1][i]];
}
}
while(q--){
ll k;sl(k);k--;
ll ans=1;
for(int i=40;~i;i--){
if(k-(1ll<<i)>=0){
// cout<<ans<<' ';
ans=ne[i][ans];k-=(1ll<<i);
// cout<<ans<<' '<<k<<endl;
}
}
// cout<<ans<<' ';
cout<<res[ans]<<endl;
}
}F Main Street
F过的人少,因为这题特判特别多,一不小心就少判,或者判错。这里附上大佬的代码!!!
#include <iostream>
#include <string>
#include <cstring>
#include <cstdio>
#include <set>
#include <map>
#include <cmath>
#include <queue>
#include <algorithm>
#include <array>
using namespace std;
#define forn(i, n) for(int i = 0; i < (int)(n); i++)
#define ford(i, n) for (int i = (int)(n) - 1; i >= 0; --i)
#define forab(i, a, b) for(int i=(a);i<(b);++i)
#define foreach(i, n) for (__typeof(n.begin()) i = n.begin(); i != n.end(); ++i)
#define sqr(x) ((x)*(x))
#define clr(a, b) memset(a, b, sizeof(a))
#define MP make_pair
#define PB push_back
#define SZ(a) ((int)a.size())
#define all(a) (a).begin(),(a).end()
#define inf 0x3f3f3f3f
typedef long long ll;
typedef vector<int> vi;
typedef vector<ll> vll;
typedef pair<int, int> pii;
const double eps = 1e-8;
int dcmp(double x) { if (x < -eps) return -1; else return x > eps;}
#define se(x) cout<<#x<<" = "<<x<<endl
#ifdef CHEN_PC
#define debug(...) printf(__VA_ARGS__)
#else
#define debug(...)
#endif
const int N = 200010;
const int mod = 1000000007; // 10^9+7
int n;
int solve() {
ll b, k, sx, sy, gx, gy;
cin >> b >> k >> sx >> sy >> gx >> gy;
ll ans = (abs(sx - gx) + abs(sy - gy)) * k;
forn (i, 4) forn (j, 4) {
ll cur = 0;
auto gao = [&] (ll x, ll y, int dir) {
if (dir == 0) {
cur += (x % b) * k;
x = x / b * b;
}
if (dir == 1) {
cur += (b - x % b) * k;
x = x / b * b + b;
}
if (dir == 2) {
cur += (y % b) * k;
y = y / b * b;
}
if (dir == 3) {
cur += (b - y % b) * k;
y = y / b * b + b;
}
return MP(x, y);
};
auto [ux, uy] = gao(sx, sy, i);
auto [vx, vy] = gao(gx, gy, j);
cur += abs(ux - vx) + abs(uy - vy);
if (ux != vx && uy / b == vy / b) {
ll d = min(min(uy-uy/b*b, vy-vy/b*b), min(uy/b*b+b-uy, vy/b*b+b-vy));
cur += d * 2;
}
if (uy != vy && ux / b == vx / b) {
ll d = min(min(ux-ux/b*b, vx-vx/b*b), min(ux/b*b+b-ux, vx/b*b+b-vx));
cur += d * 2;
}
ans = min(ans, cur);
}
cout << ans << endl;
return 0;
}
int main(int argc, char *argv[]) {
#ifdef CHEN_PC
freopen("in.txt", "r", stdin);
#endif
while (cin >> n) {
forn (i, n)
int ret = solve();
// cout << ret << endl;
}
return 0;
}
G Triangle
枚举 1≤i<j≤n 且 ai,j=1, 考虑有多少个 k 满足 ai,k=aj,k=1 都有边。发现这个东西就是 |Si∩Sj|,其中 Si表示满足 j>i,ai,j=1 的 j 的集合,于是可以用 bitset处理。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int Max=3050;
bitset<Max>mp[Max];
char a[Max][Max];
int main(){
int n;cin>>n;
for(int i=0;i<n;i++){
scanf("%s",a[i]);
mp[i]=bitset<Max>(a[i]);
}
ll ans=0;
for(int i=0;i<n;i++){
for(int j=0;j<i;j++){
if(a[i][j]=='1'){
ans+=(mp[i]&mp[j]).count();
}
}
}
cout<<ans/3<<endl;
}Ex Odd Steps
这里可以将题目比作“上台阶,一个人从第一个台阶,每一步只能迈出奇数步,最终到达S的可能性,其中下标为A的台阶不可落脚。”,这时我们假设dp[i]为到达台阶i时的可能性,那么
dp[i]=dp[i-1]+dp[i-3]+dp[i-5]...再假设s[i]为:
s[i]=dp[i]+dp[i-2]+dp[i-4]...故:
dp[i]=dp[i-1]+s[i-3]这时我们发现S=1e18,循环查询完全不可能,可以用矩阵表示:
![\begin{bmatrix} dp[i-1] & s[i-2] &s[i-3] \\ 0& 0& 0\\ 0& 0 & 0 \end{bmatrix}](http://img.inotgo.com/imagesLocal/202207/06/202207060006405149_1.gif) *
*  =
= ![\begin{bmatrix} dp[i] & s[i-1] &s[i-2] \\ 0 &0 &0 \\ 0& 0& 0 \end{bmatrix}](http://img.inotgo.com/imagesLocal/202207/06/202207060006405149_0.gif)
因为出现在A数组的下标dp[i]=0,故中间快速幂求解的同时记得将某些值赋值为0.
#include <bits/stdc++.h>
using namespace std;
#define sc(x) scanf("%d",&x)
#define sl(x) scanf("%lld",&x)
#define ll long long
#define pb push_back
const int Max=2e5+5;
const int Mod=998244353;
struct Matrix{
ll a[3][3];
friend Matrix operator *(const Matrix &a,const Matrix &b){
Matrix ans;
for(int i=0;i<3;i++){
for(int j=0;j<3;j++){
ll sum=0;
for(int k=0;k<3;k++){
sum+=a.a[i][k]*b.a[k][j];
sum%=Mod;
}
ans.a[i][j]=sum;
}
}
return ans;
}
}trans;
Matrix quick_power(Matrix a,ll b){
Matrix ans;
for(int i=0;i<3;i++){
for(int j=0;j<3;j++){
ans.a[i][j]=0;
}
}
ans.a[0][0]=ans.a[1][1]=ans.a[2][2]=1;
while(b){
if(b&1){
ans=ans*a;
}
b>>=1;
a=a*a;
}
return ans;
}
ll a[Max];
ll b[Max];
int main(){
int n;ll S;
sc(n);sl(S);
trans.a[0][0]=1;
trans.a[1][0]=0;
trans.a[2][0]=1;
trans.a[0][1]=1;
trans.a[1][1]=0;
trans.a[2][1]=1;
trans.a[0][2]=0;
trans.a[1][2]=1;
trans.a[2][2]=0;
Matrix ans;
for(int i=0;i<3;i++){
for(int j=0;j<3;j++){
ans.a[i][j]=0;
}
}
ans.a[0][0]=1;
ll sum=0;
for(int i=1;i<=n;i++){
sl(a[i]);
ans=ans*quick_power(trans,a[i]-a[i-1]);
ans.a[0][0]=0;
}
ans=ans*quick_power(trans,S-a[n]);
cout<<ans.a[0][0]<<endl;
}边栏推荐
- 多普勒效應(多普勒頻移)
- Hardware and interface learning summary
- 行列式学习笔记(一)
- Configuring OSPF load sharing for Huawei devices
- Initialize your vector & initializer with a list_ List introduction
- FFmpeg学习——核心模块
- [QT] QT uses qjson to generate JSON files and save them
- Online yaml to CSV tool
- 云呐|固定资产管理系统功能包括哪些?
- Wechat applet -- wxml template syntax (with notes)
猜你喜欢
C reflection and type
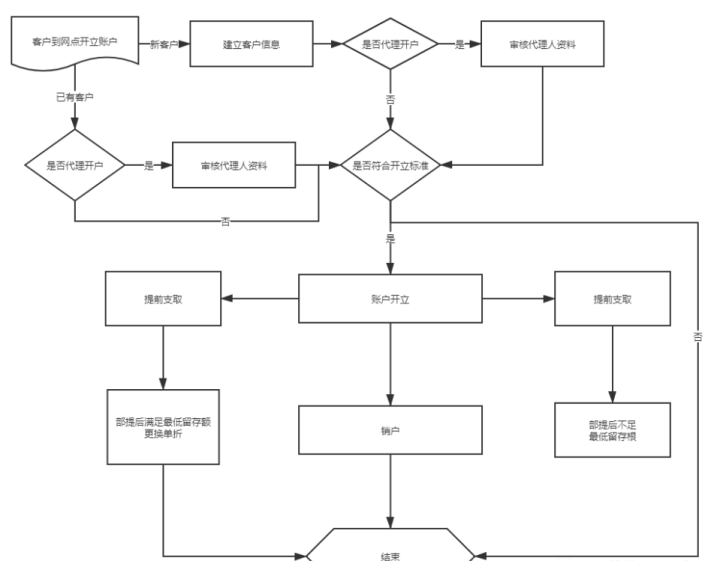
软件测试工程师必会的银行存款业务,你了解多少?
Hudi of data Lake (1): introduction to Hudi
![[day39 literature extensive reading] a Bayesian perspective on magnetic estimation](/img/9c/438ef820a9f703c21f708bfc1dbbc4.jpg)
[day39 literature extensive reading] a Bayesian perspective on magnetic estimation
![[binary search tree] add, delete, modify and query function code implementation](/img/38/810a83575c56f17a7a0ed428a2e02e.png)
[binary search tree] add, delete, modify and query function code implementation
MySql——CRUD
Hudi of data Lake (2): Hudi compilation

云呐|固定资产管理系统主要操作流程有哪些

18. (ArcGIS API for JS) ArcGIS API for JS point collection (sketchviewmodel)
Tools to improve work efficiency: the idea of SQL batch generation tools
随机推荐
Huawei equipment is configured with OSPF and BFD linkage
Zhuan: in the future, such an organization can withstand the risks
【EF Core】EF Core与C# 数据类型映射关系
QT a simple word document editor
【QT】Qt使用QJson生成json文件并保存
Mathematical model Lotka Volterra
Online yaml to CSV tool
VBA fast switching sheet
用列錶初始化你的vector&&initializer_list簡介
【luogu P3295】萌萌哒(并查集)(倍增)
mysql-全局锁和表锁
Permission problem: source bash_ profile permission denied
认识提取与显示梅尔谱图的小实验(观察不同y_axis和x_axis的区别)
Hudi of data Lake (1): introduction to Hudi
wx. Getlocation (object object) application method, latest version
QT QPushButton details
MySQL之函数
"14th five year plan": emphasis on the promotion of electronic contracts, electronic signatures and other applications
[designmode] composite mode
7.5 decorator