Determinant learning notes (I)

What is determinant

The textbook defines the second-order determinant like this .
For a system of binary linear equations ：

\[\begin{cases} a_{11}x + a_{12}y = b_1\\ a_{21}x + a_{22}y = b_2 \end{cases} \]

After elimination, you can get ：

\[(a_{12}a_{21}-a_{22}a_{11})y=a_{21}b_1-a_{11}b_2 \]

\(x\) The same principle can be obtained .
We found that when \(a_{12}a_{21} \neq a_{22}a_{11}\) The equation has a unique solution .
At this time, let's say \(a_{11}a_{22}-a_{12}a_{21}\)：

\[\begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22}\\ \end{vmatrix} = a_{11}a_{22}-a_{12}a_{21}\]

So I didn't understand the use at all .

---

Now let's introduce a better understanding method .
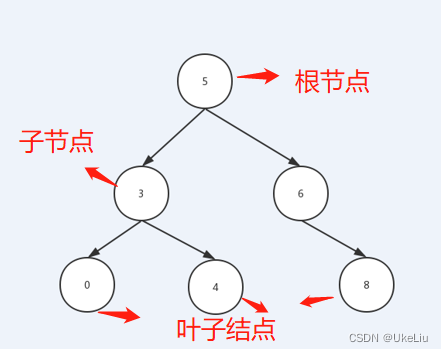
We know “ A matrix can represent a set of vectors , Matrix representation \(n\) individual \(n\) Dimension vector ”.
That is, each line is treated as a vector , Combine all vectors vertically to determine one \(n\) Dimensional graphics .
Take a look at a two-dimensional picture ：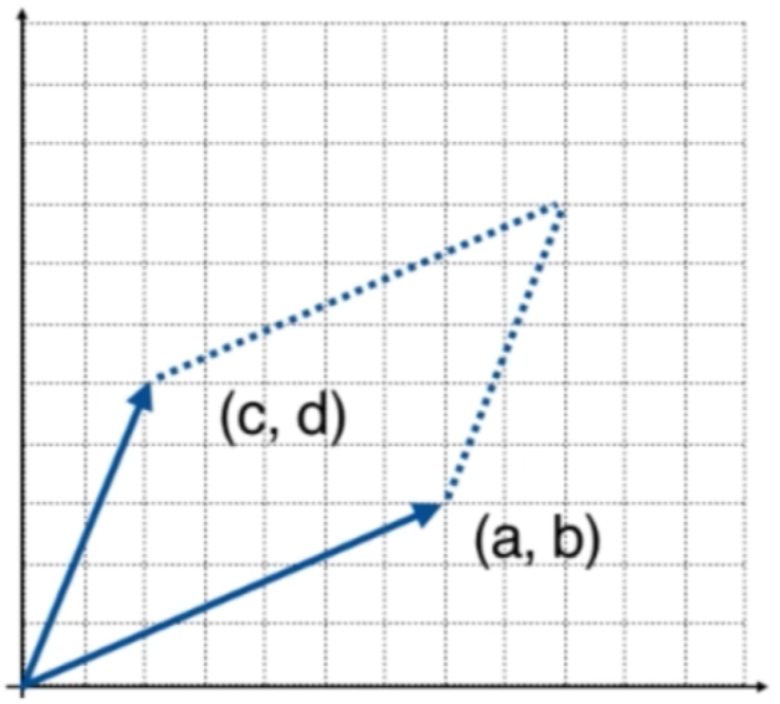

Our second-order determinant is shown in the figure above The area of a parallelogram .
Of course , Two dimensions are areas , Three dimensional is volume , The fourth dimension is ？？？ ……
The area of the parallelogram above can be expressed as ：

\[\det A = \begin{vmatrix} a & b\\ c & d\\ \end{vmatrix} \]

be aware , Each row corresponds to a vector in the above figure .

Finding determinant

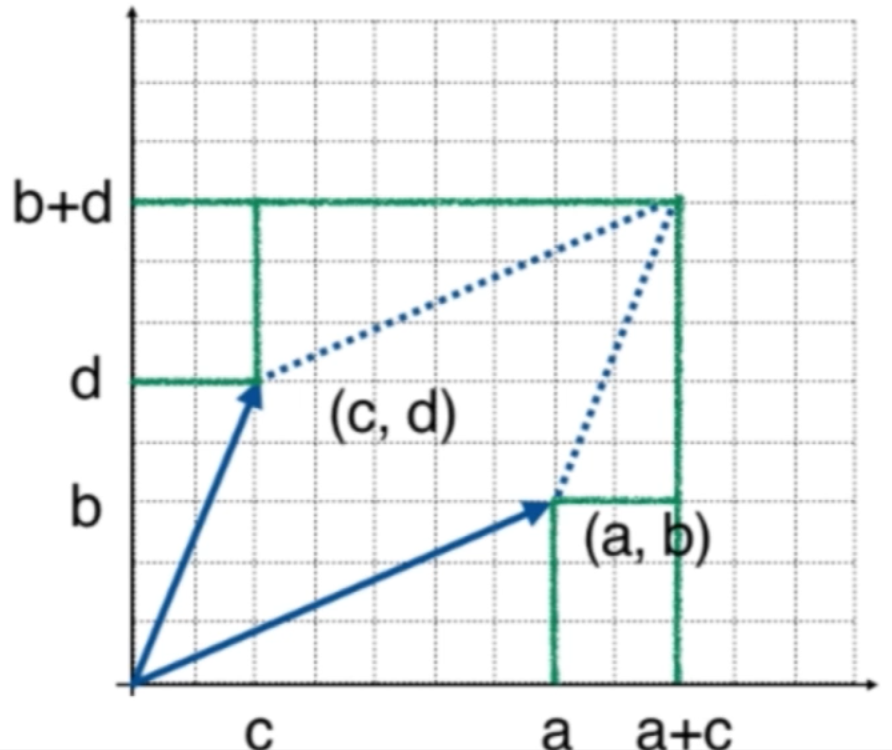
We start with primary school mathematics , First find the area of the parallelogram （ The auxiliary line practice is omitted ）

\[\begin{split} S_{ parallelogram } &=(a+c)(b+d)-2bc-cd-ab \\ &=ad-bc\\ &=\det A \end{split}\\ \]

That is to say ：

\[\begin {vmatrix} a &b \\ c &d \\ \end {vmatrix} = ad-bc \]

The basic properties of determinants

Let's discuss it with the second-order determinant .

Property one

\[\det I = 1 \]

\(I\) Represents the unit matrix , That makes sense ：
All vectors are “ Horizontal and vertical ” And the length is one , The area must be \(1\).

Property two

Exchange the two lines of a determinant , Then the value of the determinant is reversed .
Expressed by mathematical formula ：

\[\begin{vmatrix} a & b\\ c & d\\ \end{vmatrix}= -\begin{vmatrix} c &d\\ a & b\\ \end{vmatrix} \]

The proof is simple ：

\[\begin{vmatrix} a & b\\ c & d\\ \end{vmatrix} = ad-bc\\ \]

\[\begin{split} \begin{vmatrix} c &d\\ a & b\\ \end{vmatrix}&=bc-ad\\ &=-(ad-bc)\\ &=-\begin{vmatrix} c &d\\ a & b\\ \end{vmatrix} \end{split} \]

Property three

Express it directly with mathematical formulas .（ Chinese is not good ）

\[\begin{vmatrix} ka & kb\\ c &d\\ \end{vmatrix} =k \begin{vmatrix} a & b\\ c &d\\ \end{vmatrix} \]

Simply prove it .

\[\begin{split} \begin{vmatrix} ka & kb\\ c &d\\ \end{vmatrix} &= kad-kbc\\&=k(ad-bc) \end{split} \]

Be careful ：\(\det (kA) \neq k\det (A)\)
For the second-order determinant ：

\[\begin{split} \det (kA) &= \begin {vmatrix} ka &kb\\ kc & kd\\ \end {vmatrix}\\ &=ka\times kd - kc \times kb\\ &=k^2(ad-bc)\\ &=k^2 \begin{vmatrix} a &b\\ c & d\\ \end {vmatrix}=k ^2\det (A) \end {split} \]

From this we can deduce , about \(n\) Determinant of order ：

\[\det (kA)=k^n\det (A) \]

Property 4

One row of the matrix plus one row , Then there are ：

\[\begin{vmatrix} a+a' & b + b'\\ c & d\\ \end{vmatrix} =\begin{vmatrix} a & b\\ c & d\\ \end{vmatrix} + \begin{vmatrix} a' & b'\\ c & d\\ \end{vmatrix} \]

prove ：

\[\begin{split} \begin{vmatrix} a+a' & b + b'\\ c & d\\ \end{vmatrix} &=(a+a')d-c(b+b')\\ &=ad+a'd-cb-cb'\\ &=(ad-bc)+(a'd-b'c)\\ &= \begin{vmatrix} a & b\\ c & d\\ \end{vmatrix} + \begin{vmatrix} a' & b'\\ c & d\\ \end{vmatrix} \end{split} \]