当前位置:网站首页>Convert binary search tree into cumulative tree (reverse middle order traversal)
Convert binary search tree into cumulative tree (reverse middle order traversal)
2022-07-06 00:51:00 【Hydrion-Qlz】
538. Convert binary search tree to accumulation tree
difficulty : secondary
Give a binary Search for Root node of tree , The node values of the tree are different , Please convert it to an accumulation tree (Greater Sum Tree), Make each node node The new value of is equal to or greater than in the original tree node.val The sum of the values of .
As a reminder , The binary search tree satisfies the following constraints :
- The left subtree of a node contains only the key Less than Node key node .
- The right subtree of a node contains only the key Greater than Node key node .
- Left and right subtrees must also be binary search trees .
** Be careful :** This topic and 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ identical
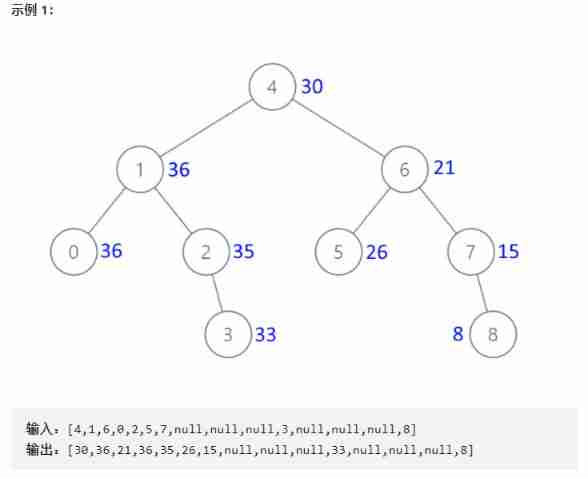
Ideas
I began to see that this problem was also a little confused , Thought of using middle order traversal , But it has never been possible to calculate , Took a look at the official solution , Referred to the Reverse middle order traversal , Well, I fixed my mind
If it is a positive mid order traversal , Then we traverse the elements from small to large
If it is reverse middle order traversal , Then our traversal order is from big to small
At this time, set a variable to count the current sum , When traversing an element , Add its value to sum in , And then sum Copy to node.val, Then go through the next element
package cn.edu.xjtu.carlWay.tree.BST2GreaterTree;
import cn.edu.xjtu.Util.TreeNode.TreeNode;
/** * 538. Convert binary search tree to accumulation tree * Give a binary Search for Root node of tree , The node values of the tree are different , Please convert it to an accumulation tree (Greater Sum Tree), Make each node node The new value of is equal to or greater than in the original tree node.val The sum of the values of . * <p> * As a reminder , The binary search tree satisfies the following constraints : * <p> * The left subtree of a node contains only the key Less than Node key node . * The right subtree of a node contains only the key Greater than Node key node . * Left and right subtrees must also be binary search trees . * Be careful : This topic and 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ identical * <p> * https://leetcode-cn.com/problems/convert-bst-to-greater-tree/ */
public class Solution {
int sum = 0;
public TreeNode convertBST(TreeNode root) {
if (root == null) {
return null;
}
convertBST(root.right);
sum += root.val;
root.val = sum;
convertBST(root.left);
return root;
}
}
边栏推荐
- Keepalive component cache does not take effect
- [groovy] compile time meta programming (compile time method interception | method interception in myasttransformation visit method)
- Model analysis of establishment time and holding time
- curlpost-php
- 激动人心,2022开放原子全球开源峰会报名火热开启
- 【文件IO的简单实现】
- SAP Spartacus home 页面读取 product 数据的请求的 population 逻辑
- Set data real-time update during MDK debug
- Cve-2017-11882 reappearance
- Leetcode 450 deleting nodes in a binary search tree
猜你喜欢
数据分析思维分析方法和业务知识——分析方法(二)
After 95, the CV engineer posted the payroll and made up this. It's really fragrant

Introduction of motor

The third season of ape table school is about to launch, opening a new vision for developers under the wave of going to sea

For a deadline, the IT fellow graduated from Tsinghua suddenly died on the toilet

Exciting, 2022 open atom global open source summit registration is hot

Analysis of the combination of small program technology advantages and industrial Internet
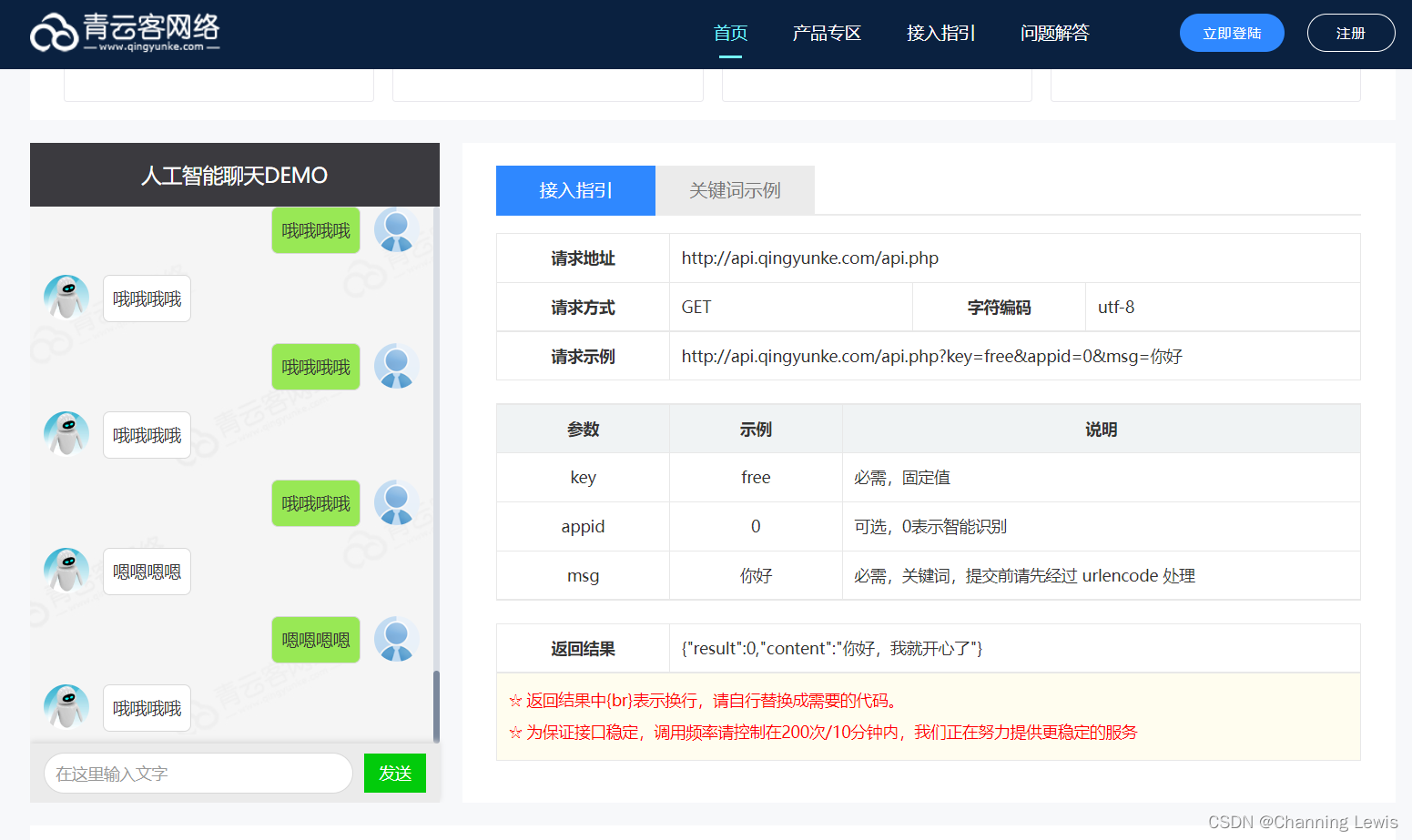
Free chat robot API
数据分析思维分析方法和业务知识——分析方法(三)
Model analysis of establishment time and holding time
随机推荐
程序员搞开源,读什么书最合适?
Problems and solutions of converting date into specified string in date class
[simple implementation of file IO]
云导DNS和知识科普以及课堂笔记
【线上小工具】开发过程中会用到的线上小工具合集
Questions about database: (5) query the barcode, location and reader number of each book in the inventory table
新手入门深度学习 | 3-6:优化器optimizers
Arduino hexapod robot
Leetcode:20220213 week race (less bugs, top 10% 555)
Power Query数据格式的转换、拆分合并提取、删除重复项、删除错误、转置与反转、透视和逆透视
After Luke zettlemoyer, head of meta AI Seattle research | trillion parameters, will the large model continue to grow?
MobileNet系列(5):使用pytorch搭建MobileNetV3并基于迁移学习训练
Dynamic programming -- linear DP
The population logic of the request to read product data on the sap Spartacus home page
anconda下载+添加清华+tensorflow 安装+No module named ‘tensorflow‘+KernelRestarter: restart failed,内核重启失败
Analysis of the combination of small program technology advantages and industrial Internet
Leetcode 44 Wildcard matching (2022.02.13)
Kotlin core programming - algebraic data types and pattern matching (3)
[groovy] compile time meta programming (AST syntax tree conversion with annotations | define annotations and use groovyasttransformationclass to indicate ast conversion interface | ast conversion inte
An understanding of & array names