当前位置:网站首页>1079 延迟的回文数 (20 分)
1079 延迟的回文数 (20 分)
2022-08-03 05:09:00 【破烂摆烂人】
给定一个 k+1 位的正整数 N,写成 a
k
⋯a
1
a
0
的形式,其中对所有 i 有 0≤a
i
<10 且 a
k
>0。N 被称为一个回文数,当且仅当对所有 i 有 a
i
=a
k−i
。零也被定义为一个回文数。
非回文数也可以通过一系列操作变出回文数。首先将该数字逆转,再将逆转数与该数相加,如果和还不是一个回文数,就重复这个逆转再相加的操作,直到一个回文数出现。如果一个非回文数可以变出回文数,就称这个数为延迟的回文数。(定义翻译自 https://en.wikipedia.org/wiki/Palindromic_number )
给定任意一个正整数,本题要求你找到其变出的那个回文数。
输入格式:
输入在一行中给出一个不超过1000位的正整数。
输出格式:
对给定的整数,一行一行输出其变出回文数的过程。每行格式如下
A + B = C
其中 A 是原始的数字,B 是 A 的逆转数,C 是它们的和。A 从输入的整数开始。重复操作直到 C 在 10 步以内变成回文数,这时在一行中输出 C is a palindromic number.;或者如果 10 步都没能得到回文数,最后就在一行中输出 Not found in 10 iterations.。
输入样例 1:
97152
输出样例 1:
97152 + 25179 = 122331
122331 + 133221 = 255552
255552 is a palindromic number.
输入样例 2:
196
输出样例 2:
196 + 691 = 887
887 + 788 = 1675
1675 + 5761 = 7436
7436 + 6347 = 13783
13783 + 38731 = 52514
52514 + 41525 = 94039
94039 + 93049 = 187088
187088 + 880781 = 1067869
1067869 + 9687601 = 10755470
10755470 + 07455701 = 18211171
Not found in 10 iterations.
#include <stdio.h>
#include <stdlib.h>
/* run this program using the console pauser or add your own getch, system("pause") or input loop */
int main(int argc, char *argv[]) {
char a[1010] , b[1010] = {
0} ;
scanf("%s",&a) ;
int i , j ;
for( i = 0 ; i < 10 ; i++ ){
//变成回文的步数
int k = strlen(a) - 1 , flag = 1 ;
for( j = 0 ; j < (k+1)/2 ; j++ ){
//判断是否为回文
if( a[j] != a[k-j] ){
flag = 0 ;
break ;
}
}
if( flag == 1 ){
printf("%s is a palindromic number.",a) ;
break ;
}else{
for( j = 0 ; j < k + 1 ; j++ ){
b[j] = a[k-j] ;
}
printf("%s + %s = ", a, b) ;
int sum , part = 0;
for( j = k ; j >= 0 ; j-- ){
sum = a[j] - '0' + b[j] - '0' + part;
a[j] = sum % 10 + '0';
part = sum / 10;
}
if(part){
memmove(a + 1, a, k + 2);
a[0] = part + '0';
}
printf("%s\n", a);
}
}
if( i == 10 ){
printf("Not found in 10 iterations.") ;
}
return 0;
}
边栏推荐
猜你喜欢
IO process thread -> thread -> day5
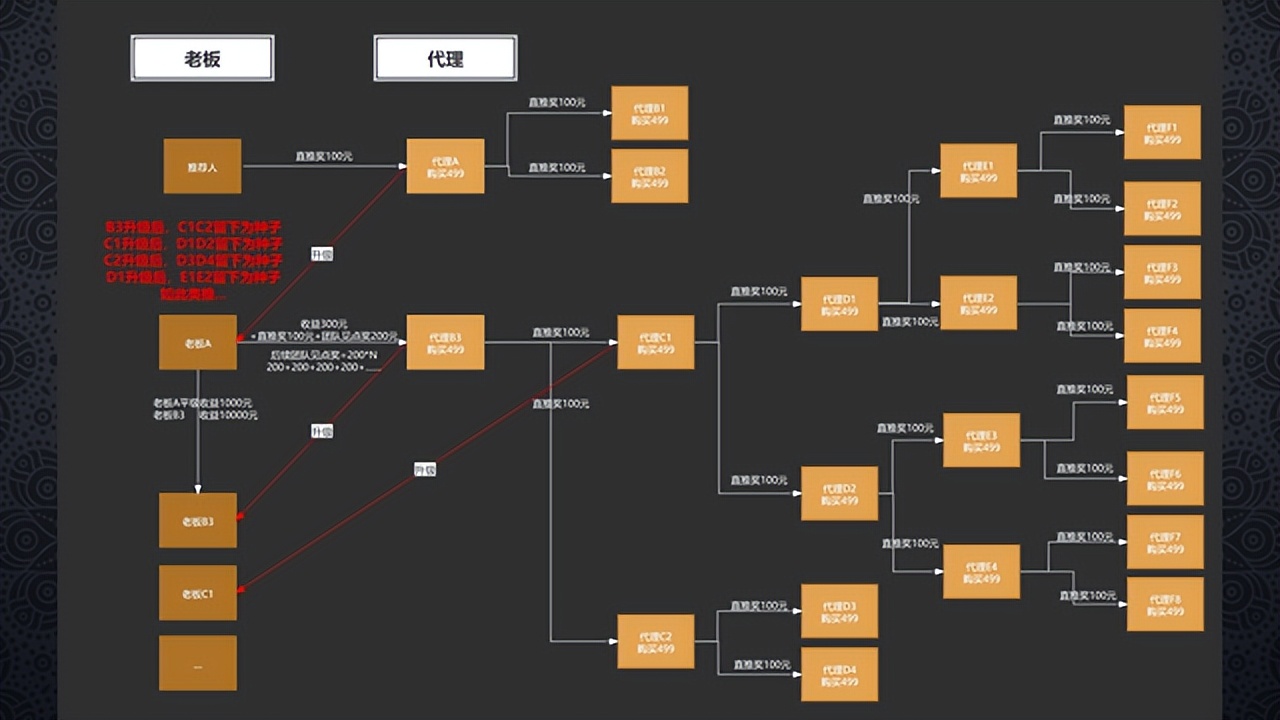
在竞争白热化的电商行业,链动2+1为什么还有企业在用
unity2D横板游戏教程6-敌人AI以及受击动画
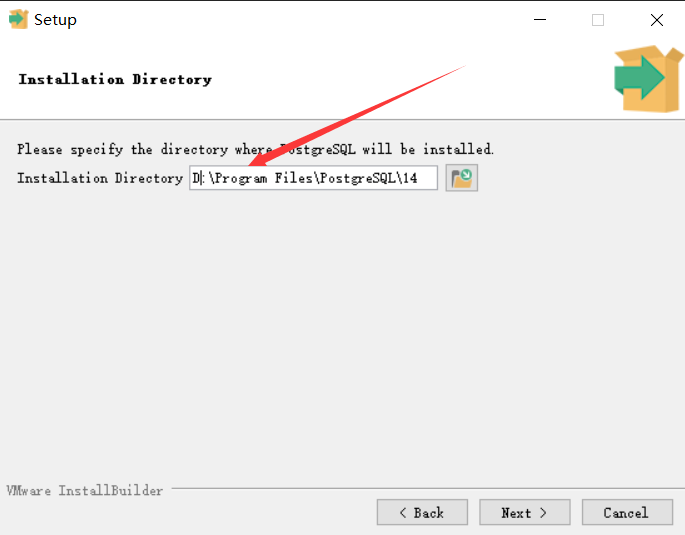
Install PostgreSQL on Windows

Interface test practice | Detailed explanation of the difference between GET / POST requests
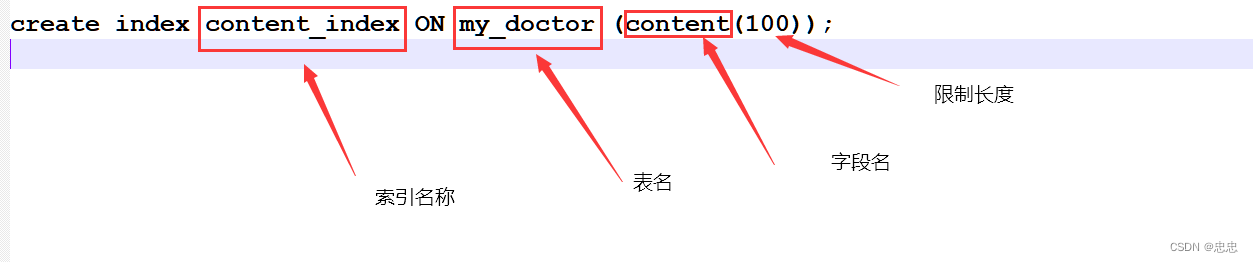
mysql 创建索引的三种方式
【HMS core】【Ads Kit】Huawei Advertising——Overseas applications are tested in China. Official advertisements cannot be displayed

typescript41-class类的私有修饰符
【Harmony OS】【ARK UI】ETS 上下文基本操作
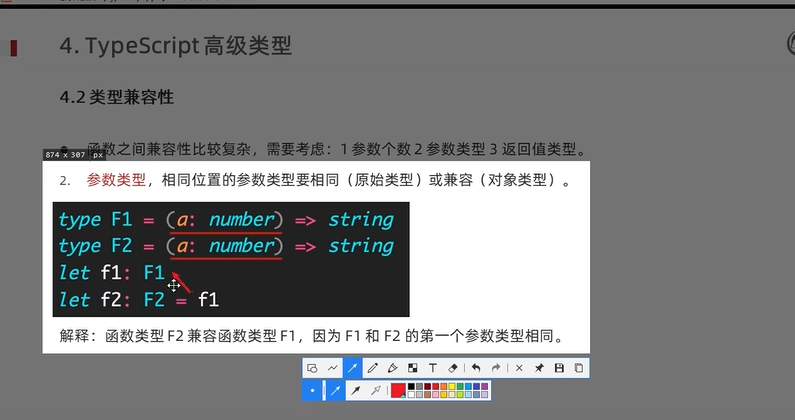
typescript47-函数之间的类型兼容性
随机推荐
接口测试实战| GET/POST 请求区别详解
社交电商:链动2+1模式,为什么能在电商行业生存那么久?
Windows 安装PostgreSQL
在线密码生成工具推荐
typescript43-类型兼容性说明
在树莓派上搭建属于自己的网页(1)
刚上线就狂吸70W粉,新型商业模式“分享购”来了,你知道吗?
Interface testing framework of actual combat (2) | interface request assertion
多肽介导PEG磷脂——靶向功能材料之DSPE-PEG-RGD/TAT/NGR/APRPG
How to prepare for the test interface test data
MCM box model modeling method and source analysis of atmospheric O3
WebSocket的实际应用
Fluorescent marker peptides FITC/AMC/FAM/Rhodamine TAMRA/Cy3 / Cy5 / Cy7 - Peptide
closures in js
Interface test practice | Detailed explanation of the difference between GET / POST requests
获取Ip工具类
Shell条件语句判断
GIS数据漫谈(五)— 地理坐标系统
【Harmony OS】【FAQ】鸿蒙问题合集1
自组织是管理者和成员的双向奔赴