当前位置:网站首页>Introduction of ArcGIS grid resampling method
Introduction of ArcGIS grid resampling method
2022-07-05 21:04:00 【GIS thinking】
Introduction to grid resampling method
Grid resampling is the process of assigning the pixel value or derived value of the input image to each pixel in the output image . The image mentioned here is grid data , Including grid (GRID) And image (IMAGE) Two types of . When the position of input image and output image ( After geometric transformation or projection setting and other operations ) Or pixel size ( Grid image resolution ) When something changes , Grid resampling is required .
Besides , Grid resampling is a common data processing method for grid data to deal with grid resolution matching in spatial analysis , For the convenience of analysis , Usually, different resolutions are converted to the same resolution through grid resampling . For a given spatial resolution of grid data , You can resample , Resample the grid data into larger pixels , That is, reduce the spatial resolution . This process will lose some details of the original high spatial resolution ; It can also be resampled into smaller pixels , But it will not add more information . Resample the multispectral remote sensing image with geospatial resolution into the same resolution as the panchromatic image with high spatial resolution , Then fuse the two images , The resulting image will have both high spectral resolution and high spatial resolution information , It can be used for topic extraction and Application , It is a common way of remote sensing data fusion .
Grid resampling mainly includes three methods : Nearest neighbor method 、 Bilinear interpolation and cubic convolution interpolation . The nearest neighbor method is to fill the nearest pixel value in the original image into the new image ; Bilinear interpolation and cubic convolution interpolation fill the pixel values near the original image into the new image by distance weighted average . These three resampling methods will be introduced in detail below .
Nearest neighbor method
The nearest neighbor method takes the nearest pixel value in the input grid data set as the input value , Assign the corresponding pixels to the output grid dataset .
The advantage of this method is that the original grid value will not be changed , And it's fast , But this method will have a displacement of half a pixel . It is suitable for discrete data representing classification or a certain topic , Such as land use 、 Vegetation type, etc .
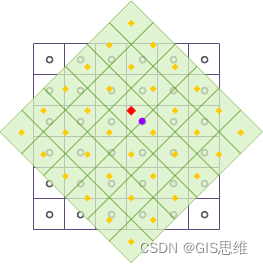
|
As shown in the figure above , After geometric transformations such as translation and rotation for grid data , Resample the output grid dataset , Adopt the nearest neighbor method . among , The black wireframe indicates the input grid dataset , A light green fill indicates the output grid dataset , The Red Square dot indicates the central position of a pixel in the output grid data set , Its pixel value will be recalculated . Find the center point of the pixel closest to the Red Square point , That is, the purple dots shown in the figure , Fill the pixel value represented by the purple dot into the Red Square dot , Complete the resampling of a grid pixel .
Bilinear interpolation
Bilinear interpolation is a method based on cubic linear interpolation , Will be input into 4 The nearest pixel (4 Neighborhood ) Calculate the new pixel value by weighted average of the pixel value of , And assign it to the corresponding pixel of the output grid dataset . among , The weight is determined by 4 The distance between the center of each pixel in the neighborhood and the interpolation point .
The resampling result of this method will be smoother than that of the nearest neighbor method , But it will change the original grid value . It is applicable to express the distribution of a certain phenomenon 、 Continuous data of topographic surface , Such as DEM、 Temperature or rainfall distribution 、 Slope, etc , These data are originally continuous surfaces obtained by interpolation of sampling points .
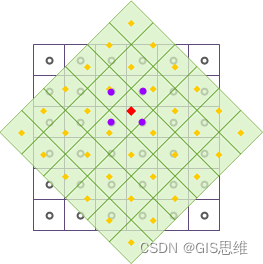
|
As shown in the figure above , After geometric transformations such as translation and rotation for grid data , Resample the output grid dataset , Bilinear interpolation method is adopted . among , The black wireframe indicates the input grid dataset , A light green fill indicates the output grid dataset , The Red Square dot indicates the central position of a pixel in the output grid data set , Its pixel value will be recalculated . Take the... Around the Red Square dot 4 Adjacent points , this 4 The center point of the adjacent points is the position indicated by the purple dot in the figure , Through the distance weighted average calculation , Fill the calculation result into the Red Square dot , Complete the resampling of a grid pixel .
Cubic convolution interpolation
Similar to bilinear interpolation , Cubic convolution interpolation is a method based on quintic polynomial interpolation , Will be input into 16 The nearest pixel (16 Neighborhood ) Calculate the new pixel value by weighted average of the pixel value of , And assign it to the corresponding pixel of the output grid dataset . among , The weight is determined by 16 The distance between the center point of each pixel in the neighborhood and the interpolation point .
Cubic convolution interpolation method obtains the best interpolation function by adding adjacent points , It can further improve the interpolation accuracy , The algorithm is more complex , Large amount of computation , Longer processing time . Because this method uses 16 The neighborhood is weighted , The processing result will be clearer , The boundary of grid data will be sharpened . This method will also change the original grid value , And it may exceed the value range of the input grid . It is suitable for resampling aerial photos and remote sensing images .
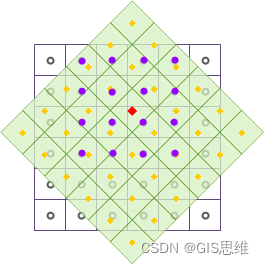
|
As shown in the figure above , After geometric transformations such as translation and rotation for grid data , Resample the output grid dataset , Using cubic convolution interpolation . among , The black wireframe indicates the input grid dataset , A light green fill indicates the output grid dataset , The Red Square dot indicates the central position of a pixel in the output grid data set , Its pixel value will be recalculated . Take the... Around the Red Square dot 16 Adjacent points , this 16 The center point of the adjacent points is the position indicated by the purple dot in the figure . Through the distance weighted average calculation , Fill the calculation result into the Red Square dot , Complete the resampling of a grid pixel .
Recommend learning
ArcGIS Model builder for (ModelBuilder) Video tutorial
ArcGIS10.X Video tutorial for getting started (GIS thinking )
ArcGIS Remote sensing image classification and results application video course
ArcPy Combined with the batch drawing of data-driven module
ArcGIS And Data Reviewer Spatial data quality inspection
GIS thinking GIS Series of technical courses

边栏推荐
- ArcGIS\QGIS无插件加载(无偏移)MapBox高清影像图
- Clion-MinGW编译后的exe文件添加ico图标
- 【案例】定位的运用-淘宝轮播图
- haas506 2.0开发教程 - 阿里云ota - pac 固件升级(仅支持2.2以上版本)
- Duchefa cytokinin dihydrozeatin (DHZ) instructions
- Sequence alignment
- LeetCode_哈希表_困难_149. 直线上最多的点数
- EN 438-7 laminated sheet products for building covering decoration - CE certification
- 实现浏览页面时校验用户是否已经完成登录的功能
- 100 cases of shell programming
猜你喜欢

研学旅游实践教育的开展助力文旅产业发展

Pytorch实战——MNIST数据集手写数字识别
The transformation based on vertx web sstore redis to realize the distributed session of vertx HTTP application
phpstudy小皮的mysql点击启动后迅速闪退,已解决
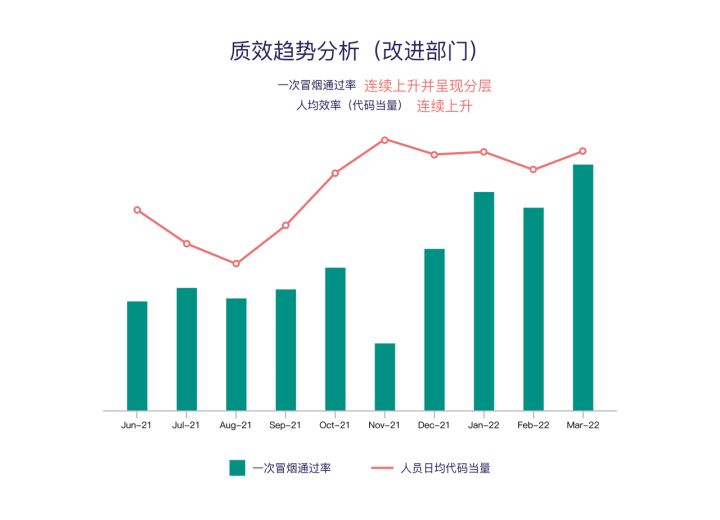
10000+ 代码库、3000+ 研发人员大型保险集团的研发效能提升实践

Using webassembly to operate excel on the browser side

Pytoch practice -- MNIST dataset handwritten digit recognition

Duchefa low melting point agarose PPC Chinese and English instructions
Clion configures Visual Studio (MSVC) and JOM multi-core compilation

EN 438-7 laminated sheet products for building covering decoration - CE certification
随机推荐
AITM 2-0003 水平燃烧试验
CLion配置visual studio(msvc)和JOM多核编译
matplotlib绘图润色(如何形成高质量的图,例如设如何置字体等)
leetcode:1755. 最接近目标值的子序列和
systemd-resolved 开启 debug 日志
sql系列(基础)-第二章 限制和排序数据
JS common method encapsulation
当用户登录,经常会有实时的下拉框,例如,输入邮箱,将会@qq.com,@163.com,@sohu.com
Which is the best online collaboration product? Microsoft loop, notion, flowus
2.<tag-哈希表, 字符串>补充: 剑指 Offer 50. 第一个只出现一次的字符 dbc
模式-“里氏替换原则”
The development of research tourism practical education helps the development of cultural tourism industry
ts 之 类的简介、构造函数和它的this、继承、抽象类、接口
When steam education enters personalized information technology courses
Specification of protein quantitative kit for abbkine BCA method
【案例】元素的显示与隐藏的运用--元素遮罩
请查收.NET MAUI 的最新学习资源
MYSQL IFNULL使用功能
Écrire une interface basée sur flask
Research and development efficiency improvement practice of large insurance groups with 10000 + code base and 3000 + R & D personnel