leetcode：1755. 最接近目标值的子序列和

题目来源

• leetcode：1755. 最接近目标值的子序列和

题目描述

class Solution {
    
public:
    int minAbsDifference(vector<int>& nums, int goal) {
    

    }
};

题目解析

分析数据量

在看题之前，我们先看下给出的数据量：$1<=nums.length<=40$，这意味着：

• 一方面，它几乎不太可能具有$O(N^2)、O(N^{2}logN)、O(N^3)$，这样的时间复杂度，因为[1，40]的数据范围显得太小了
• 另一方面，它也不可能具有$O(2^N)、O(N\ast 2^N)、O(3^N)$这样的时间复杂度，因为[1，40]的数据范围又太大了

一般来讲，数据量$n<=20$，这暗示着我们应该用一个指数级别的算法来解决，比如分治、回溯、dfs等，像哪些动态规划之类的通通pass。那么对于$n<=40$，唯一的可能性就是将40拆分成两个20，然后两边分别运行一个指数复杂度的解法

然后看下数据范围，好像有点大呀，动态规划pass

分析题意

然后再来看题。题目要求我们从数组中选出一些子集，经sum(子集) 最近接goal。

因为要求最接近，所以我们是肯定需要看尽所有的子集的。

枚举所有的子集可以用回溯的方法。

但是因为数据量$n<=40$，如果枚举全部子集那么复杂度为$2^{4}0$，肯定会超时，所以需要做一定的处理

补充

ps：关于“最接近目标值的子序列和”这一类问题：

• 如果数组长度特别大，但是值小，我们可以使用背包问题的方式来解决
• 但是如果数组长度不大，但是数值特别大的话，使用DFS。

dfs

class Solution {
    
    int point = 0; // 数组数据组合的指针（表示数组的下标）
    /** * @param nums 题目给出的数组 * @param start 数组的开始位置 * @param end 数组的结束位置 * @param sum 保存左侧组合的和（sum） * @param arr 保存数组组合的和 */
    void dfs(vector<int>& nums, int goal, int start, int sum, vector<int>& arr){
    
        arr[point++] = sum;
        for (int i = start; i < nums.size(); ++i) {
    
            dfs(nums, goal, i + 1, sum + nums[i], arr);
        }
    }
public:
    int minAbsDifference(vector<int>& nums, int goal) {
    
        int N = nums.size();
        int mid = N >> 1;
        point = 0;
        // 数据{ 5, -7, 3, 5 }==>左侧[5,-7] 右侧[5,-2]
        // 保存所有左侧数据的组合==>[0, -7, 5, -2] 左侧数据为(5,-7)
        std::vector<int> l(1 << 20);
        // 保存右侧所有数据的组合==>[0, 5, 3, 8] 右侧数据为(5,-2)
        std::vector<int> r(1 << 20);


        dfs(nums, 0, mid - 1, 0, l); // 枚举左侧所有组合
        point = 0;// 指针归0
        dfs(nums, mid, N - 1, 0, r);// 枚举右侧所有组合

        int ans = INT32_MAX;
        std::sort(l.begin(), l.end());
        std::sort(r.begin(), r.end());

        //组合左侧数据与右侧数据
        int left = 0, right = N - 1;
        for(int x : l){
    
            ans = std::min(ans, std::abs(goal - x));
        }
        for(int x : r){
    
            ans = std::min(ans, std::abs(goal - x));
        }
        while (left < N && right >= 0){
    
            int t = l[left] + r[right]; //临时保存左侧数据与右侧数据的组合
            ans = std::min(ans, std::abs(t - goal));
            if(t > goal){
    
                right--;
            }else{
    
                left++;
            }
        }

        return ans;
    }
};

暴力（超时）

枚举所有子序列

class Solution {
    
    int ans = INT32_MAX;

    void dfs(vector<int>& nums, int goal, int start, int sum){
    
        ans = std::min(ans, std::abs(sum - goal));
        for (int i = start; i < nums.size(); ++i) {
    
            dfs(nums, goal, i + 1, sum + nums[i]);  //注意这里是i+1......易错点
        }
    }
public:
    int minAbsDifference(vector<int>& nums, int goal) {
    
        if(nums.empty()){
    
            return goal;
        }

        dfs(nums, goal, 0, 0);
        return ans;
    }
};

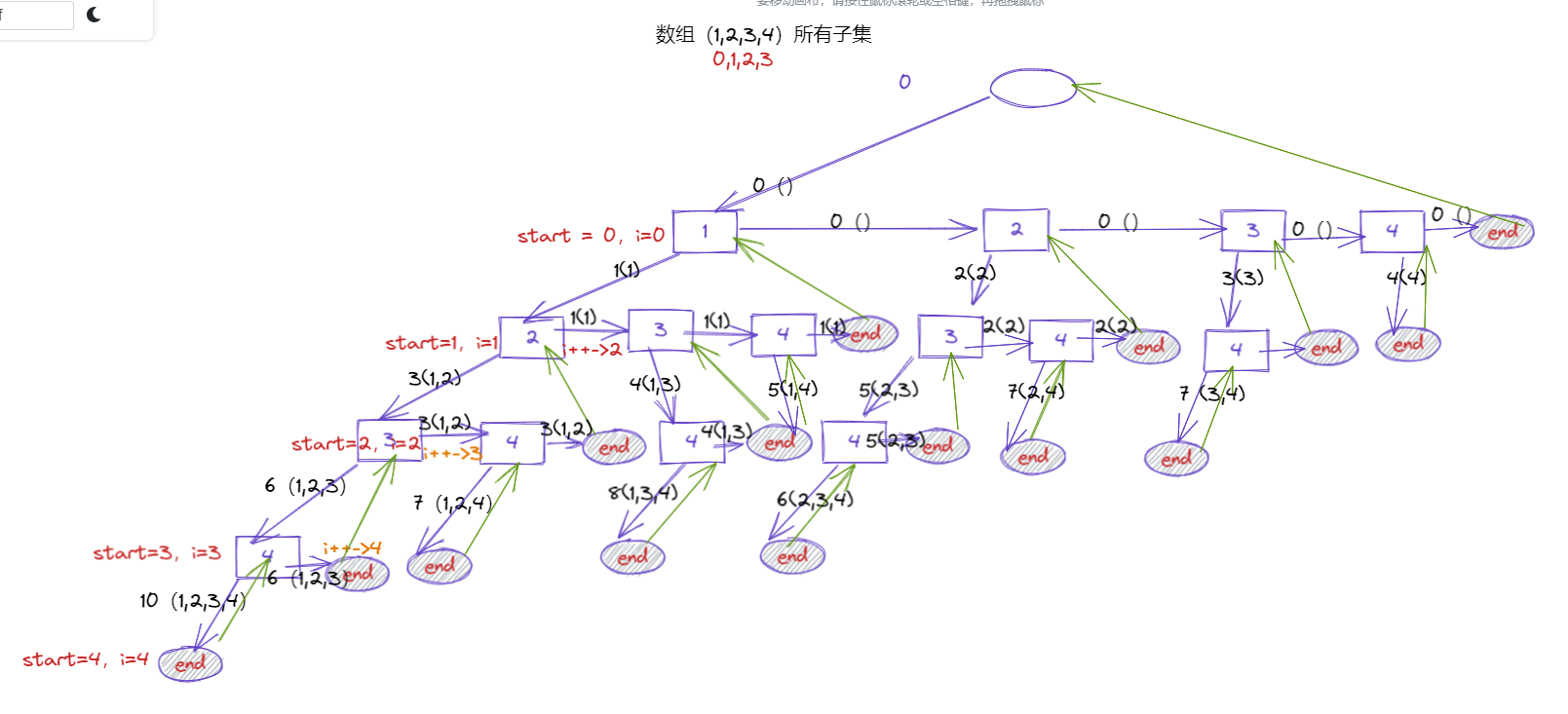
小结：数据范围 n :

• n <= 20, 可以暴力，2^20
• n <= 40, 不能直接暴力，但是可以对半来，20 * 2^20