当前位置:网站首页>E. Singhal and numbers (prime factor decomposition)
E. Singhal and numbers (prime factor decomposition)
2022-07-05 20:23:00 【Dimple】
https://codeforces.com/gym/102767/problem/E
The question
Give a number n, You can choose less than n As a factor of N.
- If N Prime number , So the answer is A + X N A + \frac{X}{N} A+NX;
- If N Is the sum , So the answer is B + X N B + \frac{X}{N} B+NX;
- If N by 1, So the answer is C + X N C + \frac{X}{N} C+NX.
ask , What is the minimum answer ?
Ideas
To minimize the answer , Be sure to find the largest prime factor , The largest combining factor .
Prime factor decomposition finds the maximum prime factor ,O( n \sqrt{n} n).
In order to find the maximum composite number , Sure First find the maximum factor :n / Minimum prime factor .
- If the maximum factor is prime , It means that there is no maximum combining factor .
- Otherwise, the maximum factor is the maximum resultant factor .
Note that the factor in this question should be less than n, So we can make a special judgment first n In the case of prime numbers .
Code
#include<bits/stdc++.h>
using namespace std;
#define Ios ios::sync_with_stdio(false),cin.tie(0)
const int N = 200010, mod = 1e9+7;
int T, n, m;
int a, b, c;
bool isPrim(int x){
if(x == 0 || x == 1) return 0;
for(int i=2;i<=x/i;i++)
{
if(x % i == 0) return 0;
}
return 1;
}
signed main(){
Ios;
cin >> T;
while(T--)
{
cin >> n;
cin >> a >> b >> c;
if(isPrim(n)){
cout << c + n << endl;
continue;
}
int mprim = -1, mcom = -1;
int minprim = -1;
int t = n;
for(int i=2;i<=t/i;i++)
{
if(t % i == 0)
{
while(t % i == 0) t/=i, mprim = i;
if(minprim == -1) minprim = i;
}
}
if(t != 1) mprim = t;
int min1 = 1e18, min2 = 1e18, min3 = 1e18;
min1 = a+n/mprim;
mcom = n/minprim;
if(!isPrim(mcom)) min2 = b+n/mcom;
min3 = c+n;
int ans = min(min(min1, min2), min3);
cout << ans << endl;
}
return 0;
}
边栏推荐
- Station B up builds the world's first pure red stone neural network, pornographic detection based on deep learning action recognition, Chen Tianqi's course progress of machine science compilation MLC,
- Guidelines for application of Shenzhen green and low carbon industry support plan in 2023
- Rainbow 5.7.1 supports docking with multiple public clouds and clusters for abnormal alarms
- Fundamentals - configuration file analysis
- B站UP搭建世界首个纯红石神经网络、基于深度学习动作识别的色情检测、陈天奇《机器学编译MLC》课程进展、AI前沿论文 | ShowMeAI资讯日报 #07.05
- MySql的root密码忘记该怎么找回
- Introduction to dead letter queue (two consumers, one producer)
- Model method
- 3.3、项目评估
- 19 Mongoose模块化
猜你喜欢
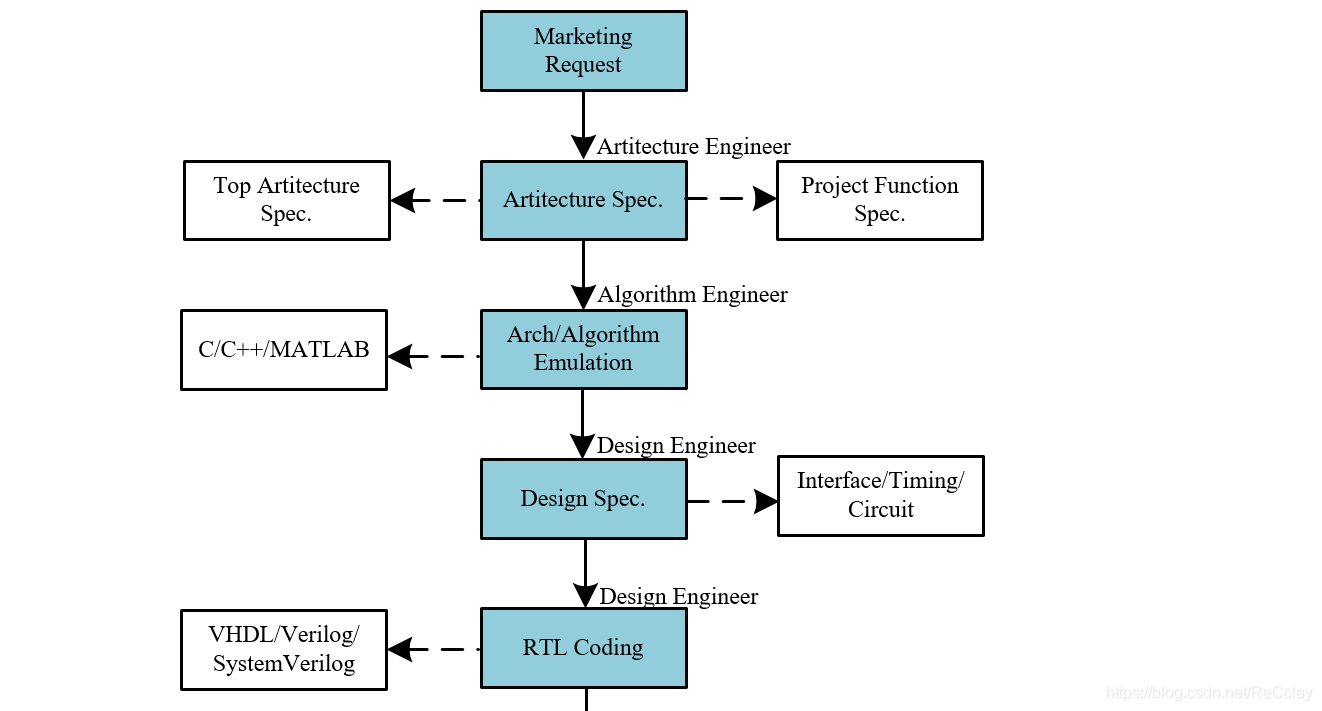
【数字IC验证快速入门】3、数字IC设计全流程介绍
【数字IC验证快速入门】6、Questasim 快速上手使用(以全加器设计与验证为例)
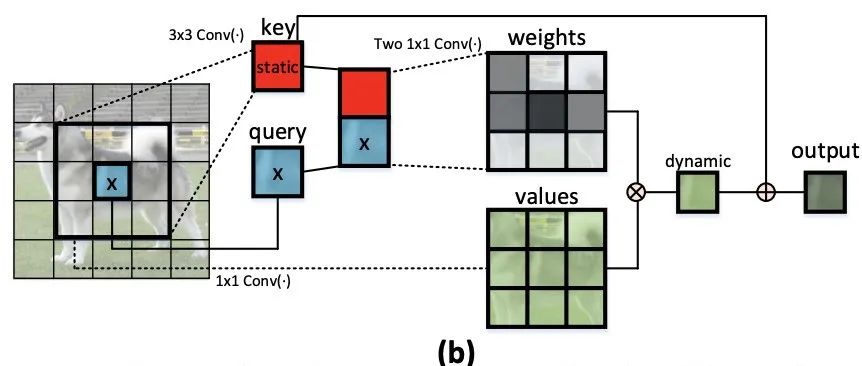
无卷积骨干网络:金字塔Transformer,提升目标检测/分割等任务精度(附源代码)...
![[quick start of Digital IC Verification] 9. Finite state machine (FSM) necessary for Verilog RTL design](/img/32/a156293f145417eeae8d93c539ca55.png)
[quick start of Digital IC Verification] 9. Finite state machine (FSM) necessary for Verilog RTL design

解决php无法将string转换为json的办法

Practical demonstration: how can the production research team efficiently build the requirements workflow?
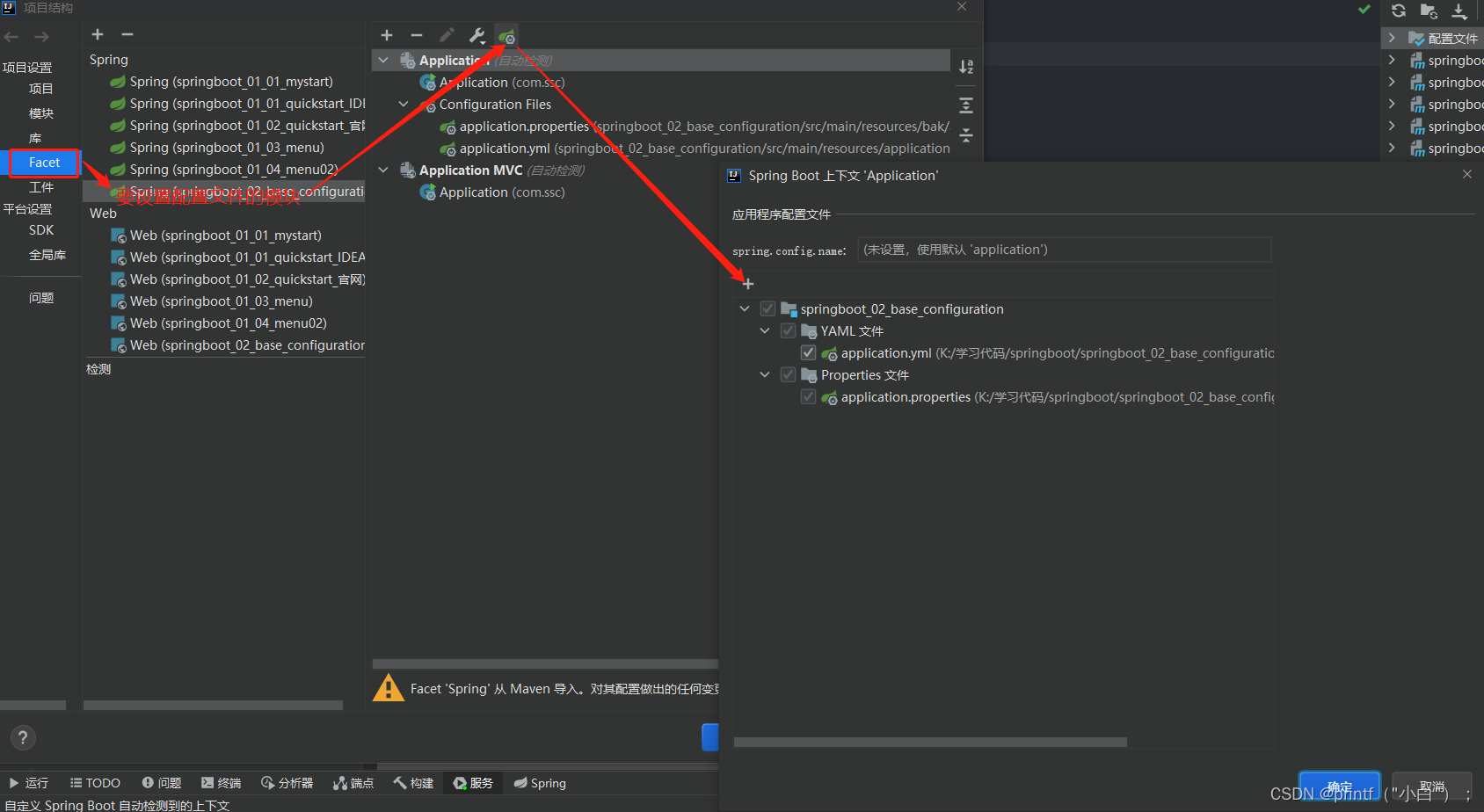
基础篇——配置文件解析
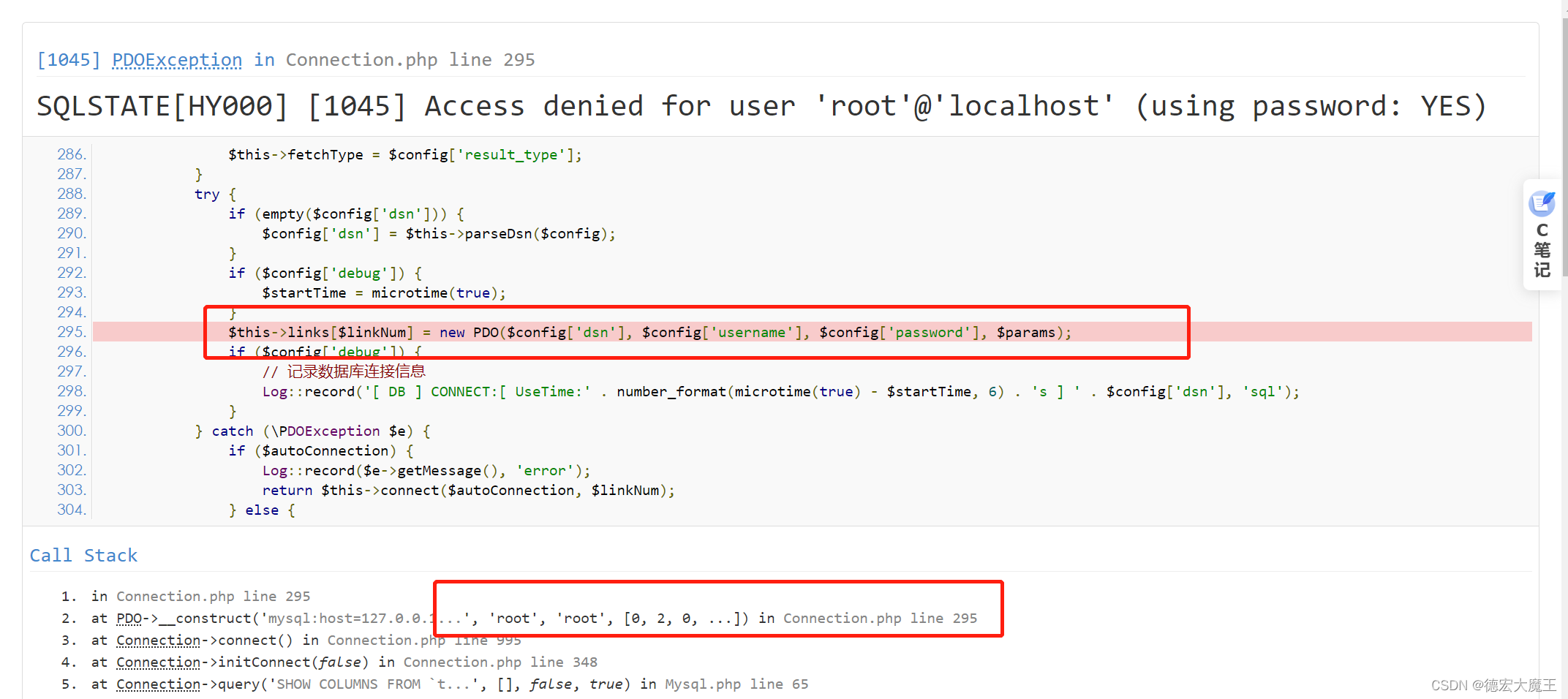
解决Thinkphp框架应用目录下数据库配置信息修改后依然按默认方式连接
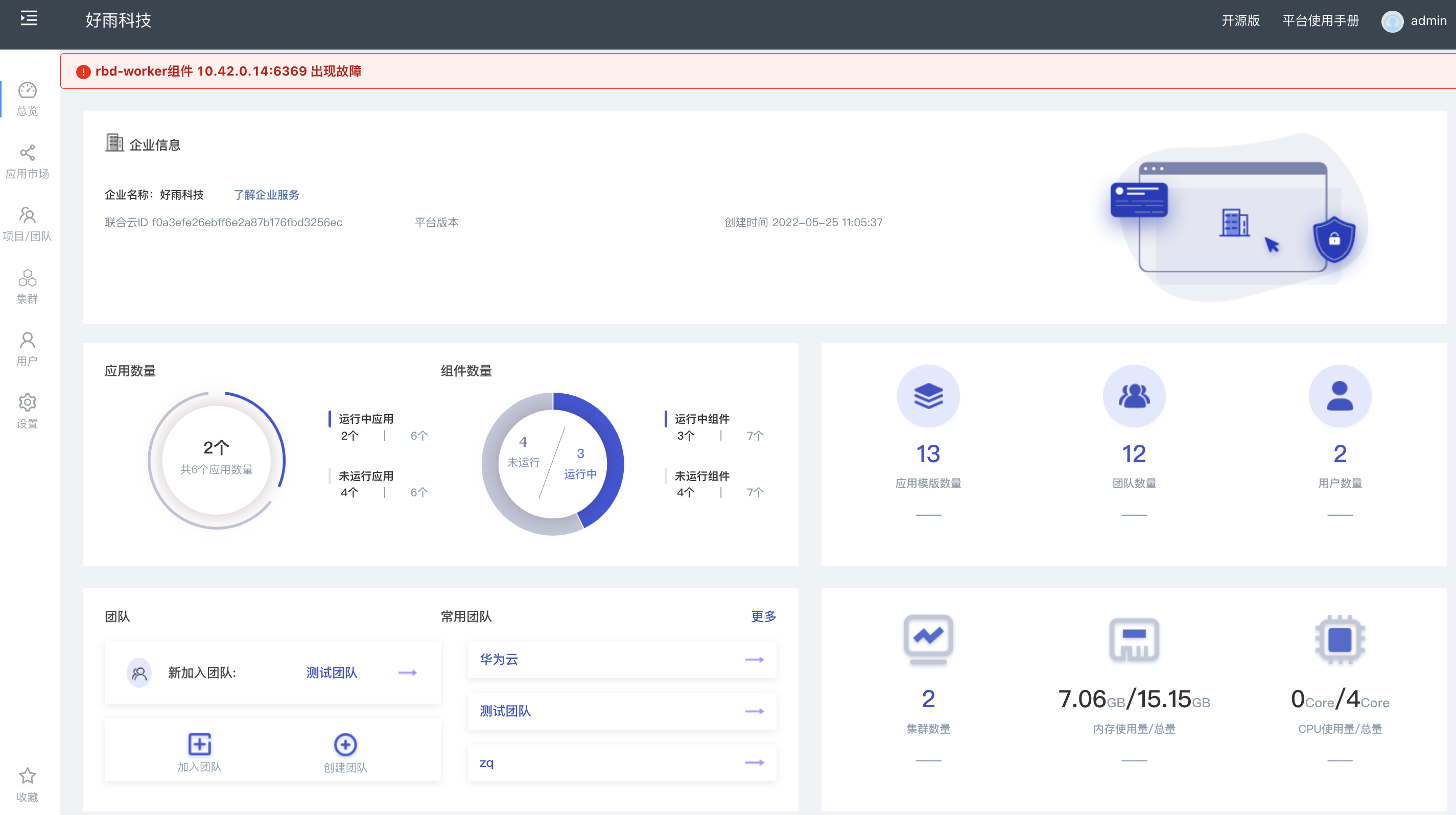
Rainbond 5.7.1 支持对接多家公有云和集群异常报警
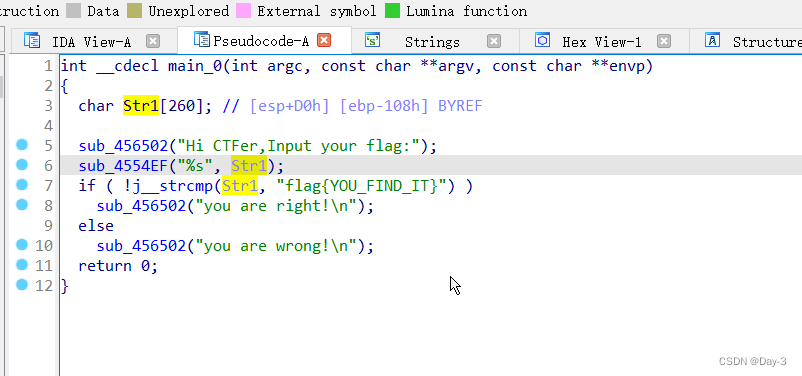
CTF reverse Foundation
随机推荐
小程序代码的构成
19 mongoose modularization
插值查找的简单理解
点云文件的.dat文件读取保存
Codeforces Round #804 (Div. 2) - A, B, C
【数字IC验证快速入门】1、浅谈数字IC验证,了解专栏内容,明确学习目标
Sort and projection
ICTCLAS word Lucene 4.9 binding
Oracle-表空间管理
js实现禁止网页缩放(Ctrl+鼠标、+、-缩放有效亲测)
零道云新UI设计中
【c语言】归并排序
信息学奥赛一本通 1340:【例3-5】扩展二叉树
July 4, 2022 - July 10, 2022 (UE4 video tutorial MySQL)
Leetcode(347)——前 K 个高频元素
CVPR 2022 | 常见3D损坏和数据增强
小程序全局配置
How to choose a good external disk platform, safe and formal?
1: Citation;
计算lnx的一种方式