当前位置:网站首页>[daily question] 241 Design priorities for operational expressions
[daily question] 241 Design priorities for operational expressions
2022-07-02 19:51:00 【Wang Liuliu's it daily】
241. Design priorities for operation expressions
Refer to the explanation of the question :https://leetcode.cn/problems/different-ways-to-add-parentheses/solution/wei-yun-suan-biao-da-shi-she-by-jiang-hu-0pf0/
- recursive
Follow the string as The operator Split into two sub expressions , The result set of the two sub expressions is currently op The operation of , Assemble into a new result set , For each op The final answer is the sum of the result sets obtained by segmentation respectively . And the subexpression is the same problem , May adopt recursive Calculate , It will eventually recurse to a digit On .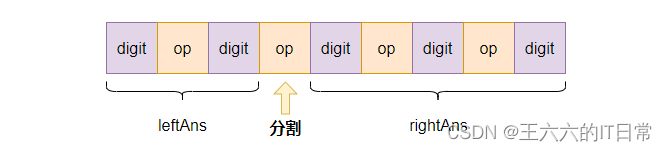
class Solution {
public List<Integer> diffWaysToCompute(String expression) {
// The expression is empty
if (expression == null || expression.length() == 0) {
return new ArrayList<>();
}
char[] chars = expression.toCharArray();
List<Integer> ans = new ArrayList<>();
for (int i = 0; i < chars.length; i++) {
char aChar = chars[i];
// If the current character is an operator , That is to say op, Segmentation
if (!Character.isDigit(aChar)) {
// Recursively get the result set of the left and right expressions
List<Integer> leftList = diffWaysToCompute(expression.substring(0, i));
List<Integer> rightList = diffWaysToCompute(expression.substring(i + 1));
// All the results of the two result sets are op operation
for (Integer left : leftList) {
for (Integer right : rightList) {
if (aChar == '+') {
ans.add(left + right);
} else if (aChar == '-') {
ans.add(left - right);
} else {
ans.add(left * right);
}
}
}
}
}
// Result set is empty , Prove that the string is a number , Add numbers to the result set
if (ans.isEmpty()) {
ans.add(Integer.valueOf(expression));
}
return ans;
}
}
- Dynamic programming
Because the final answer is a sub question ( subexpression ) The answer of , Therefore, dynamic programming can be adopted , Divide the problem into a sub problem to solve .
First, we divide the string into digit、op、digit、op、digit、op、digit… This sequence , And we know that the length of the sequence is an odd number , So the minimum length of the subproblem is 3( The length is 1 Of digit There is no need to calculate ), That's one op The operation requires at least three elements ( Two digit And a op), The length of the next sub problem is the current sub problem +2( Add one more op And a digit), So we can start from the minimum length of 3 Solve the maximum length solution step by step .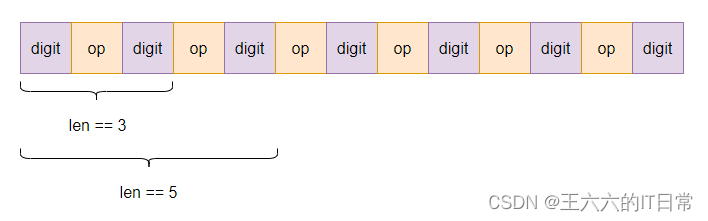
class Solution {
public List<Integer> diffWaysToCompute(String expression) {
List<Object> ops = new ArrayList<>();
// Split string into digit、op、digit、op、digit...... This sequence
for (int i = 0; i < expression.length(); ) {
if (!Character.isDigit(expression.charAt(i))) {
// Add operator
ops.add(expression.charAt(i));
i++;
} else {
// Add numbers
int digit = 0;
while (i < expression.length() && Character.isDigit(expression.charAt(i))) {
digit = digit * 10 + expression.charAt(i) - '0';
i++;
}
ops.add(digit);
}
}
//dp[i][j] From i To j Sub problem ( subexpression ) All the answers
List<Integer>[][] dp = new List[ops.size()][ops.size()];
for (int i = 0; i < ops.size(); i++) {
for (int j = 0; j < ops.size(); j++) {
dp[i][j] = new ArrayList<>();
}
}
// At the beginning , be-all digit They are themselves and the numbers are stored across , And the position is fixed in even digits (0,2,4...) therefore +2
//eg:digit、op、digit、op、digit......
for (int i = 0; i < ops.size(); i += 2) {
dp[i][i].add((int) ops.get(i));
}
// From the length to 3 Start to calculate the subproblem of
for (int len = 3; len <= ops.size(); len += 2) {
// The left boundary starts from 0 Start
for (int left = 0; left + len <= ops.size(); left += 2) {
// Right border
int right = left + len - 1;
// according to op Split the left and right sub expressions +2 It means next op
for (int k = left + 1; k < right; k += 2) {
List<Integer> leftAns = dp[left][k - 1];
List<Integer> rightAns = dp[k + 1][right];
// Merge the result sets of the left and right sub expressions
for (int num1 : leftAns) {
for (int num2 : rightAns) {
char op = (char) ops.get(k);
if (op == '+') {
dp[left][right].add(num1 + num2);
} else if (op == '-') {
dp[left][right].add(num1 - num2);
} else if (op == '*') {
dp[left][right].add(num1 * num2);
}
}
}
}
}
}
return dp[0][ops.size() - 1];
}
}
- DFS
Reference resources :https://leetcode.cn/problems/different-ways-to-add-parentheses/solution/by-ac_oier-z07i/
class Solution {
char[] cs;
public List<Integer> diffWaysToCompute(String s) {
cs = s.toCharArray();
return dfs(0, cs.length - 1);
}
List<Integer> dfs(int l, int r) {
List<Integer> ans = new ArrayList<>();
for (int i = l; i <= r; i++) {
if (cs[i] >= '0' && cs[i] <= '9') continue;
List<Integer> l1 = dfs(l, i - 1), l2 = dfs(i + 1, r);
for (int a : l1) {
for (int b : l2) {
int cur = 0;
if (cs[i] == '+') cur = a + b;
else if (cs[i] == '-') cur = a - b;
else cur = a * b;
ans.add(cur);
}
}
}
if (ans.isEmpty()) {
int cur = 0;
for (int i = l; i <= r; i++) cur = cur * 10 + (cs[i] - '0');
ans.add(cur);
}
return ans;
}
}
边栏推荐
- Function high order curry realization
- AcWing 1129. 热浪 题解(最短路—spfa)
- 451 implementation of memcpy, memmove and memset
- What is the Bluetooth chip ble, how to select it, and what is the path of subsequent technology development
- JS how to get integer
- LeetCode 0871. Minimum refueling times - similar to poj2431 jungle adventure
- 勵志!大凉山小夥全獎直博!論文致謝看哭網友
- AcWing 341. 最优贸易 题解 (最短路、dp)
- Getting started with typescript
- 为什么我对流程情有独钟?
猜你喜欢

JASMINER X4 1U深度拆解,揭开高效省电背后的秘密

Detailed tutorial on installing stand-alone redis

AcWing 903. 昂贵的聘礼 题解(最短路—建图、dijkstra)

Refactoring: improving the design of existing code (Part 1)

Registration opportunity of autowiredannotationbeanpostprocessor under annotation development mode
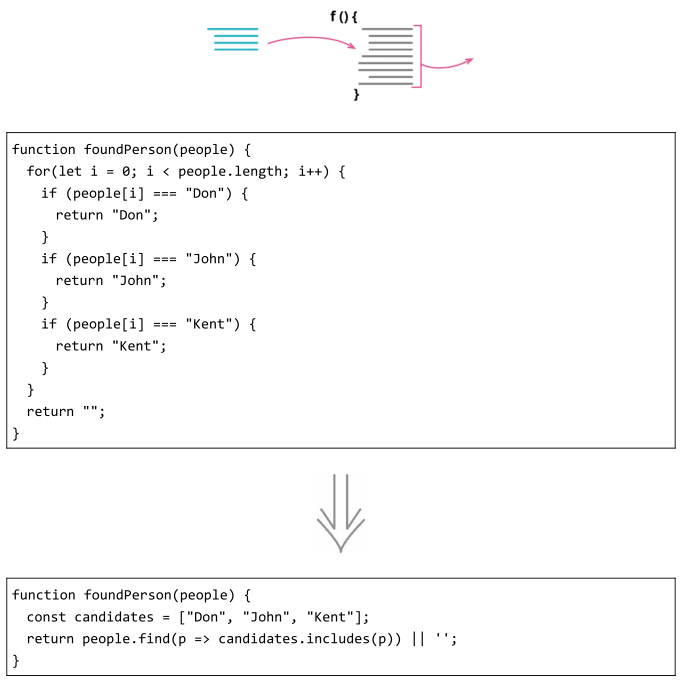
Refactoring: improving the design of existing code (Part 2)
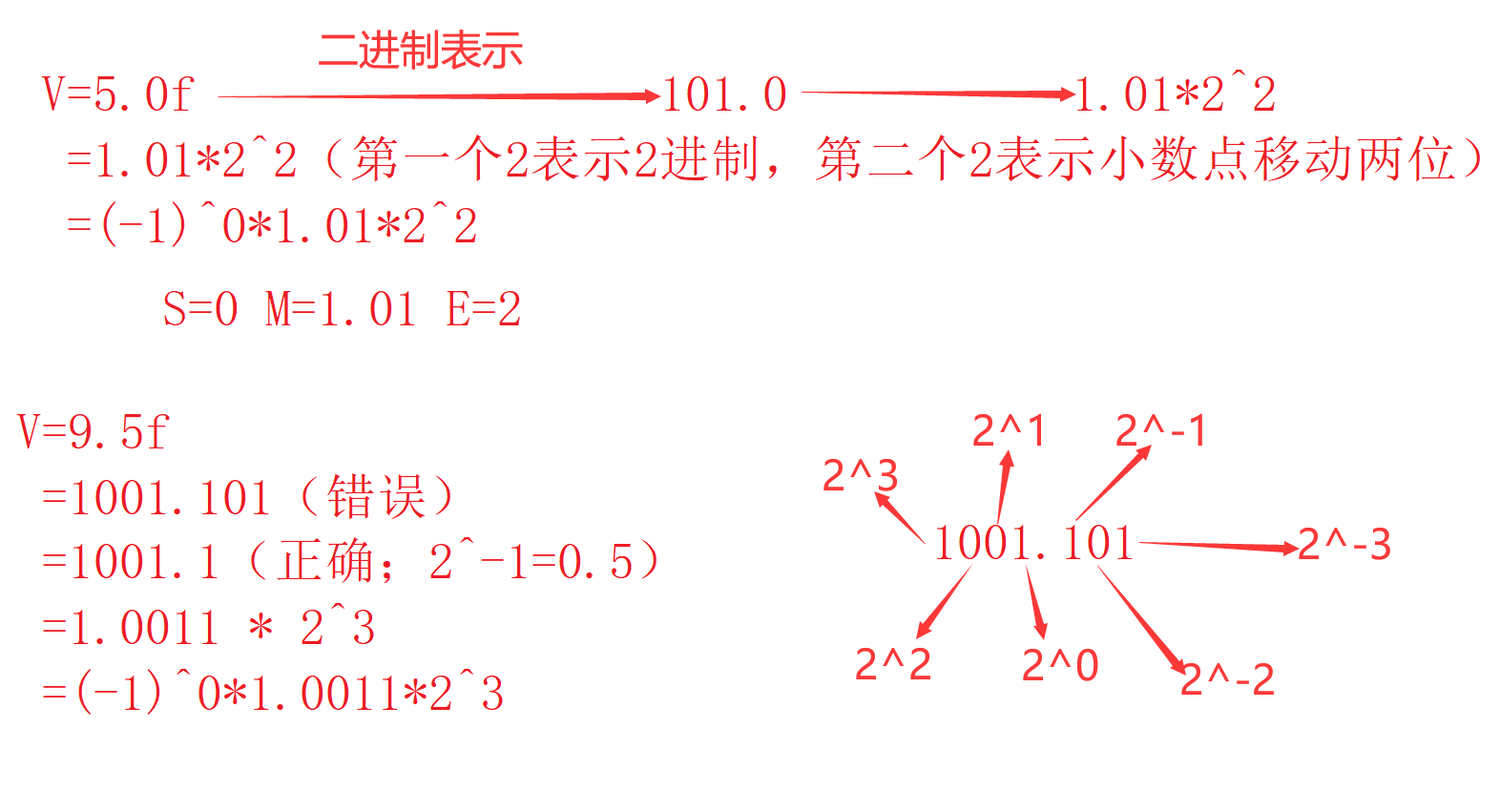
程序猿入门攻略(十二)——数据的存储

Génération automatique de fichiers d'annotation d'images vgg
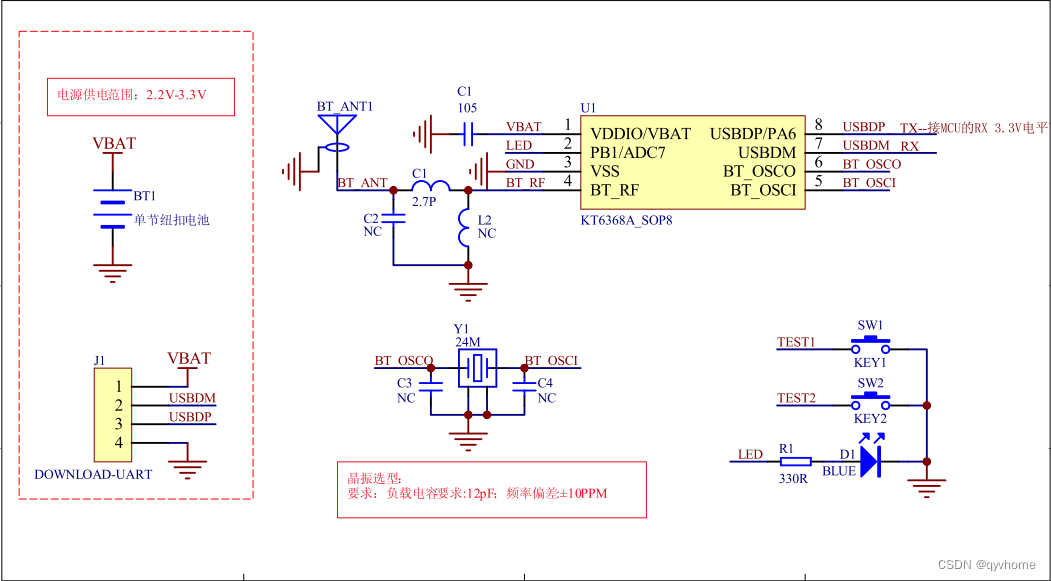
What is the Bluetooth chip ble, how to select it, and what is the path of subsequent technology development

Educational codeforces round 129 (rated for Div. 2) supplementary problem solution
随机推荐
编写完10万行代码,我发了篇长文吐槽Rust
开始练习书法
453-atoi函数的实现
多端小程序开发有什么好处?覆盖百度小程序抖音小程序微信小程序开发,抢占多平台流量红利
Notes on hardware design of kt148a voice chip IC
Golang concurrent programming goroutine, channel, sync
Implementation of 453 ATOI function
Postman下载安装
JASMINER X4 1U深度拆解,揭开高效省电背后的秘密
Reading notes of "the way to clean structure" (Part 2)
《MongoDB入门教程》第03篇 MongoDB基本概念
AcWing 1135. Happy New Year (shortest path + search)
Istio deployment: quickly start microservices,
中缀表达式转换为后缀表达式(C语言代码+详解)
AcWing 1129. Heat wave solution (shortest path SPFA)
多态的理解以及作用
自動生成VGG圖像注釋文件
SQLite 3.39.0 release supports right external connection and all external connection
pxe装机「建议收藏」
Use cheat engine to modify money, life and stars in Kingdom rush