当前位置:网站首页>九度 1480:最大上升子序列和(动态规划思想求最值)
九度 1480:最大上升子序列和(动态规划思想求最值)
2022-07-05 10:13:00 【全栈程序员站长】
一个数的序列bi,当b1 < b2 < … < bS的时候,我们称这个序列是上升的。对于给定的一个序列(a1, a2, …,aN),我们可以得到一些上升的子序列(ai1, ai2, …, aiK),这里1 <= i1 < i2 < … < iK <= N。比如,对于序列(1, 7, 3, 5, 9, 4, 8),有它的一些上升子序列,如(1, 7), (3, 4, 8)等等。这些子序列中序列和最大为18,为子序列(1, 3, 5, 9)的和.
你的任务,就是对于给定的序列,求出最大上升子序列和。注意,最长的上升子序列的和不一定是最大的,比如序列(100, 1, 2, 3)的最大上升子序列和为100,而最长上升子序列为(1, 2, 3)。
思路
1.dp[i] 表示以 i 结尾的最大上升序列
dp[i] = max(dp[j]) + value[i]
2. 最长上升子序列和最大上升子序列没有关系
3. 这题的思路和最大连续子数组一样
代码
#include <iostream> #include <stdio.h>
using namespace std; int dp[1001]; int val[1001]; int n; int main() { while(scanf("%d", &n) != EOF ) { for(int i = 0; i < n; i ++) scanf("%d", val+i); dp[0] = val[0]; for(int i = 1; i < n; i ++) { dp[i] = val[i]; for(int j = 0; j < i; j ++) { if(val[j] >= val[i]) continue; dp[i] = max(dp[i], dp[j]+val[i]); } } int resval = 0; for(int i = 0; i < n; i ++) resval = max(resval, dp[i]); cout << resval << endl; } return 0; }发布者:全栈程序员栈长,转载请注明出处:https://javaforall.cn/109896.html原文链接:https://javaforall.cn
边栏推荐
- In wechat applet, after jumping from one page to another, I found that the page scrolled synchronously after returning
- 小程序中自定义行内左滑按钮,类似于qq和wx消息界面那种
- Swift uses userdefaults and codable to save an array of class objects or structure instances
- LiveData 面试题库、解答---LiveData 面试 7 连问~
- The horizontally scrolling recycleview displays five and a half on one screen, lower than the average distribution of five
- [dark horse morning post] Luo Yonghao responded to ridicule Oriental selection; Dong Qing's husband Mi Chunlei was executed for more than 700million; Geely officially acquired Meizu; Huawei releases M
- Interview: how does the list duplicate according to the attributes of the object?
- B站大量虚拟主播被集体强制退款:收入蒸发,还倒欠B站;乔布斯被追授美国总统自由勋章;Grafana 9 发布|极客头条...
- Apple 5g chip research and development failure? It's too early to get rid of Qualcomm
- DDOS攻击原理,被ddos攻击的现象
猜你喜欢

A large number of virtual anchors in station B were collectively forced to refund: revenue evaporated, but they still owe station B; Jobs was posthumously awarded the U.S. presidential medal of freedo

伪类元素--before和after
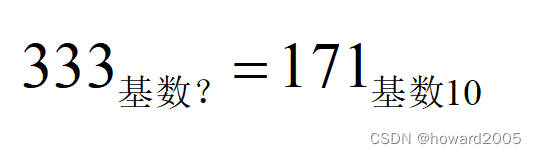
《天天数学》连载58:二月二十七日
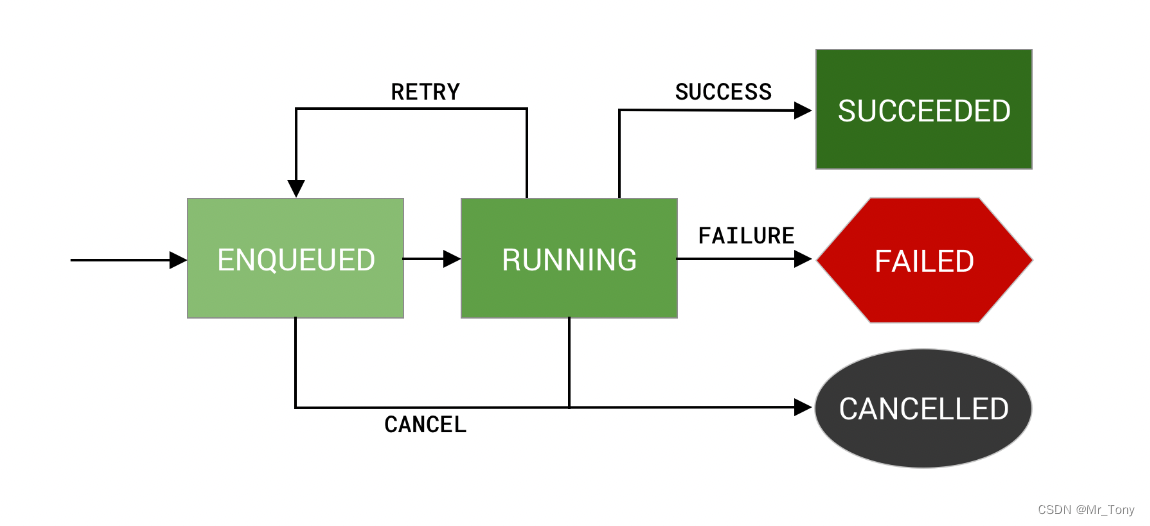
WorkManager的学习二
![[论文阅读] CKAN: Collaborative Knowledge-aware Atentive Network for Recommender Systems](/img/6c/5b14f47503033bc2c85a259a968d94.png)
[论文阅读] CKAN: Collaborative Knowledge-aware Atentive Network for Recommender Systems
Universal double button or single button pop-up

Advanced opencv:bgr pixel intensity map

如何写出高质量的代码?
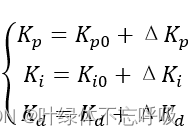
Design and Simulation of fuzzy PID control system for liquid level of double tank (matlab/simulink)
Redis如何实现多可用区?
随机推荐
mongoDB副本集
【JS】数组降维
The Alipay in place function can't be found, and the Alipay in place function is offline
What is the most suitable book for programmers to engage in open source?
Design and Simulation of fuzzy PID control system for liquid level of double tank (matlab/simulink)
Glide advanced level
Atcoder beginer contest 254 "e BFS" f st table maintenance differential array GCD "
Timed disappearance pop-up
MySQL digital type learning notes
@JsonAdapter注解使用
SAP ui5 objectpagelayout control usage sharing
How to plan the career of a programmer?
C function returns multiple value methods
"Everyday Mathematics" serial 58: February 27
5G NR系统架构
How can non-technical departments participate in Devops?
Click the picture in the mobile browser and the picture will not pop up
Qt实现json解析
How can PostgreSQL CDC set a separate incremental mode, debezium snapshot. mo
到底谁才是“良心”国产品牌?