当前位置:网站首页>General process of machine learning training and parameter optimization (discussion)
General process of machine learning training and parameter optimization (discussion)
2022-07-06 02:13:00 【Min fan】
Abstract : In practical machine learning applications , Not only model training , Also control the input parameters . This paper describes the general process , For reference only .
1. Training machine learning models
For an input of m m m Features , Output as a decision indicator , Machine learning models can be built
f : R m → R (1) f: \mathbb{R}^m \to \mathbb{R} \tag{1} f:Rm→R(1)
among R \mathbb{R} R Is a set of real numbers . If different features have their own value range , Then the machine learning model can be expressed as
f : ∏ i = 1 m V i → R (2) f: \prod_{i=1}^m \mathbf{V}_i \to \mathbb{R} \tag{2} f:i=1∏mVi→R(2)
among V i \mathbf{V}_i Vi It's No i i i Value range of features .
Simplicity , Only... Is discussed below (1) Model corresponding to formula .
Given to contain n n n Characteristic matrix of instances X = [ x 1 , … , x n ] T ∈ R n × m \mathbf{X} = [\mathbf{x}_1, \dots, \mathbf{x}_n]^{\mathrm{T}} \in \mathbb{R}^{n \times m} X=[x1,…,xn]T∈Rn×m And the corresponding label vector Y ∈ R n \mathbf{Y} \in \mathbb{R}^n Y∈Rn, The optimization objective of machine learning can generally be expressed as
min f L ( f ( X ) , Y ) + R ( f ) (3) \min_f \mathcal{L}(f(\mathbf{X}), \mathbf{Y}) + R(f) \tag{3} fminL(f(X),Y)+R(f)(3)
among f ( X ) = [ f ( x 1 ) , … , f ( x n ) ] f(\mathbf{X}) = [f(\mathbf{x}_1), \dots, f(\mathbf{x}_n)] f(X)=[f(x1),…,f(xn)] Vector for predicted tags , R ( f ) R(f) R(f) by f f f Regular term of parameter in . If the optimization goal is a convex function , Then the gradient descent method can be used to quickly find the optimal solution . For regular terms :
- If f f f For a linear model , The regular can be 1 norm 、2 norm 、 Kernel norm, etc . Its function is to prevent over fitting .
- If f f f For a neural network model , You can use the dropout And other technologies to prevent over fitting .
2. Parameter optimization method
For some practical problems , Some of the input characteristics are objective , Some are controllable . No loss of generality , Before order m 1 m_1 m1 The first feature is objective , after m 2 m_2 m2 Three features are controllable ( So we also call it parameter ), m 1 + m 2 = m m_1 + m_2 = m m1+m2=m. Suppose a reliable machine learning model has been trained through a large amount of data f f f, And we expect to maximize the decision indicators . Given the objective eigenvector x b ∈ R m 1 \mathbf{x}_b \in \mathbb{R}^{m_1} xb∈Rm1, The objective function of parameter optimization is
arg max x u ∈ R m 2 f ( x b ∥ x u ) (4) \argmax_{\mathbf{x_u} \in \mathbb{R}^{m_2}} f(\mathbf{x}_b \| \mathbf{x}_u)\tag{4} xu∈Rm2argmaxf(xb∥xu)(4)
among ∥ \| ∥ Indicates the vector splicing operation .
- If f f f Each controllable feature is a convex function , Then the optimal parameters can be obtained by gradient descent and other methods .
- If f f f The controllable features are not a convex function , Then some bionic algorithms can be used to optimize the parameters .
- If the controllable features are enumerated, the cardinality of the definition domain is not large , Then the optimal parameters can be obtained directly by the exhaustive method . example : Controllable features include 5 individual , Everyone with a 10 Possible values , From the 1 0 5 10^5 105 The optimal parameter vector is obtained from three parameter combinations , It only takes a few seconds to calculate .
边栏推荐
- Folio. Ink is a free, fast and easy-to-use image sharing tool
- Grabbing and sorting out external articles -- status bar [4]
- D22:indeterminate equation (indefinite equation, translation + problem solution)
- NiO related knowledge (II)
- 2022 PMP project management examination agile knowledge points (8)
- 【网络攻防实训习题】
- The ECU of 21 Audi q5l 45tfsi brushes is upgraded to master special adjustment, and the horsepower is safely and stably increased to 305 horsepower
- Redis key operation
- How to improve the level of pinduoduo store? Dianyingtong came to tell you
- 更改对象属性的方法
猜你喜欢
![抓包整理外篇——————状态栏[ 四]](/img/1e/2d44f36339ac796618cd571aca5556.png)
抓包整理外篇——————状态栏[ 四]
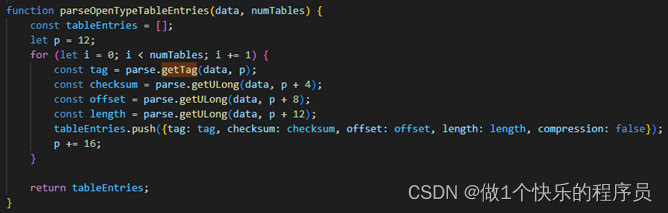
Extracting key information from TrueType font files
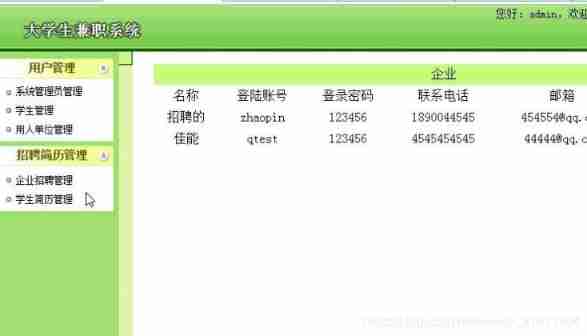
Computer graduation design PHP part-time recruitment management system for College Students
数据工程系列精讲(第四讲): Data-centric AI 之样本工程
![[ssrf-01] principle and utilization examples of server-side Request Forgery vulnerability](/img/43/a8f302eb69beff4037aadda808f886.png)
[ssrf-01] principle and utilization examples of server-side Request Forgery vulnerability
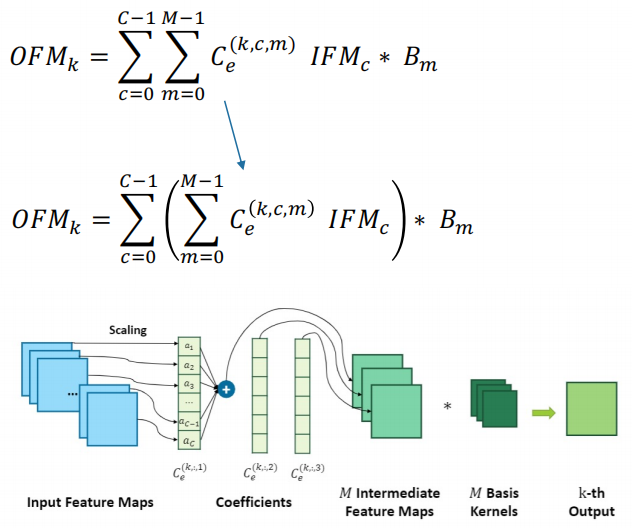
dried food! Accelerating sparse neural network through hardware and software co design

02.Go语言开发环境配置
Minecraft 1.18.1、1.18.2模组开发 22.狙击枪(Sniper Rifle)

Redis list
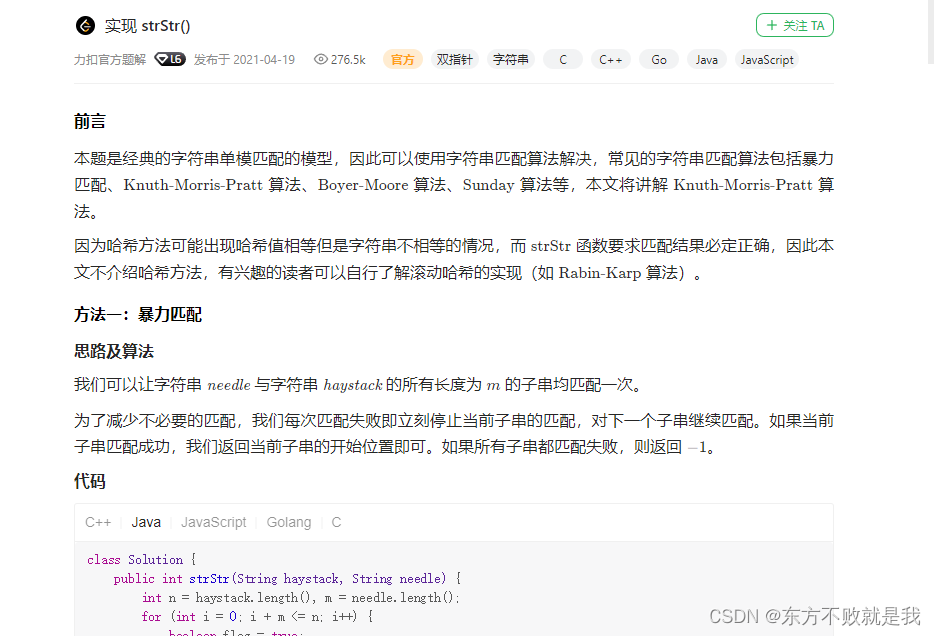
Leetcode3, implémenter strstr ()
随机推荐
Regular expressions: examples (1)
NiO related knowledge (II)
安装php-zbarcode扩展时报错,不知道有没有哪位大神帮我解决一下呀 php 环境用的7.3
Redis string type
Computer graduation design PHP enterprise staff training management system
RDD creation method of spark
Gbase 8C database upgrade error
数据工程系列精讲(第四讲): Data-centric AI 之样本工程
The ECU of 21 Audi q5l 45tfsi brushes is upgraded to master special adjustment, and the horsepower is safely and stably increased to 305 horsepower
dried food! Accelerating sparse neural network through hardware and software co design
2022年PMP项目管理考试敏捷知识点(8)
Genius storage uses documents, a browser caching tool
Prepare for the autumn face-to-face test questions
Executing two identical SQL statements in the same sqlsession will result in different total numbers
genius-storage使用文档,一个浏览器缓存工具
NLP fourth paradigm: overview of prompt [pre train, prompt, predict] [Liu Pengfei]
Minecraft 1.18.1、1.18.2模组开发 22.狙击枪(Sniper Rifle)
[flask] official tutorial -part3: blog blueprint, project installability
0211 embedded C language learning
同一个 SqlSession 中执行两条一模一样的SQL语句查询得到的 total 数量不一样