当前位置：网站首页>二叉树的常见算法总结

二叉树的常见算法总结

2020-11-06 01:18:00 【ClawHub的博客】

节点定义

1
2
3
4
5
6
7
8
9
10
11
12
13
 
public static class BinaryNode<T> {
    T element;
    BinaryNode<T> left;
    BinaryNode<T> right;
    BinaryNode(T theElement) {
        this(theElement, null, null);
    }
    BinaryNode(T theElement, BinaryNode<T> lt, BinaryNode<T> rt) {
        element = theElement;
        left = lt;
        right = rt;
    }
}

二叉树节点包括元素值与左右子节点引用。

创建节点

1
2
3
4
5
6
7
 
BinaryNode g = new BinaryNode(7);
BinaryNode f = new BinaryNode(6);
BinaryNode e = new BinaryNode(5);
BinaryNode d = new BinaryNode(4);
BinaryNode c = new BinaryNode(3, f, g);
BinaryNode b = new BinaryNode(2, d, e);
BinaryNode a = new BinaryNode(1, b, c);

形如：
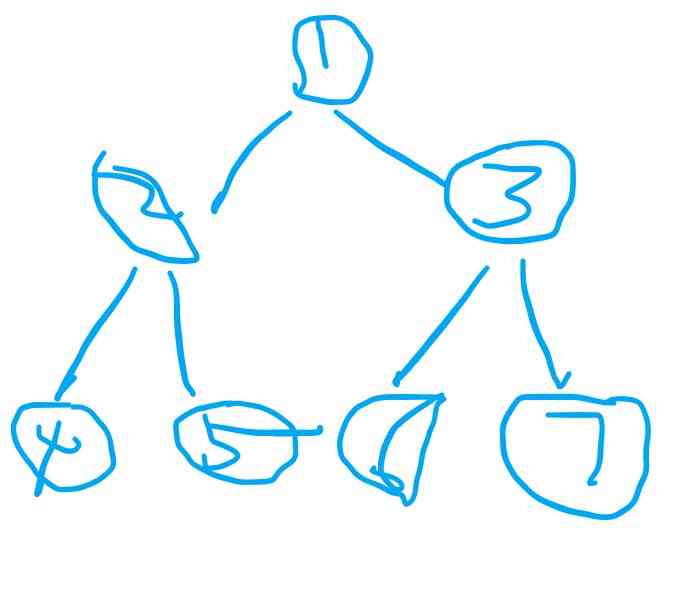
二叉树.jpg

1、前、中、后序遍历

二叉树的前、中、后序遍历中的前、中、后指的是根节点；
前序：先输出根节点，之后左右节点。
中序：先左，之后输出根节点，再右。
后序：先左右，再输出根节点。

1
2
3
 
public static void visit(BinaryNode p) {
    System.out.print(p.element + " ");
}

1.1、前序遍历

1
2
 
根->左->右
1 2 4 5 3 6 7
1.1.1、递归实现
1
2
3
4
5
6
 
 public static void recursivePreOrder(BinaryNode p) {
    if (p == null) return;
    visit(p);
    recursivePreOrder(p.left);
    recursivePreOrder(p.right);
}

如果节点为null,直接返回；
先打印出根节点，之后递归左子树，再递归右子树。
正好符合：先根，再左右。

1.1.2、非递归实现
1
2
3
4
5
6
7
8
9
10
11
 
public static void iterativePreOrder(BinaryNode p) {
    if (p == null) return;
    Stack<BinaryNode> stack = new Stack<>();
    stack.push(p);
    while (!stack.empty()) {
        p = stack.pop();
        visit(p);
        if (p.right != null) stack.push(p.right);
        if (p.left != null) stack.push(p.left);
    }
}

充分利用了栈的思路，先进后出。
当节点非空时，将节点入栈，迭代栈内元素，弹出栈顶元素，当前为根元素，之后将其右左子节点分别压栈。这样子节点出栈的顺序就是先左再右。

1.2、中序遍历

1
2
 
左->根->右
4 2 5 1 6 3 7
1.2.1、递归实现
1
2
3
4
5
6
 
public static void recursiveInOrder(BinaryNode p) {
    if (p == null) return;
    recursiveInOrder(p.left);
    visit(p);
    recursiveInOrder(p.right);
}
1.2.2、非递归实现
1
2
3
4
5
6
7
8
9
10
11
12
13
 
public static void iterativeInOrder(BinaryNode p) {
    if (p == null) return;
    Stack<BinaryNode> stack = new Stack<>();
    while (!stack.empty() || p != null) {
        while (p != null) {
            stack.push(p);
            p = p.left;
        }
        p = stack.pop();
        visit(p);
        p = p.right;
    }
}

1.3、后序遍历

1
2
 
左->右->根
4 5 2 6 7 3 1
1.3.1、递归实现
1
2
3
4
5
6
 
public static void recursivePostOrder(BinaryNode p) {
    if (p == null) return;
    recursivePostOrder(p.left);
    recursivePostOrder(p.right);
    visit(p);
}
1.3.2、非递归实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
 
public static void iterativePostOrder(BinaryNode p) {
    if (p == null) return;
    Stack<BinaryNode> stack = new Stack<>();
    Stack<BinaryNode> result = new Stack<>();
    while (!stack.empty() || p != null) {
        while (p != null) {
            stack.push(p);
            result.push(p);
            p = p.right;
        }
        if (!stack.empty()) p = stack.pop().left;
    }
    while (!result.empty()) {
        p = result.pop();
        visit(p);
    }
}

2、BFS与DFS

2.1、BFS广度优先搜索

1
 
1234567

广度优先遍历就是按层读取节点元素，需要借助队列的数据结构。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
 
public static void levelOrderTraversal(BinaryNode node) {
    if (node == null) {
        System.out.print("empty tree");
        return;
    }
    LinkedList<BinaryNode> queue = new LinkedList<>();
    queue.add(node);
    while (!queue.isEmpty()) {
        BinaryNode binaryNode = queue.pollFirst();
        System.out.print(binaryNode.element + "  ");
        if (binaryNode.left != null) {
            queue.add(binaryNode.left);
        }
        if (binaryNode.right != null) {
            queue.add(binaryNode.right);
        }
    }
}

2.2、DFS深度优先搜索

1
 
1245367

从根节点出发，选择一条分支读取所有的元素，需要借助栈的数据结构。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
 
public static void depthTraversal(BinaryNode node) {
    if (node == null) {
        System.out.print("empty tree");
        return;
    }
    LinkedList<BinaryNode> stack = new LinkedList<>();
    stack.push(node);
    while (!stack.isEmpty()) {
        BinaryNode binaryNode = stack.pop();
        System.out.print(binaryNode.element);
        if (binaryNode.right != null) {
            stack.push(binaryNode.right);
        }
        if (binaryNode.left != null) {
            stack.push(binaryNode.left);
        }
    }
}

3、二叉树的深度

104. 二叉树的最大深度

3.1、递归

1
2
3
4
5
6
7
8
9
10
 
private static int calcDepth(BinaryNode node) {
    if (node == null) return 0;
    int ld = calcDepth(node.left);
    int rd = calcDepth(node.right);
    if (ld > rd) {
        return ld + 1;
    } else {
        return rd + 1;
    }
}

3.2、深度优先

maxDepth与每个分支的长度做比较更新，最终获取最深的分支长度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
 
public static int maxDepthDFS(BinaryNode node) {
    if (node == null) return 0;
    LinkedList<BinaryNode> stack = new LinkedList<>();
    LinkedList<Integer> value = new LinkedList<>();
    stack.push(node);
    value.push(1);
    int maxDepth = 0;
    while (!stack.isEmpty()) {
        BinaryNode binaryNode = stack.pop();
        int temp = value.pop();
        maxDepth = Math.max(temp, maxDepth);
        if (binaryNode.right != null) {
            stack.push(binaryNode.right);
            value.push(temp + 1);
        }
        if (binaryNode.left != null) {
            stack.push(binaryNode.left);
            value.push(temp + 1);
        }
    }
    return maxDepth;
}

3.3、广度优先

按层搜索，每进入一层，深度+1.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
 
public static int maxDepthBFS(BinaryNode node) {
    if (node == null) return 0;
    LinkedList<BinaryNode> queue = new LinkedList<>();
    queue.add(node);
    int maxDepth = 0;
    while (!queue.isEmpty()) {
        maxDepth++;
        BinaryNode binaryNode = queue.pollFirst();
        if (binaryNode.left != null) {
            queue.add(binaryNode.left);
        }
        if (binaryNode.right != null) {
            queue.add(binaryNode.right);
        }
    }
    return maxDepth;
}

4、二叉树镜像

通过深度或者广度遍历，将节点的左右子树交换。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
 
public static void mirror(BinaryNode root) {
    if (root == null) return;
    LinkedList<BinaryNode> stack = new LinkedList<>();
    stack.push(root);
    while (!stack.isEmpty()) {
        BinaryNode node = stack.pop();
        BinaryNode temp = node.left;
        node.left = node.right;
        node.right = temp;
        if (node.right != null) {
            stack.push(node.right);
        }
        if (node.left != null) {
            stack.push(node.left);
        }
    }
}

5、对称二叉树

101. 对称二叉树
这道题就是二叉树镜像的变种，如果两个二叉树对称，则：

  1. 两个根节点具有相同的值
  2. 每个树的左子树，都与另一个树的右子树相同
    递归实现： 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    		 
    public boolean isSymmetric(BinaryNode root) {
        return isMirror(root, root);
    }

    public boolean isMirror(BinaryNode t1, BinaryNode t2) {
        if (t1 == null && t2 == null) return true;
        if (t1 == null || t2 == null) return false;
        return (t1.val == t2.val)
            && isMirror(t1.right, t2.left)
            && isMirror(t1.left, t2.right);
    }
    迭代实现： 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    		 
    public boolean isSymmetric(BinaryNode root) {
        LinkedList<BinaryNode> q = new LinkedList<>();
        q.add(root);
        q.add(root);
        while (!q.isEmpty()) {
            BinaryNode t1 = q.poll();
            BinaryNode t2 = q.poll();
            if (t1 == null && t2 == null) continue;
            if (t1 == null || t2 == null) return false;
            if (t1.val != t2.val) return false;
            q.add(t1.left);
            q.add(t2.right);
            q.add(t1.right);
            q.add(t2.left);
        }
        return true;
    }

总结

二叉树的各种题目的算法在第一意识里会想到递归，但是递归深度过大时会出现栈溢出，所以相应的会使用迭代来实现，相应的也就引入队列或者栈的数据结构。
感觉最重要的算法就是DFS与BFS，其中DFS深度优先搜索使用栈的先进后出特性，而BFS广度优先搜索则使用队列的先进先出特性。

tencent.jpg

版权声明
本文为[ClawHub的博客]所创，转载请带上原文链接，感谢
https://clawhub.club/posts/2020/01/02/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84%E4%B8%8E%E7%AE%97%E6%B3%95/%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E5%B8%B8%E8%A7%81%E7%AE%97%E6%B3%95%E6%80%BB%E7%BB%93/

边栏推荐

猜你喜欢

随机推荐