一万字彻底学会堆和二叉树

堆

一、堆的基本概念

堆（heap）是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。

两个性质：

1️⃣堆中某个结点的值总是不大于或不小于其父结点的值；
2️⃣堆总是一棵完全二叉树。
所以堆要么是大堆要么是小堆

1.1完全二叉树

一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。

---

二、大堆和小堆

根据堆的两个性质可以分为大堆和小堆
大堆（父亲大于孩子）：

小堆（父亲小于孩子）：

---

三、堆的公式

假设父亲的下标是parent
leftchild = 2 * parent + 1；
rightchild = leftchild + 1；
假设孩子的下标是child（不管左右）
parent = （child - 1) / 2.

---

四、向下调整算法

现在我们要调小堆

前提条件：左子树和右子树都是小堆，而整棵树不是小堆

用图来演示过程：

void Swap(int* a, int* b)
{
    
	int tmp = *a;
	*a = *b;
	*b = tmp;
}



//向下调整
//小堆
void AdjustDown(int a[], int n, int parent)
{
    
	int child = 2 * parent + 1;
	while (child < n)
	{
    
		if (child + 1 < n && a[child] > a[child + 1])
		{
    
			child++;
		}
		if (a[child] < a[parent])
		{
    
			Swap(&a[child], &a[parent]);
			parent = child;
			child = 2 * parent + 1;
		}
		else
		{
    
			break;
		}
	}
}


int main()
{
    
	int a[] = {
     27, 15, 19, 18, 28, 34, 65, 49, 25, 37 };
	int sz = sizeof(a) / sizeof(a[0]);
	AdjustDown(a, sz, 0);
	return 0;
}

如果要建大堆，就把两个大于小于号逆置

---

五、建堆

上面的向下调整算法必须要满足左子树和右子树都是小堆，但是如果不满足这个条件就需要建堆

如图右子树就不满足小堆
从下向上建堆：

从倒数第一个非叶子节点（28），从后往前，依次向下调整。
建堆的时间复杂度为O（N）

28处节点求法（n个数字）：
（n - 1 - 1）/ 2

//建堆
	for (int i = (sz - 1 - 1) / 2; i >= 0; i--)
	{
    
		AdjustDown(a, sz, i);
	}

---

六、堆排序(易错)️️

排升序建大堆，排降序建小堆
如果反过来时间复杂度就为O(N^2)，而且父子关系全乱了
排降序思路：

选小的放数组后面，依次选次小的

方法：

建小堆，交换收尾元素，不把尾元素看成堆里面的，再向下调整(其他都是小堆)，就能选出次小的……

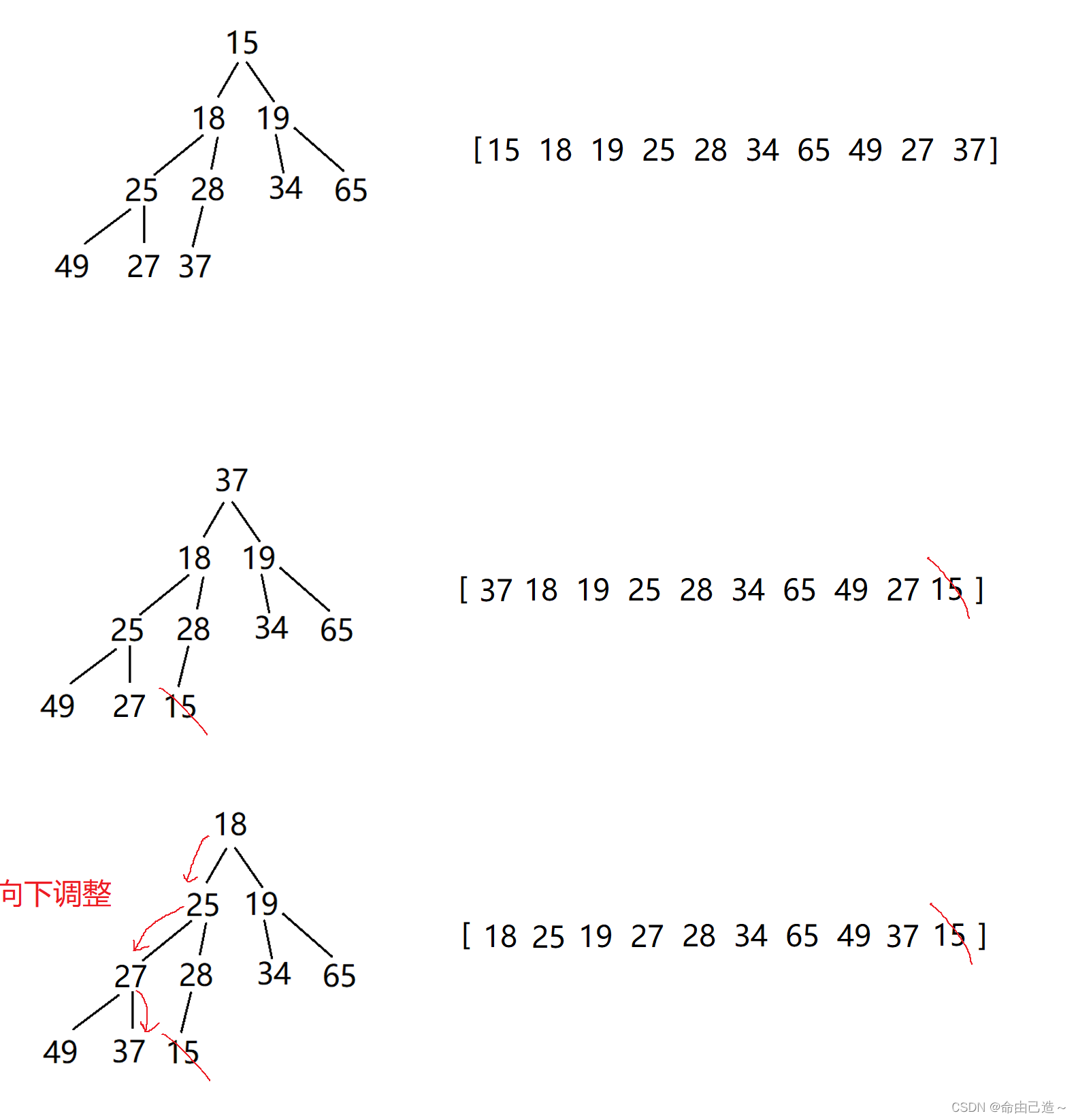
依次把数组元素向前调整，调完以后都是小堆。
这样时间复杂度为O(N * logN)，（建堆 * 向下调整）

void HeapSort(int a[], int n)
{
    
	//建小堆（降序）
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
    
		AdjustDown(a, n, i);
	}

	int end = n - 1;
	while (end)
	{
    
		Swap(&a[0], a[end]);
		AdjustDown(a, end, 0);
		end--;
	}
}

---

七、堆的接口实现

接口预览：

堆的结构

typedef int HPDataType;
struct Heap
{
    
	HPDataType* a;
	int size;
	int capacity;
};

typedef struct Heap HP;

7.1堆的初始化

void HeapInit(HP* php, HPDataType* a, int n)
{
    
	assert(php);
	php->a = (HPDataType*)malloc(sizeof(HPDataType) * n);
	if (php->a == NULL)
	{
    
		printf("malloc fail\n");
		exit(-1);
	}

	memcpy(php->a, a, n * sizeof(HPDataType));
	php->size = php->capacity = n;
	//建堆
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
    
		AdjustDown(php->a, php->size, i);
	}
}

7.2堆的销毁

void HeapDestroy(HP* php)
{
    
	assert(php);
	free(php->a);
	php->a = NULL;
	php->size = 0;
	php->capacity = 0;
}

7.3堆的插入

插入的时候注意判断是否满

void HeapPush(HP* php, HPDataType x)
{
    
	assert(php);
	if (php->size == php->capacity)
	{
    
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * php->capacity * 2);
		if (tmp == NULL)
		{
    
			printf("realloc fail\n");
			exit(-1);
		}
		php->a = tmp;
		php->capacity *= 2;
	}
	php->a[php->size] = x;
	php->size++;
	//向上调整
	AdjustUp(php->a, php->size - 1);
}

插入完后要调整为小堆（或大堆），采取向上调整算法

void AdjustUp(int* a, int child)
{
    
	int parent = (child - 1) / 2;
	while (child)
	{
    
		if (a[parent] > a[child])
		{
    
			Swap(&a[parent], &a[child]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
    
			break;
		}
	}
}

7.4堆的删除

删除首先把首尾元素交换，删除尾，再把首元素向下调整

void HeapPop(HP* php)
{
    
	assert(php);
	assert(php->size > 0);
	Swap(&php->a[0], &php->a[php->size - 1]);
	php->size--;
	AdjustDown(php->a, php->size, 0);
}

7.5返回堆顶元素

HPDataType HeapTop(HP* php)
{
    
	assert(php);
	assert(php->size > 0);
	return php->a[0];
}

7.6堆的大小

int HeapSize(HP* php)
{
    
	assert(php);
	return php->size;
}

7.7判断是否为空

bool HeapEmpty(HP* php)
{
    
	assert(php);
	return php->size == 0;
}

7.8打印堆

打印堆用条件控制形状

void HeapPrint(HP* php)
{
    
	assert(php);
	int row = 0;
	for (row = 1; row < php->size; row++)
	{
    
		if ((int)(pow(2, row) - 1) / php->size != 0)
		{
    
			break;
		}
	}
	int col = (int)pow(2, row - 1);
	int i = 0;
	int k = 0;
	for (i = 0; i < row; i++)
	{
    
		int j = 0;
		//打印空格
		for (j = 0; j < (col / 2) - i - 1; j++)
		{
    
			printf(" ");
		}
		for (j = 0; j < (int)pow(2, i); j++)
		{
    
			if (k >= php->size)
			{
    
				break;
			}
			printf("%d ", php->a[k++]);
		}
		printf("\n");
	}
}

效果图：

---

八、TopK问题️️

直接建堆用堆排序就可以做， 但是如果数据特别多，就会malloc非常多的节点，会出现问题。
所以我们可以只选前k个数建大堆，拿后边的所有数比较，如果堆顶元素大于后边的数，就让堆顶为这个数，再向下调整为大堆。最后的堆就是最小的k个数

/** * Note: The returned array must be malloced, assume caller calls free(). */


void Swap(int* a, int* b)
{
    
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

//大堆

void AdjustDown(int* a, int n, int parent)
{
    
    int child = 2 * parent + 1;
    while(child < n)
    {
    
        if(child + 1 < n && a[child] < a[child + 1])
        {
    
            child++;
        }
        if(a[parent] < a[child])
        {
    
            Swap(&a[parent], &a[child]);
            parent = child;
            child = 2 * parent + 1;
        }
        else
        {
    
            break;
        }
    }
}



int* getLeastNumbers(int* arr, int arrSize, int k, int* returnSize){
    
    if(k == 0)
    {
    
        *returnSize = 0;
        return NULL;
    }
    //取数前k个数
    int* a = (int*)malloc(sizeof(int) * k);
    for(int i = 0; i < k; i++)
    {
    
        a[i] = arr[i];
    }
    //建大堆
    for(int i = (k - 1 - 1) / 2; i >= 0; i--)
    {
    
        AdjustDown(a, k, i);
    }

    for(int i = k; i < arrSize; i++)
    {
    
        if(a[0] > arr[i])
        {
    
            a[0] = arr[i];
            AdjustDown(a, k, 0);
        }
    }
    *returnSize = k;
    return a;
}

---

---

二叉树

一、四种遍历顺序

1.1前序遍历

根→左→右
A→B→C→NULL→NULL→D→NULL→NULL→E→NULL→F→NULL→NULL

1.2中序遍历

左→根→右
NULL→C→NULL→B→NULL→D→NULL→A→NULL→E→NULL→F→NULL

1.3后序遍历

左→右→根
NULL→NULL→C→NULL→NULL→D→B→NULL→NULL→NULL→F→E→A

1.4层序遍历

一层一层走
A→B→E→C→D→F

---

二、二叉树的接口实现

2.1前序遍历

void PreOrder(BTNode* root)
{
    
	if (root == NULL)
	{
    
		printf("NULL ");
		return;
	}
	printf("%c ", root->val);
	PreOrder(root->left);
	PreOrder(root->right);
}

2.2中序遍历

void InOrder(BTNode* root)
{
    
	if (root == NULL)
	{
    
		printf("NULL ");
		return;
	}
	InOrder(root->left);
	printf("%c ", root->val);	
	InOrder(root->right);
}

2.3后序遍历

void PostOrder(BTNode* root)
{
    
	if (root == NULL)
	{
    
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%c ", root->val);
}

2.4求节点个数

int TreeSize(BTNode* root)
{
    
	if (root == NULL)
	{
    
		return 0;
	}
	return TreeSize(root->left) + TreeSize(root->right) + 1;
}

2.5求叶子节点个数

int TreeLeafSize(BTNode* root)
{
    
	if (root == NULL)
	{
    
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
    
		return 1;
	}
	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

2.6求第K层节点️️

求当前树的第K层的节点可以看成求（从第二层看）第K-1层的节点个数……求（从第K层看）第1层节点个数

int TreeLevelSize(BTNode* root, int k)
{
    
	if (root == NULL)
	{
    
		return 0;
	}
	if (k == 1)
	{
    
		return 1;
	}
	return TreeLevelSize(root->left, k - 1) + TreeLevelSize(root->right, k - 1);
}

2.7寻找目标节点️️

BTNode* TreeFind(BTNode* root, BTDataType x)
{
    
	if (root == NULL)
	{
    
		return NULL;
	}
	if (root->val == x)
	{
    
		return root;
	}
	BTNode* left = TreeFind(root->left, x);
	if (left)
	{
    
		return left;
	}
	BTNode* right = TreeFind(root->right, x);
	if (right)
	{
    
		return right;
	}
	return NULL;
}

2.8二叉树的销毁️️

后序遍历销毁节点：先销毁左树再销毁右树再销毁自己

2.8.1一级指针

void TreeDestroy(BTNode* root)
{
    
	if (root == NULL)
	{
    
		return;
	}
	TreeDestroy(root->left);
	TreeDestroy(root->right);
	free(root);
}

A = NULL;
如果用一级指针就要在调用销毁函数后边把指针置空。

2.8.2二级指针

void TreeDestroy(BTNode** pproot)
{
    
	if (*pproot == NULL)
	{
    
		return;
	}
	TreeDestroy(&(*pproot)->left);
	TreeDestroy(&(*pproot)->right);
	free(*pproot);
	*pproot = NULL;
}

三、深度优先广度优先遍历️️

3.1深度优先遍历

就是从图中一个未访问的顶点开始，沿着一条路一直走到底，然后从这条路尽头的节点回退到上一个节点，再从另一条路开始走到底…，不断递归重复此过程，直到所有的顶点都遍历完成，它的特点是不撞南墙不回头，先走完一条路，再换一条路继续走。

二叉树的前中后序遍历就是深度优先遍历

3.2广度优先遍历

广度优先遍历，指的是从图的一个未遍历的节点出发，先遍历这个节点的相邻节点，再依次遍历每个相邻节点的相邻节点。

二叉树的层序遍历就是广度优先遍历

3.3层序遍历的实现

首先确定用队列实现

1.先把根入队列

2.出队头数据，带入下一层数据

先引入写好的队列：一万字彻底学会栈和队列

void TreeLevelOrder(BTNode* root)
{
    
	Queue q;
	QueueInit(&q);
	if (root)
	{
    
		QueuePush(&q, root);
	}
	while (!QueueEmpty(&q))
	{
    
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%c ", front->data);
		if (front->left)
		{
    
			QueuePush(&q, front->left);
		}
		if (front->right)
		{
    
			QueuePush(&q, front->right);
		}
	}


	QueueDestroy(&q);
}

3.4判断是否为完全二叉树

用两个二叉树来总结规律：

可以看出完全二叉树层序遍历只要出现NULL，后边的都为NULL；
不是完全二叉树的NULL后边会有不为NULL的节点

bool BinaryTreeComplete(BTNode* root)
{
    
	Queue q;
	QueueInit(&q);
	if (root)
	{
    
		QueuePush(&q, root);
	}
	while (!QueueEmpty(&q))
	{
    
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front == NULL)
		{
    
			break;
		}
		else
		{
    
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
	}

	while (!QueueEmpty(&q))
	{
    
		BTNode* cur = QueueFront(&q);
		QueuePop(&q);
		if (cur)
		{
    
			QueueDestroy(&q);
			return false;
		}
	}
	QueueDestroy(&q);
	return true;
}