当前位置:网站首页>统计学习方法——感知机
统计学习方法——感知机
2022-07-07 13:53:00 【_春天_】
感知机是机器学习的最基本模型之一,是神经网络和支持向量机的基础。
感知机的关键词
- 二分类
- 判别模型、线性模型
- 数据集线性可分时,有无穷多个解
- 无法解决XOR问题
感知机的原理
感知机是根据数据实例的特征向量x对其进行二类分类的线形分类模型,输出为+1或-1。感知机的函数为:
f ( x ) = s i g n ( w ⋅ x + b ) f(x)=sign(w·x+b) f(x)=sign(w⋅x+b)
其中 w w w是权值, b b b是偏置, w ⋅ x w·x w⋅x是 w w w和 x x x的内积, s i g n sign sign是符号函数,即,
s i g n ( x ) = { + 1 x ≥ 0 − 1 x < 0 sign(x) = \begin{cases} +1 & x\ge 0\\ -1 & x <0 \end{cases} sign(x)={ +1−1x≥0x<0当wx+b大于0时,根据sign函数,输出为1,对应正类;当wx+b小于0,输出为-1,对应负类。感知机的几何解释:线性方程 w ⋅ x + b = 0 w·x+b=0 w⋅x+b=0 对应于特征空间中一个超平面 S S S,这个超平面将特征空间划分为两个部分,位于两部分的点(特征向量)分别被分为正、负两类。超平面 S S S也被称为分离超平面。
一个线性方程将特征空间分成两部分。在二维特征空间内,wx+b=0即为一条之间,将平面分为两部分,直线上方的点带入wx+b计算值大于0,为正类,对应y值为+1,直线下方的点小于0,为负类,对应y值为-1。感知机学习的策略是极小化损失函 数:
m i n w , b L ( w , b ) = − ∑ y i ( w ⋅ x i + b ) , x i ∈ M min_w, _bL(w,b)=-\sum y_i(w·x_i+b), x_i \in M minw,bL(w,b)=−∑yi(w⋅xi+b),xi∈M
损失函数对应误分类点到分离超平面的总距离。该处的损失函数关注的是误分类点,而不是所有点。损失函数最小为零,即所有的点都分类正确。因此也导致了有无穷多个解。感知机学习算法是基于随机梯度下降法的对损失函数的最优化算法。在原始形式中,首先选取一个超平面,然后用梯度下降法不断极小化目标函数,在这个过程中,一次随机选取一个误分类点使其梯度下降。
当训练数据集线性可分时[补充1],感知机学习算法是收敛的,但是存在无穷多个解,这些解既依赖于处值的选择,也依赖于迭代过程中误分类点的选择顺序。
如果想要得到唯一的超平面,就需要对分离超平面增加约束条件。可参考支持向量机
为什么不能解决异或(XOR)问题
异或问题为二进制运算中,值相同为0,不相同为1。
把异或问题映射到二维空间里,可表示为: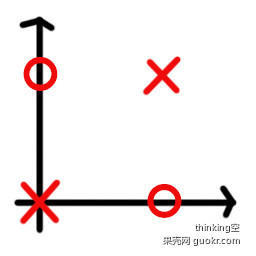
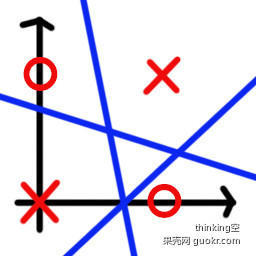
在这个二维空间下,我们找不到一条直线将其分成两类。也就是说无法通过感知机模型将X分到直线的一边,同时将O分到直线的另一边。所以感知机解决不了异或问题。
补充知识
- 补充1:数据集的线性可分性
给定一个数据集
T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x N , y N ) } T=\{(x_1, y_1), (x_2, y_2),…, (x_N, y_N)\} T={ (x1,y1),(x2,y2),…,(xN,yN)}
其中, x i ∈ X = R n x_i \in X = R^n xi∈X=Rn, y i ∈ Y = { + 1 , − 1 } y_i \in Y=\{+1,-1\} yi∈Y={ +1,−1}, i = 1 , 2 , … , N i=1,2,…,N i=1,2,…,N,如果存在某个超平面 S S S
w ⋅ x + b = 0 w·x+b=0 w⋅x+b=0能够将数据集的正实例点和负实例点完全正确地划分到超平面的两侧,即对所有 y i = + 1 y_i=+1 yi=+1的实例 i i i,有 w ⋅ x i + b > 0 w·x_i+b>0 w⋅xi+b>0,对所有 y i = − 1 y_i=-1 yi=−1的实例 i i i,有 w ⋅ x i + b < 0 w·x_i+b<0 w⋅xi+b<0,则称数据集 T T T为线性可分数据集(Linearly separable data set);否则,称数据集 T T T线形不可分。
推荐阅读:
边栏推荐
- nodejs package. JSON version number ^ and~
- 持续创作,还得靠它!
- UE4 exports the picture + text combination diagram through ucanvasrendertarget2d
- 2022第四届中国(济南)国际智慧养老产业展览会,山东老博会
- numpy--疫情数据分析案例
- 企业级日志分析系统ELK
- Unity drawing plug-in = = [support the update of the original atlas]
- 星瑞格数据库入围“2021年度福建省信息技术应用创新典型解决方案”
- Webcodecs parameter settings -avc1.42e01e meaning
- AE learning 01: AE complete project summary
猜你喜欢

Rongyun won the 2022 China Xinchuang digital office portal excellence product award!
AB package details in unity (super detail, features, packaging, loading, manager)

Three. JS introductory learning notes 11:three JS group composite object

LeetCode3_ Longest substring without duplicate characters

融云斩获 2022 中国信创数字化办公门户卓越产品奖!
Syntax of generator function (state machine)

Cocos uses custom material to display problems
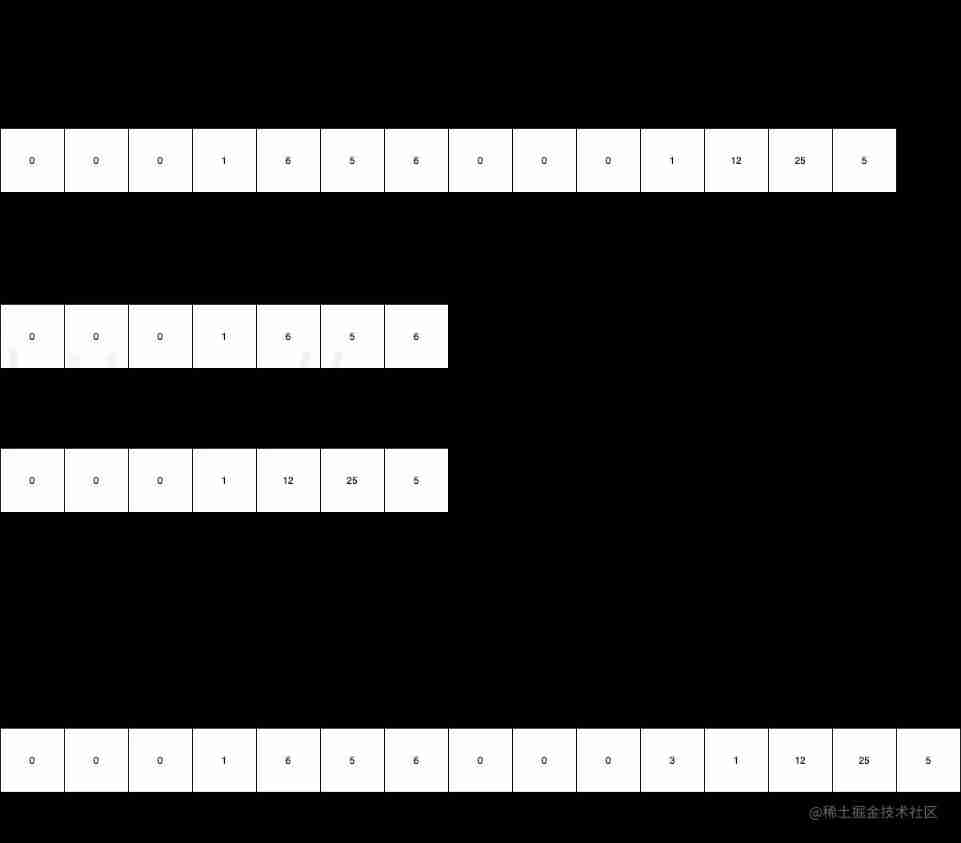
Annexb and avcc are two methods of data segmentation in decoding

Ue4/ue5 multi thread development attachment plug-in download address
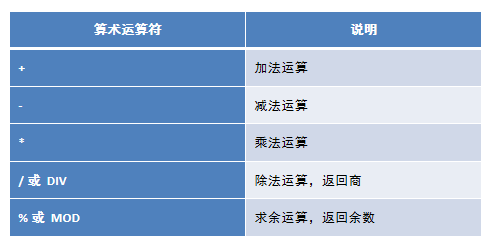
MySQL数据库基本操作-DQL-基本查询
随机推荐
Introduction to pyGame games
asyncio 概念和用法
【花雕体验】15 尝试搭建Beetle ESP32 C3之Arduino开发环境
Three. JS introductory learning notes 18: how to export JSON files with Blender
Unity3D_ Class fishing project, bullet rebound effect is achieved
Learn good-looking custom scroll bars in 1 minute
应用程序和matlab的通信方式
Shipping companies' AI products are mature, standardized and applied on a large scale. CIMC, the global leader in port and shipping AI / container AI, has built a benchmark for international shipping
Async and await
There are many ways to realize the pause function in JS
谈谈 SAP iRPA Studio 创建的本地项目的云端部署问题
C4D learning notes 2- animation - timeline and time function
持续创作,还得靠它!
A JS script can be directly put into the browser to perform operations
安科瑞电网智能化发展的必然趋势电力系统采用微机保护装置是
leetcode 241. Different Ways to Add Parentheses 为运算表达式设计优先级(中等)
Three. JS introductory learning notes 07: external model import -c4d to JSON file for web pages -fbx import
Vertex shader to slice shader procedure, varying variable
numpy---基础学习笔记
Three. JS introductory learning notes 13: animation learning