当前位置:网站首页>2016 CCPC Hangzhou Onsite
2016 CCPC Hangzhou Onsite
2022-07-07 07:09:00 【moyangxian】
2016 CCPC Hangzhou Onsite
A ArcSoft’s Office Rearrangement(贪心)
题意:将n个数分成k个相同的数,一次操作能将两个数合并或将一个数拆分成两个数。求最小操作数
题记:求出n个数的总和除k的值s,遍历数组,将x加上a[i](如果x不为0,即上次操作有剩余的数,要将a[i]加到x中答案要加一),用x去记录当前的数有多大,当x>s时将x拆分出s,直到x<s。要特判x==s的情况答案是不用加一的。
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e5+10;
int a[N];
int cas;
void solve(){
int n,k;
scanf("%lld%lld",&n,&k);
int sum=0;
for(int i=1;i<=n;i++){
scanf("%lld",&a[i]);
sum+=a[i];
}
if(sum%k){
printf("Case #%lld: -1\n",++cas);
return ;
}
int s=sum/k;
int x=0,ans=0;
for(int i=1;i<=n;i++){
if(x>0) ans++;
x+=a[i];
while(x>s){
x-=s;
ans++;
}
if(x==s) x-=s;
}
printf("Case #%lld: %lld\n",++cas,ans);
}
signed main(){
int T;
scanf("%lld",&T);
while(T--){
solve();
}
return 0;
}
B Bomb(Tarjan+缩点)
题意:有n个炸弹,每个炸弹有一个坐标、爆炸范围和引爆花费。求所有炸弹爆炸的最小花费。
题记:Tarjan求出所有强连通分量,然后缩点,求入度为0的点的最小花费即可。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1010;
const int INF=0x3f3f3f3f;
ll x[N],y[N],r[N],c[N];
ll ans;
int n,cas;
int cnt;
int low[N],num[N],dfn,du[N];
int scc[N],Stack[N],top;
vector<int>g[N];
ll w[N];
void dfs(int u){
Stack[top++]=u;
low[u]=num[u]=++dfn;
for(int i=0;i<g[u].size();i++){
int v=g[u][i];
if(!num[v]){
dfs(v);
low[u]=min(low[v],low[u]);
}
else if(!scc[v])
low[u]=min(low[u],num[v]);
}
if(low[u]==num[u]){
cnt++;
while(1){
int v=Stack[--top];
scc[v]=cnt;
if(u==v) break;
}
}
}
void tarjan(){
for(int i=1;i<=n;i++)
if(!num[i])
dfs(i);
}
void init(){
for(int i=1;i<=n;i++) g[i].clear();
cnt=top=dfn=0;
memset(scc,0,sizeof(scc));
memset(num,0,sizeof(num));
memset(low,0,sizeof(low));
memset(du,0,sizeof(du));
}
ll dis(ll x1,ll y1,ll x2,ll y2){
return (x1-x2)*(x1-x2)+(y1-y2)*(y1-y2);
}
void solve(){
scanf("%d",&n);
init();
for(int i=1;i<=n;i++)
scanf("%lld%lld%lld%lld",&x[i],&y[i],&r[i],&c[i]);
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(i==j) continue;
ll d=dis(x[i],y[i],x[j],y[j]);
if(d<=r[i]*r[i])
g[i].push_back(j);
}
}
/* for(int i=1;i<=n;i++){ for(int j=0;j<g[i].size();j++) cout<<g[i][j]<<" "; cout<<endl; } */
tarjan();
/* for(int i=1;i<=n;i++) cout<<scc[i]<<" "; cout<<endl; */
memset(w,INF,sizeof(w));
for(int i=1;i<=n;i++){
int x=scc[i];
w[x]=min(w[x],c[i]);
for(int j=0;j<g[i].size();j++){
int v=g[i][j];
int y=scc[g[i][j]];
if(x!=y) du[y]++;
}
}
/* for(int i=1;i<=cnt;i++) cout<<du[i]<<" "; cout<<endl; */
ll ans=0;
//cout<<cnt<<endl;
for(int i=1;i<=cnt;i++){
if(du[i]==0)
ans+=w[i];
}
printf("Case #%d: %lld\n",++cas,ans);
}
int main(){
int T;
scanf("%d",&T);
while(T--){
solve();
}
return 0;
}
C Car(贪心+卡精度)
题意:记录一辆车整数时刻路过的坐标,问车开到终点最少用时。
题记:由于速度是非降的,所以贪心的设最后一段路程的用时为一秒,速度为最后一段的路程。然后向前遍历会有两种情况:
1、路程<=速度,那么用时为一秒,速度变为当前路程。
2、路程>速度,那么时间等于路程/速度+1,速度等于路程/时间。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int INF=0x3f3f3f3f;
const int N=1e5+10;
const double eps=1e-8;
int cas;
int a[N];
void solve(){
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
a[0]=0;
if(n==1){
printf("Case #%d: 1\n",++cas);
return ;
}
double v=1.0*(a[n]-a[n-1]);
int ans=0;
for(int i=n-1;i>=0;i--){
double s=1.0*(a[i+1]-a[i]);
if(v>=s){
v=s;
ans++;
}
else{
int t=int((s-eps)/v)+1;
v=s/t;
ans+=t;
}
}
printf("Case #%d: %d\n",++cas,ans);
}
signed main(){
int T;
scanf("%d",&T);
while(T--){
solve();
}
return 0;
}
D Difference(思维+二分)
题意:求符合式子x=f(y,K)-y,y的数量。
题记:首先猜y最多只有10位,可以估算一下y是10位数的情况已经是极限了。所以将y分成A*1e5+B这种形式。那么题目要求的式子就变成了x=f(A,k)+f(B,k)-(A*1e5-B),我们提前算出1e5内f(B,k)-B所有的数,然后枚举A,在所有数中二分找符合条件的数即可。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5;
int f[N+10];
int a[N+10];
int n,k,cas;
int qpow(int a,int b){
int res=1;
while(b){
if(b&1) res=res*a;
a=a*a;
b>>=1;
}
return res;
}
int getnum(int x){
int res=0;
while(x){
int s=x%10;
res+=qpow(s,k);
x/=10;
}
return res;
}
void init(){
for(int i=0;i<=N;i++){
f[i]=getnum(i);
//cout<<i<<" "<<f[i]<<endl;
}
for(int i=0;i<=N;i++){
a[i]=f[i]-i;
//cout<<a[i]<<" "<<i<<endl;
}
sort(a,a+1+N);
}
void solve(){
cin>>n>>k;
init();
int ans=0;
for(int i=0;i<=N;i++){
int s=n-f[i]+i*N;
int p=lower_bound(a,a+1+N,s)-a;
while(p<=N&&a[p]==s){
//cout<<a[p]<<endl;
ans++;
p++;
}
}
if(n==0) ans--;
printf("Case #%lld: %lld\n",++cas,ans);
}
signed main(){
int T;
cin>>T;
while(T--){
solve();
}
return 0;
}
E Equation(dfs剪枝)
题意:给出1-9数的个数,求有多少种a+b=c的组合。
题记:打表可看出答案最多有36种,然后dfs这36种可能即可。
#include<bits/stdc++.h>
using namespace std;
const int N=10;
int a[N];
int ans,cas,cnt;
struct Node{
int x,y,z;
}s[100];
void f(){
for(int i=1;i<=9;i++){
for(int j=1;j<=9;j++){
//if(i+j<=9) ans++;
if(i+j>9) continue;
s[++cnt]={
i,j,i+j};
}
}
//cout<<cnt<<endl;
//36
}
void dfs(int p,int res){
if(p>cnt){
ans=max(ans,res);
return ;
}
if(cnt-p+res+1<=ans) return ;
int x=s[p].x;int y=s[p].y;int z=s[p].z;
if(a[x]&&a[y]&&a[z]){
a[x]--;a[y]--;a[z]--;
if(a[x]>=0&&a[y]>=0&&a[z]>=0)dfs(p+1,res+1);
//cout<<x<<" "<<y<<" "<<z<<endl;
a[x]++;a[y]++;a[z]++;
}
dfs(p+1,res);
}
void solve(){
for(int i=1;i<=9;i++)
scanf("%d",&a[i]);
ans=0;
dfs(1,0);
printf("Case #%d: %d\n",++cas,ans);
}
int main(){
f();
int T;
scanf("%d",&T);
while(T--){
solve();
}
return 0;
}
F Four Operations(贪心,模拟)
题意:给一串长为n的数字字符串,在字符串中加上’+’、’-’、’*’、’/’。使得答案最大。
题记:最后形成的式子是A+B-CD/E,很明显我们贪心得让A+B尽可能得大,CD/E尽可能小,C和D都只取一位,E取一位或者两位(例如:111991)。直接模拟一遍求最大值即可。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int INF=0x3f3f3f3f;
const int N=1e5+10;
ll a,b,c,d,e;
int cas;
string ss;
ll check(int p){
ll res=-INF;
d=ss[p]-'0';
p--;
c=ss[p]-'0';
p--;
ll s=0;
for(int i=1;i<=p;i++)
s=s*10+(ss[i]-'0');
s+=ss[0]-'0';
res=max(res,s);
s=0;
for(int i=0;i<p;i++)
s=s*10+(ss[i]-'0');
s+=ss[p]-'0';
res=max(res,s);
res=res-c*d/e;
return res;
}
void solve(){
cin>>ss;
ll ans=-INF;
int n=ss.size()-1;
e=ss[n]-'0';
ans=max(ans,check(n-1));
e=(ss[n-1]-'0')*10+(ss[n]-'0');
if(n>=5)ans=max(ans,check(n-2));
printf("Case #%d: %lld\n",++cas,ans);
}
signed main(){
int T;
scanf("%d",&T);
while(T--){
solve();
}
return 0;
}
K Kingdom of Obsession(素数距离,二分图匹配)
题意:x取s+1 - s+n,y取1 - n。求所有的x%y==0。
题记:首先一个素数只有mod1和它本身才会==0。所以只有区间内有两个或两个以上的素数就不符合条件。在1e9内两个素数之间的距离不超过600。所以当min(n,s)大于600时就不符合条件了。之后就对剩下的n个数做二分图匹配即可。
#include<bits/stdc++.h>
using namespace std;
const int N=610;
vector<int>g[N];
bool vis[N];
int match[N];
int n,s,cas;
void init(){
memset(match,0,sizeof(match));
for(int i=1;i<=n;i++)
g[i].clear();
}
bool dfs(int u){
for(int i=0;i<g[u].size();i++){
int v=g[u][i];
if(!vis[v]){
vis[v]=true;
if(!match[v]||dfs(match[v])){
match[v]=u;
return true;
}
}
}
return false;
}
void solve(){
scanf("%d%d",&n,&s);
if(n>s) swap(n,s);
if(n>600){
printf("Case #%d: No\n",++cas);
return ;
}
init();
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if((s+j)%i==0)
g[i].push_back(j);
int ans=0;
for(int i=1;i<=n;i++){
memset(vis,false,sizeof(vis));
if(dfs(i)) ans++;
}
if(ans==n)
printf("Case #%d: Yes\n",++cas);
else
printf("Case #%d: No\n",++cas);
}
int main(){
int T;
scanf("%d",&T);
while(T--){
solve();
}
return 0;
}
边栏推荐
- What is MD5
- 【无标题】
- flex弹性布局
- How to speed up video playback in browser
- Lesson 1: hardness of eggs
- 软件建模与分析
- JMeter JDBC batch references data as input parameters (the simplest method for the whole website)
- Difference between process and thread
- Information Security Experiment 4: implementation of IP packet monitoring program
- Database multi table Association query problem
猜你喜欢
Loxodonframework quick start
nlohmann json
JS逆向教程第一发
JMeter JDBC batch references data as input parameters (the simplest method for the whole website)
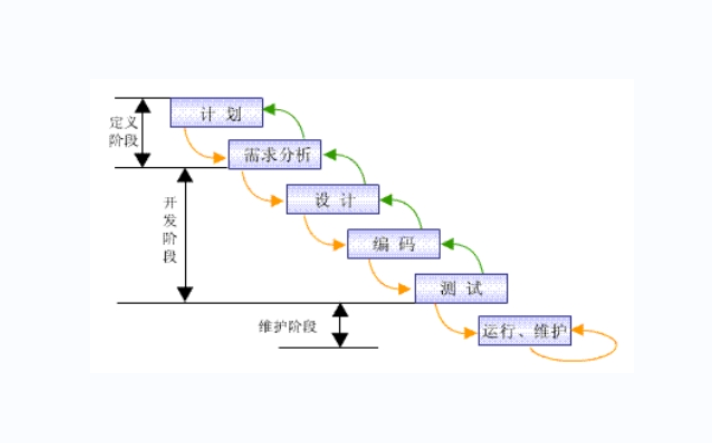
What development models did you know during the interview? Just read this one
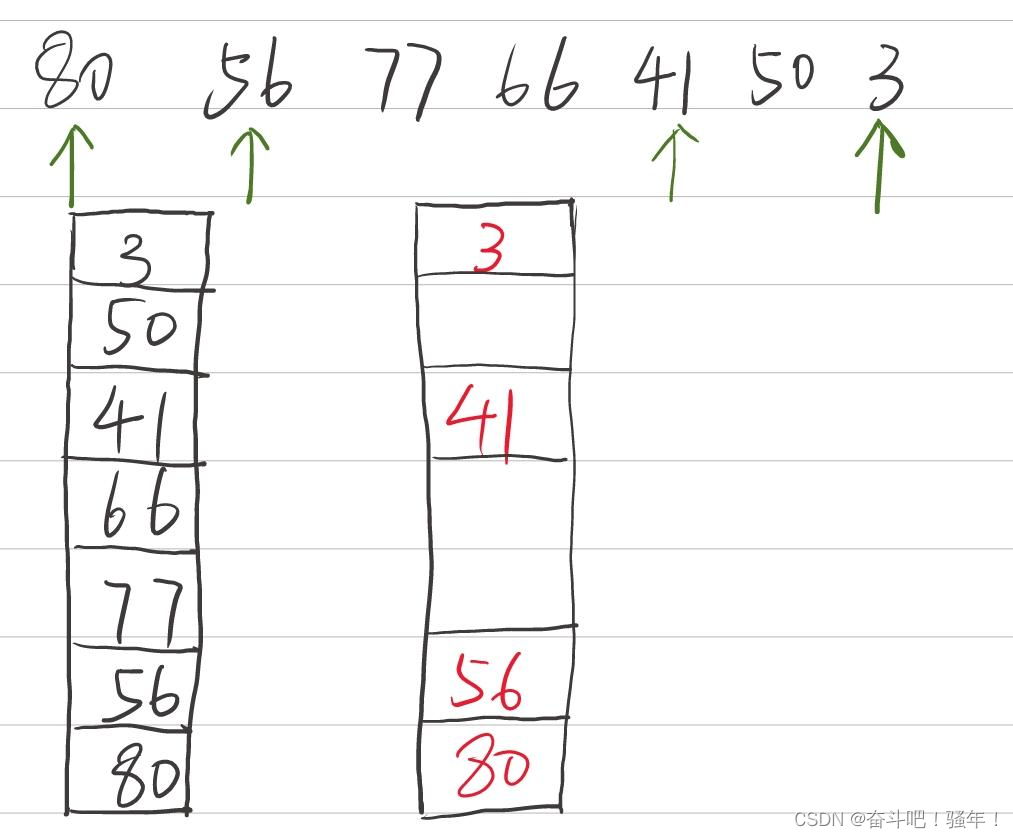
Lecture 1: stack containing min function
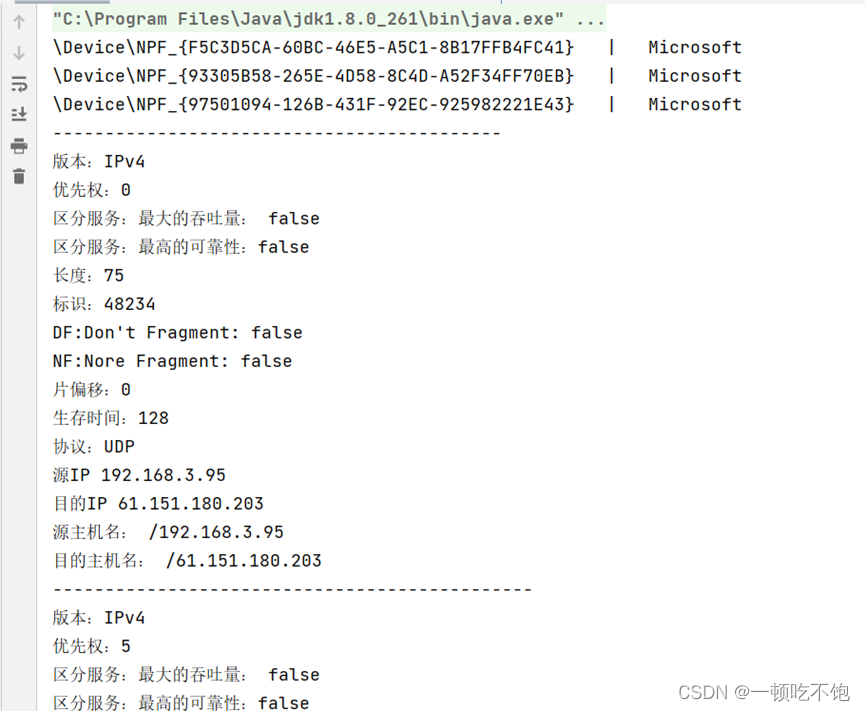
Information Security Experiment 4: implementation of IP packet monitoring program
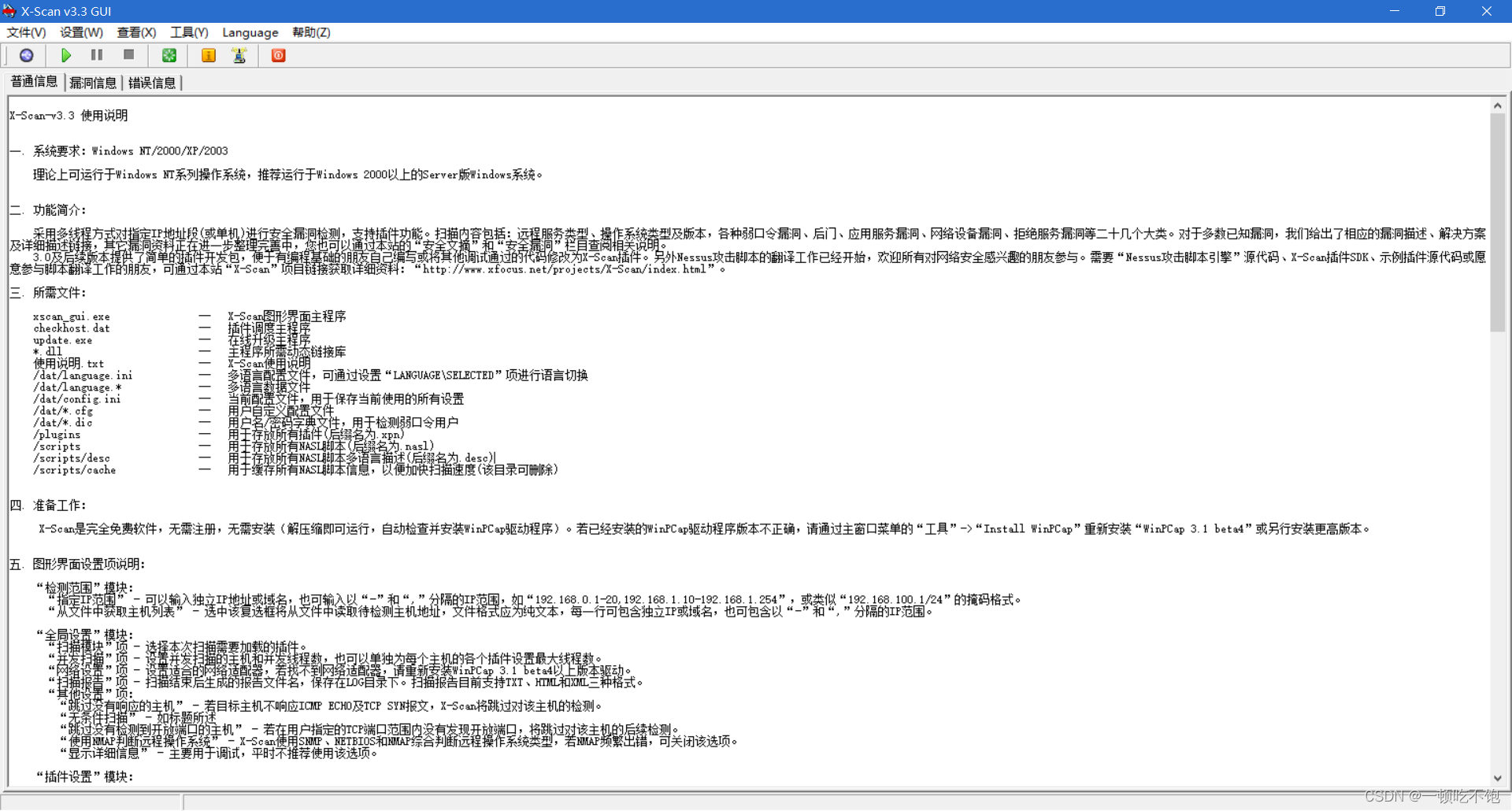
Information Security Experiment 2: using x-scanner scanning tool
其实特简单,教你轻松实现酷炫的数据可视化大屏
Binary tree high frequency question type
随机推荐
sql 里面使用中文字符判断有问题,哪位遇到过?比如value&lt;&gt;`无`
PLC信号处理系列之开关量信号防抖FB
MongoDB怎么实现创建删除数据库、创建删除表、数据增删改查
NATAPP内网穿透
信息安全实验一:DES加密算法的实现
根据热门面试题分析Android事件分发机制(二)---事件冲突分析处理
CMD startup software passes in parameters with spaces
信息安全实验二 :使用X-SCANNER扫描工具
2020浙江省赛
H5 web player easyplayer How does JS realize live video real-time recording?
Write VBA in Excel, connect to Oracle and query the contents in the database
Esp8266 uses TF card and reads and writes data (based on Arduino)
Can flycdc use SqlClient to specify mysqlbinlog ID to execute tasks
进程间的通信方式
La différence entre viewpager 2 et viewpager et la mise en œuvre de la rotation viewpager 2
flink. CDC sqlserver. 可以再次写入sqlserver中么 有连接器的 dem
How to become a senior digital IC Design Engineer (5-3) theory: ULP low power design technology (Part 2)
Add new item after the outbound delivery order of SAP mm sto document is created?
**Grafana installation**
如何成为一名高级数字 IC 设计工程师(5-2)理论篇:ULP 低功耗设计技术精讲(上)