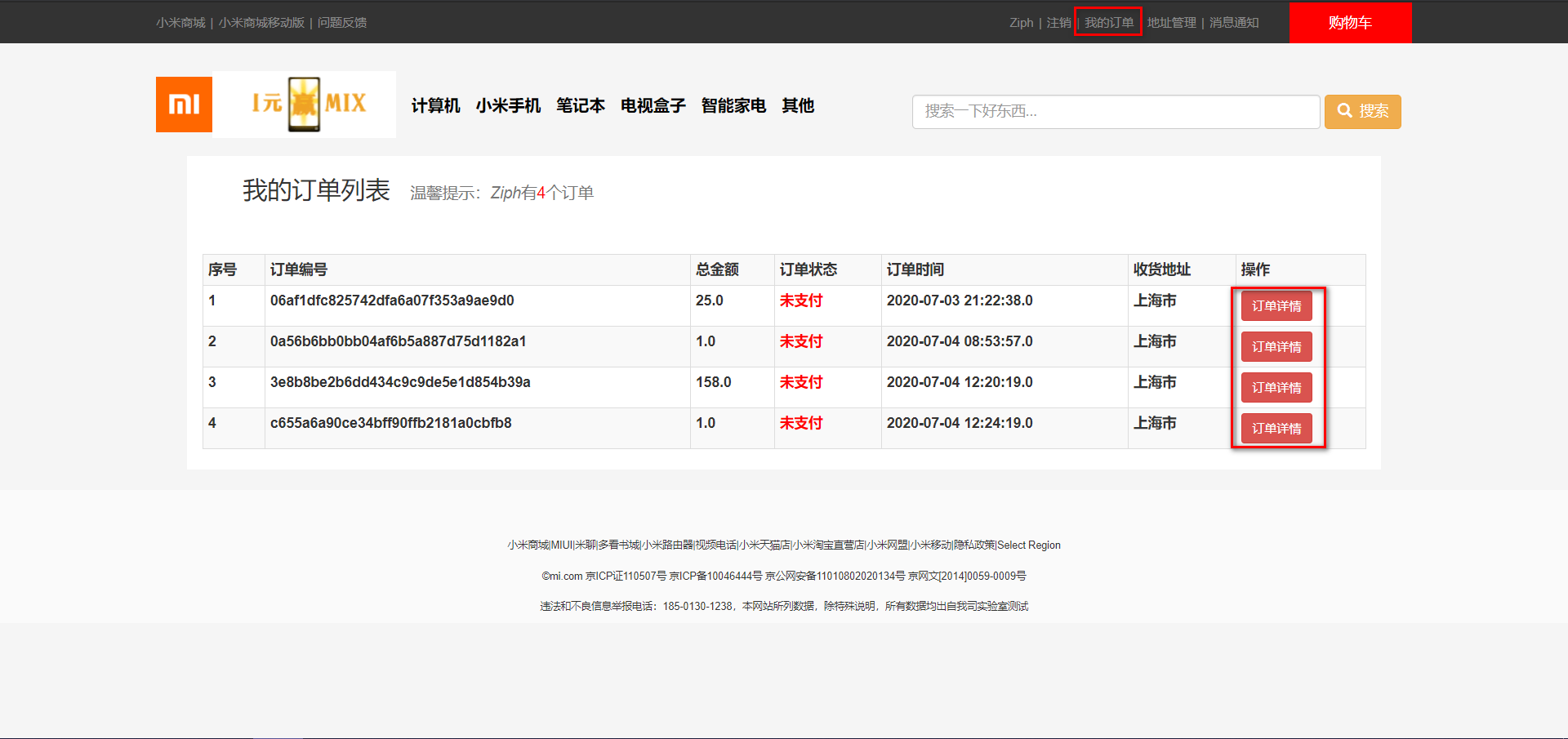
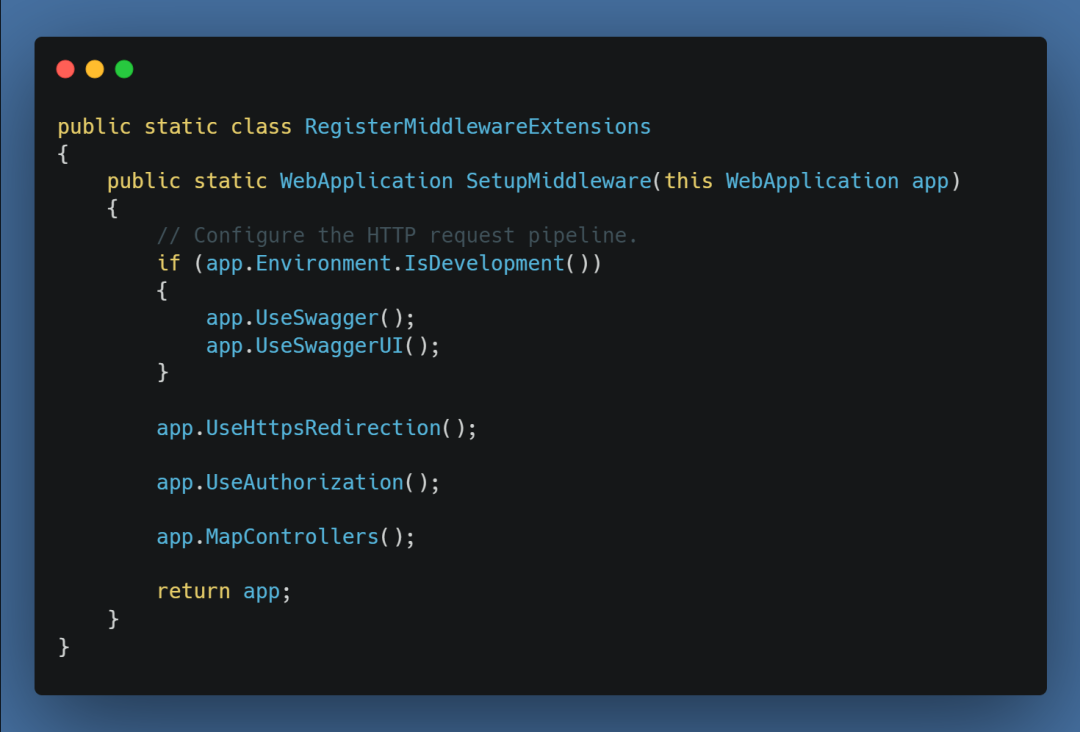
1. At least the general meaning of the coin problem ：
Yes n Grow coins , The face values are v1,v2......vn, The number is unlimited , Enter a non negative integer s, Choose coins to sum s, It is required to output the least coin combination .
We can analyze it like this ：
Define a name Min[s] An array of is used to represent the amount s The combination of the corresponding minimum coins , So for us , As long as it is found in the program Min[i] You can know the minimum coin combination by the size of .
At par value {1,5,10,25,50} For example , It's convenient to prepare for the race in the future .
Suppose we enter s yes 100, When all use 1coin When , Pictured ：( The painting is very clumsy , I'm sorry ）
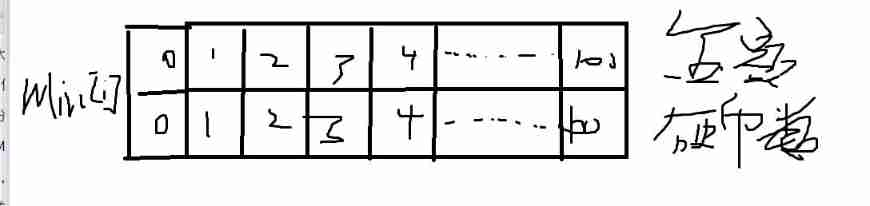
Then the first box refers to when the amount is 0 The number of coins needed is 0, The amount is 1 When Min[1]=Min[1-1]+1, And so on , Of course , This is a coin with a face value of 1 When .
When we add face value 5, It's like this ：
We can see , here we are 5 When , There are two choices —— One is 5 individual 1 Yuan coins , The other is the direct one 5 Yuan coins , It's understandable ：
Min[5]=min(Min[5],Min[5-5]+1), In this way, the number of coins can be minimized .
We also have coins of other denominations , Of course, it should also be introduced one by one .
So , We are dp Lieutenant general Min[i] This kind of data recording the optimal solution of the problem is called “ state ”, from Min【i-1】,Min【i-5】 This formula is called state transition , In question , We can clearly see that dynamic planning often uses the state in front of the problem , That is to use the relevance of subproblems to solve problems , This is a dp One of the characteristics of .
The solution of this problem is as follows ：
1 #include<bits/stdc++.h> 2 using namespace std; 3 int Min[251];// The minimum number of coins corresponding to each amount 4 int coin[5]={1,5,10,25,50};//5 Kind of money 5 int Min_path[251]={0}; 6 void ans() 7 { 8 for(register int k=0;k<251;k++) 9 Min[k]=INT_MAX;// Define the initial value as infinity 10 Min[0]=0; 11 for(register int j=0;j<5;j++) 12 13 for(register int i=coin[j];i<251;i++) 14 { 15 Min_path[i]=coin[j]; 16 Min[i]=min(Min[i],Min[i-coin[j]]+1); 17 } 18 } 19 /*void print_ans(int *coin_path,int s)// Print combination 20 { 21 while(s) 22 { 23 cout<<Min_path[s]<<' '; 24 s=s-Min_path[s]; 25 } 26 }*/ 27 int main() 28 { 29 ios::sync_with_stdio(false); 30 int s; 31 ans();// The meter 32 cin>>s; 33 cout<<Min[s]<<endl; 34 //print_ans(Min_path,s); 35 return 0; 36 }
But for all the coin problems , It can't be solved like this .
2. The general meaning of all coin questions is as follows （HDUOJ2069, however HDUOJ I can't get in ）：
Yes n Grow coins , The face value is still the same as the previous barabara , In the end, it's different , It is required to output all coin combinations .
Our bureau adopts dp To solve , use dp[i][j] When the amount is i The least you need is j Coin .
dp[0][0] yes 0, that dp[1][1] Namely dp[1-1][1-1]+1, Draw a picture to show ：
Then we can make an analogy dp[i][j]=min(dp[i][j],dp[i-coin[k]][j-1]
You can see ,dp[i][j] The sum of the results of the ordinates is the combination of the least coins .
The code is as follows ：
1 #include<bits/stdc++.h> 2 using namespace std; 3 int ans[251]; 4 int coin[5]={1,5,10,25,50}; 5 int dp[251][101]; 6 void solve() 7 { 8 dp[0][0]=1;//0 element 0 A coin is a plan 9 for(int i=0;i<5;i++) 10 { 11 for(int j=1;j<101;j++)// The number of coins does not exceed 100 12 { 13 for(int k=coin[i];k<251;k++) 14 { 15 dp[k][j]+=dp[k-coin[i]][j-1]; 16 } 17 } 18 } 19 } 20 int main() 21 { 22 int s; 23 solve(); 24 cin>>s; 25 for(int i=0;i<251;i++) 26 { 27 for(int j=0;j<101;j++) 28 { 29 ans[i]+=dp[i][j]; 30 } 31 } 32 cout<<ans[s]<<endl; 33 }
This is the basic dp introduce , The coin problem is solved .
sdutoj
There is a minimum coin problem ：https://acm.sdut.edu.cn/onlinejudge3/problems/1725?from=%2Fsets%2F17
But this is not dp The simple introduction of , This belongs to multiple backpacks ~~~
