当前位置:网站首页>Manually implement heap sorting -838 Heap sort
Manually implement heap sorting -838 Heap sort
2022-07-05 04:41:00 【The wind is a little strong】
Heap properties
Pile up (Heap) Is a kind of data structure , They have a tree structure , And it can ensure that the parent node is larger than the child node ( Or small ). When the root node saves the maximum value in the heap , be called Big root pile ; conversely , It is called a Heap .
Binary heap (Binary Heap) It's the simplest 、 Common heap , It is a tree that conforms to the nature of heap Perfect binary tree . It can achieve O(logn) Insert or delete a value , also O(1) Query the largest ( Or the smallest ) value .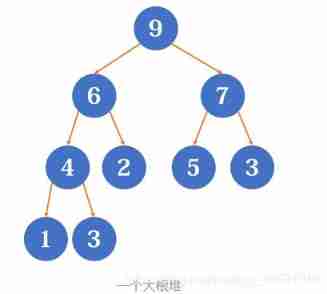
Storage
Take the small root pile for example
As a complete binary tree , A binary stack can be used 1-index To store , For the node p,p2 That is, the left son ,p2+1 That is, the right node . meanwhile , use size Record the number of nodes in the current binary heap .
The relevant operation
up(int x): Compare with the root node of the current node , If the current point is smaller than the root node , Exchange with the root node
down(int x): Compare with the left and right sons of the current node , If the left and right sons are a little smaller than the current , Then exchange the younger son with the current point 
Templates
// h[N] Store values in the heap , h[1] It's the top of the pile ,x My left son is 2x, The right son is 2x + 1
// ph[k] Store the k The position of an insertion point in the heap
// hp[k] The subscript in the heap is k Which point is inserted
int h[N], ph[N], hp[N], size;
// Swap two points , And its mapping relationship
void heap_swap(int a, int b)
{
swap(ph[hp[a]],ph[hp[b]]);
swap(hp[a], hp[b]);
swap(h[a], h[b]);
}
void down(int u)
{
int t = u;
if (u * 2 <= size && h[u * 2] < h[t]) t = u * 2;
if (u * 2 + 1 <= size && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
if (u != t)
{
heap_swap(u, t);
down(t);
}
}
void up(int u)
{
while (u / 2 && h[u] < h[u / 2])
{
heap_swap(u, u / 2);
u >>= 1;
}
}
// O(n) Building the heap
for (int i = n / 2; i; i -- ) down(i);
subject

Code
#include<iostream>
#include<algorithm>
using namespace std;
const int N=100005;
int h[N],len;
int n,m;
void down(int u){
int t=u; //t Save the subscript of the lowest decimal
if(2*u<=len && h[2*u]<h[t]){
// Subscript to be u My point has a left son , The left son is smaller
t=2*u; // The youngest is the left son
}
if(2*u+1<=len && h[2*u+1]<h[t]){
// Subscript to be u The right son of is smaller than the current youngest
t=2*u+1; // The youngest is the right son
}
if(u!=t){
// If the current value is not the minimum , So update
swap(h[u],h[t]); // Exchange the smallest to u The location of
down(t); // Recursive current (2u+1) The following values
}
}
void up(int u){
if(u/2>=1 && h[u/2]>h[u]){
// There is a parent node ,
swap(h[u/2],h[u]);
up(u/2);
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>h[i];
}
len=n;
for(int i=n/2;i>0;i--){
// Because the last layer has no child nodes , So just cycle n/2 That's it .
down(i);
}
while(m--){
cout<<h[1]<<" ";
h[1]=h[len]; // After taking out the minimum value , Put the last value in the first position , Total number minus one , then down
len--;
down(1);
}
return 0;
}
Reference resources Algorithm learning notes (47): Binary heap
边栏推荐
- PHP读取ini文件并修改内容写入
- All in one 1413: determine base
- Group counting notes (1) - check code, original complement multiplication and division calculation, floating point calculation
- English topic assignment (26)
- Variable category (automatic, static, register, external)
- Construction d'un Cluster redis sous Windows
- Neural networks and deep learning Chapter 3: linear model reading questions
- MacBook installation postgresql+postgis
- 官宣!第三届云原生编程挑战赛正式启动!
- Function (basic: parameter, return value)
猜你喜欢

Wan broadband access technology V EPON Technology

CUDA Programming atomic operation atomicadd reports error err:msb3721, return code 1
![[illusory engine UE] method to realize close-range rotation of operating objects under fuzzy background and pit recording](/img/11/b55f85ef9e1f22254218cb9083b823.png)
[illusory engine UE] method to realize close-range rotation of operating objects under fuzzy background and pit recording

2022-2028 global and Chinese virtual data storage Market Research Report

Web开发人员应该养成的10个编程习惯
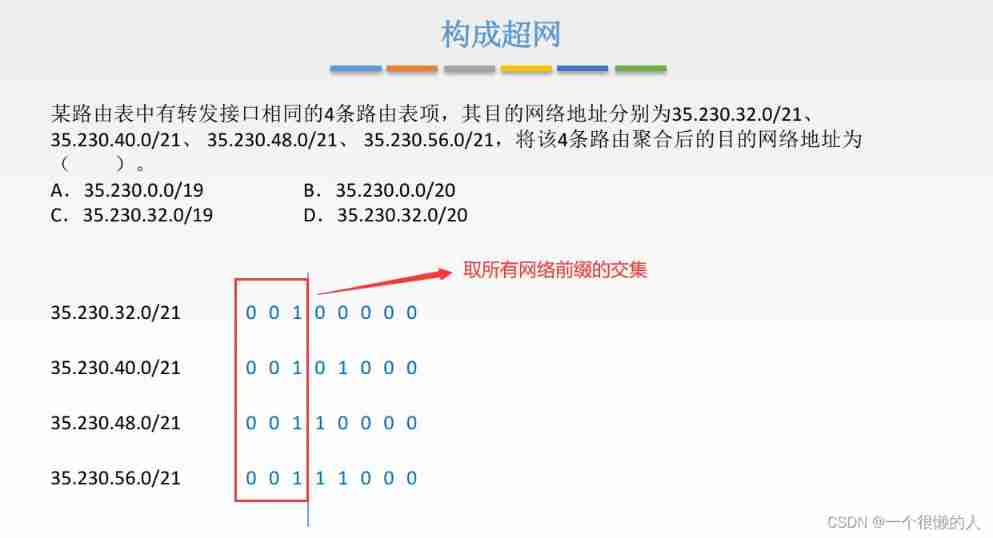
Network layer - forwarding (IP, ARP, DCHP, ICMP, network layer addressing, network address translation)

TPG x AIDU|AI领军人才招募计划进行中!

10 programming habits that web developers should develop

官宣!第三届云原生编程挑战赛正式启动!
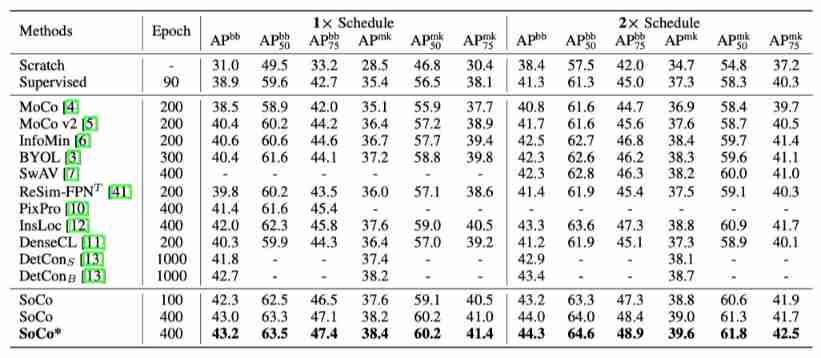
Moco is not suitable for target detection? MsrA proposes object level comparative learning target detection pre training method SOCO! Performance SOTA! (NeurIPS 2021)...
随机推荐
Power management bus (pmbus)
首席信息官如何利用业务分析构建业务价值?
Decryption function calculates "task state and lifecycle management" of asynchronous task capability
[groovy] closure (closure as function parameter | code example)
Private collection project practice sharing [Yugong series] February 2022 U3D full stack class 006 unity toolbar
CSDN body auto generate directory
函数(易错)
Observable time series data downsampling practice in Prometheus
Sword finger offer 04 Search in two-dimensional array
Neural networks and deep learning Chapter 2: machine learning overview reading questions
Moco is not suitable for target detection? MsrA proposes object level comparative learning target detection pre training method SOCO! Performance SOTA! (NeurIPS 2021)...
OWASP top 10 vulnerability Guide (2021)
This is an age of uncertainty
JMeter -- distributed pressure measurement
Neural networks and deep learning Chapter 5: convolutional neural networks reading questions
Network layer - forwarding (IP, ARP, DCHP, ICMP, network layer addressing, network address translation)
Is there a sudden failure on the line? How to make emergency diagnosis, troubleshooting and recovery
Debug insights
解密函数计算异步任务能力之「任务的状态及生命周期管理」
Label exchange experiment