当前位置:网站首页>概率论与数理统计考试重点复习路线
概率论与数理统计考试重点复习路线
2022-07-05 04:17:00 【物联黄同学】
概率论与数理统计考试重点复习路线
文章目录
前言
希望能够通过一份简单的路线,实现精准高效的备战明天的考试。话不多说,冲冲冲!
内容分为概率论与数理统计两个部分,中间的串联是第五章的大数定律和中心极限定理。
MindMap
概率论部分
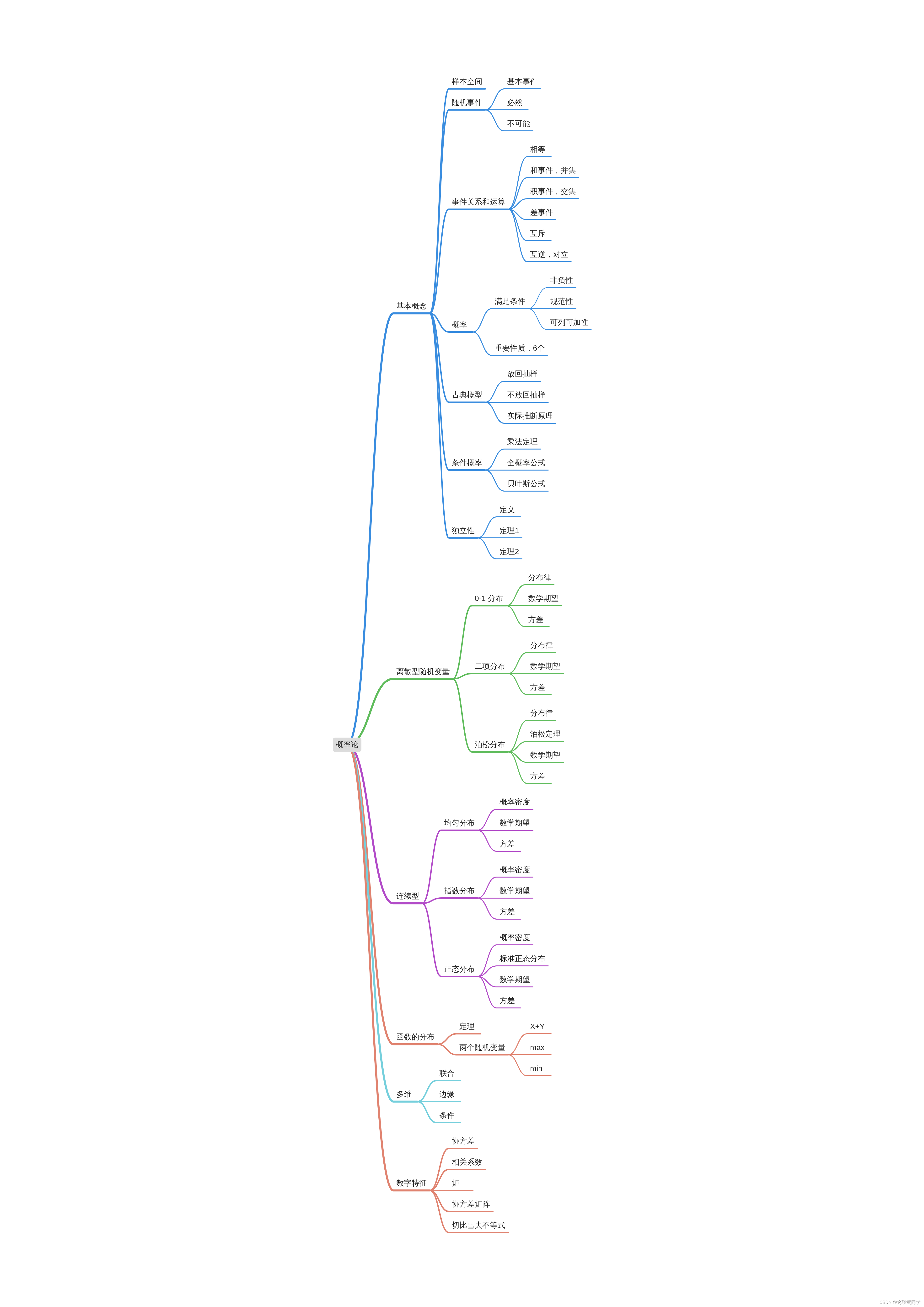
数理统计部分
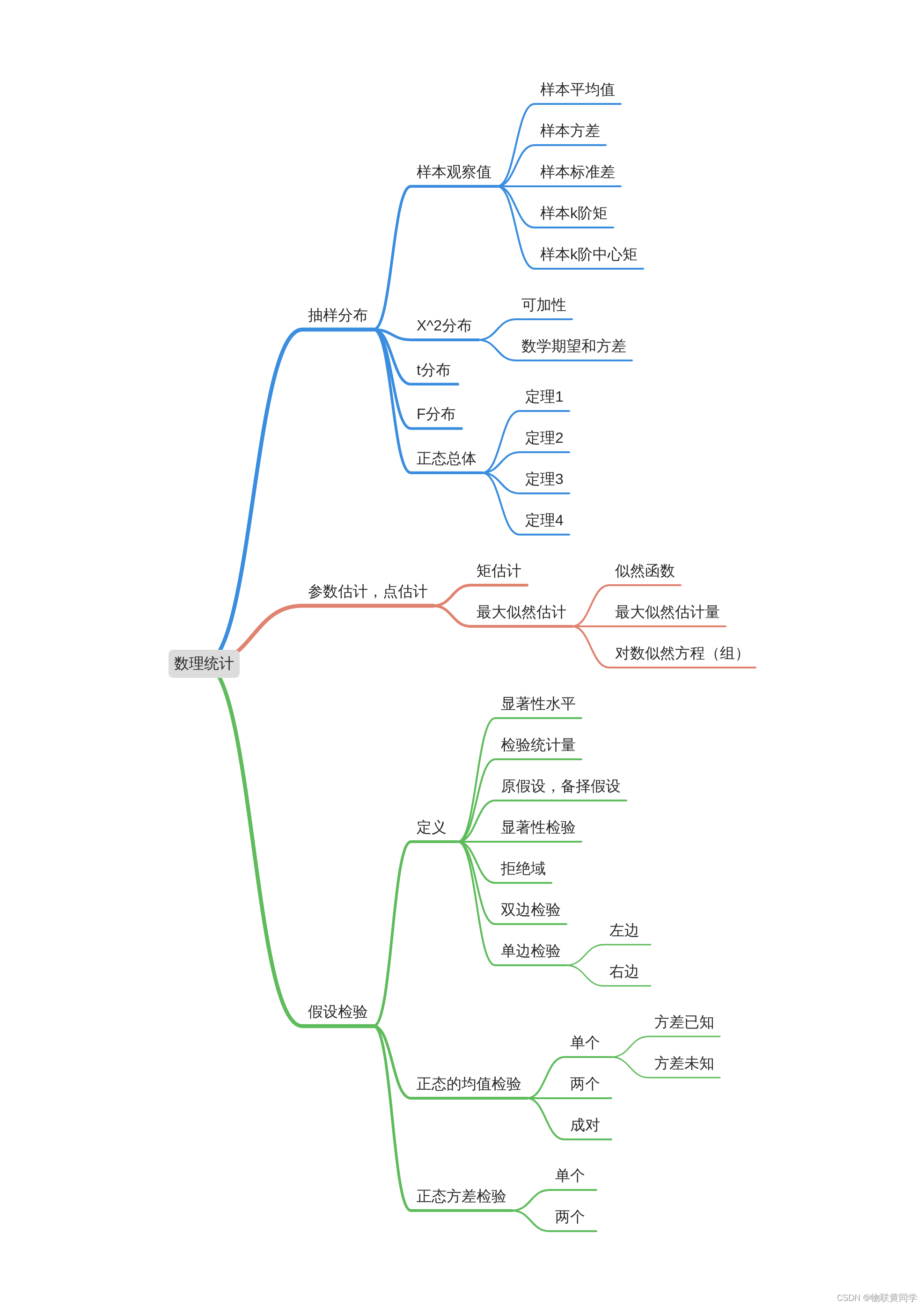
概率论
基本概念
这个部分的内容,我的建议是直接看我之前的blog,或者看书以及其他网课ppt之类的。
关于随机变量的分布函数我不去列举,大家可以直接通过分布律或者概率密度推导
离散型
0-1 分布
X~b§
分布律
P { X = k } = p k ( 1 − p ) 1 − k , k = 1 , 0 P\{X=k \} = p^k(1-p)^{1-k}, \qquad k = 1, 0 P{ X=k}=pk(1−p)1−k,k=1,0
| X | 0 | 1 |
|---|---|---|
| p_k | 1-p | p |
数学期望
E ( X ) = p E(X) = p E(X)=p
方差
D ( X ) = ( 1 − p ) ⋅ p D(X) = (1-p)\cdot p D(X)=(1−p)⋅p
二项分布
X~b(n, p)
分布律
P { X = k } = p k ( 1 − p ) 1 − k P\{X=k \} = p^k(1-p)^{1-k} P{ X=k}=pk(1−p)1−k
数学期望
E ( X ) = n p E(X) = np E(X)=np
方差
D ( X ) = n ( 1 − p ) ⋅ p D(X) = n(1-p)\cdot p D(X)=n(1−p)⋅p
泊松分布
X~π(λ)
分布律
P { X = k } = λ k e − λ k ! , k = 0 , 1 , 2... P\{X=k \} = \frac{\lambda^ke^{-\lambda}}{k!}, \qquad k=0,1,2... P{ X=k}=k!λke−λ,k=0,1,2...
泊松定理
就是用泊松去逼近二项,np=λ
lim n → ∞ C n k ( 1 − p n ) n − k = λ k e − λ k ! \lim_{n\rightarrow \infty}{C_n^k(1-p_n)^{n-k}} = \frac{\lambda^ke^{-\lambda}}{k!} n→∞limCnk(1−pn)n−k=k!λke−λ
数学期望
E ( X ) = λ E(X) = \lambda E(X)=λ
方差
D ( X ) = λ D(X) = \lambda D(X)=λ
连续型
均匀分布
X~U(a, b)
概率密度
KaTeX parse error: No such environment: align at position 26: …eft \{ \begin{̲a̲l̲i̲g̲n̲}̲ &\frac{1}{b…
期望
E ( X ) = a + b 2 E(X) = \frac {a+b}{2} E(X)=2a+b
方差
D ( X ) = ( b − a ) 2 12 D(X) = \frac{(b-a)^2}{12} D(X)=12(b−a)2
指数分布
X~E(θ)
概率密度
KaTeX parse error: No such environment: align at position 26: …eft \{ \begin{̲a̲l̲i̲g̲n̲}̲ &\frac{1}{\…
期望
E ( X ) = θ E(X) = \theta E(X)=θ
方差
D ( X ) = θ 2 D(X) = \theta^2 D(X)=θ2
正态分布
X~N(μ, σ)
概率密度
f ( x ) = 1 2 π σ e − ( x − u ) 2 2 σ 2 , − ∞ < x < ∞ f(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-u)^2}{2\sigma^2}}, \qquad -\infty < x < \infty f(x)=2πσ1e−2σ2(x−u)2,−∞<x<∞
标准正态分布
X ∼ N ( 0 , 1 2 ) φ ( x ) = 1 2 π e − x 2 / 2 X\sim N(0, 1^2)\\ \varphi(x) = \frac{1}{\sqrt{2\pi}}e^{-x^2/2} X∼N(0,12)φ(x)=2π1e−x2/2
期望和方差,一般情况下只要先化成标准正态分布,然后用标准的正态分布的方差和期望求解即可。
期望
E ( x ) = μ E(x) = \mu E(x)=μ
方差
D ( X ) = σ 2 D(X) = \sigma^2 D(X)=σ2
概率论部分的除了这些其实还有像随机变量函数,多维的边缘和条件以及联合,还有第四章的协方差和矩。但是这些内容我就不提了,有需要的可以看blog或者课本。
数理统计
开摆了,这个直接看吧。我要回去睡觉了。
边栏推荐
- MacBook installation postgresql+postgis
- Sequelize. JS and hasmany - belongsto vs hasmany in serialize js
- provide/inject
- Containerd series - what is containerd?
- Online text line fixed length fill tool
- lds链接的 顺序问题
- 10种寻址方式之间的区别
- The new project Galaxy token just announced by coinlist is gal
- Use of vscode software
- Use Firefox browser to quickly pick up Web image materials
猜你喜欢
Online sql to excel (xls/xlsx) tool
![[understand series after reading] 6000 words teach you to realize interface automation from 0 to 1](/img/eb/c944d4a71ce30589e71059ed848899.png)
[understand series after reading] 6000 words teach you to realize interface automation from 0 to 1

Ctfshow web entry code audit
Online text line fixed length fill tool

基于TCP的移动端IM即时通讯开发仍然需要心跳保活

About the recent experience of writing questions
![[phantom engine UE] the difference between running and starting, and the analysis of common problems](/img/e2/49d6c4777c12e9f4e3f8b6ca6db41c.png)
[phantom engine UE] the difference between running and starting, and the analysis of common problems
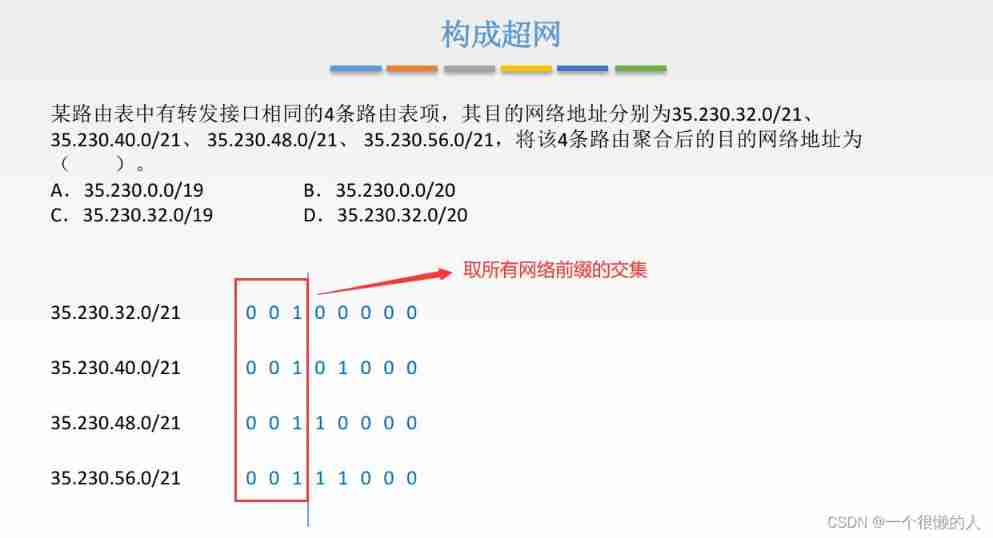
Network layer - forwarding (IP, ARP, DCHP, ICMP, network layer addressing, network address translation)
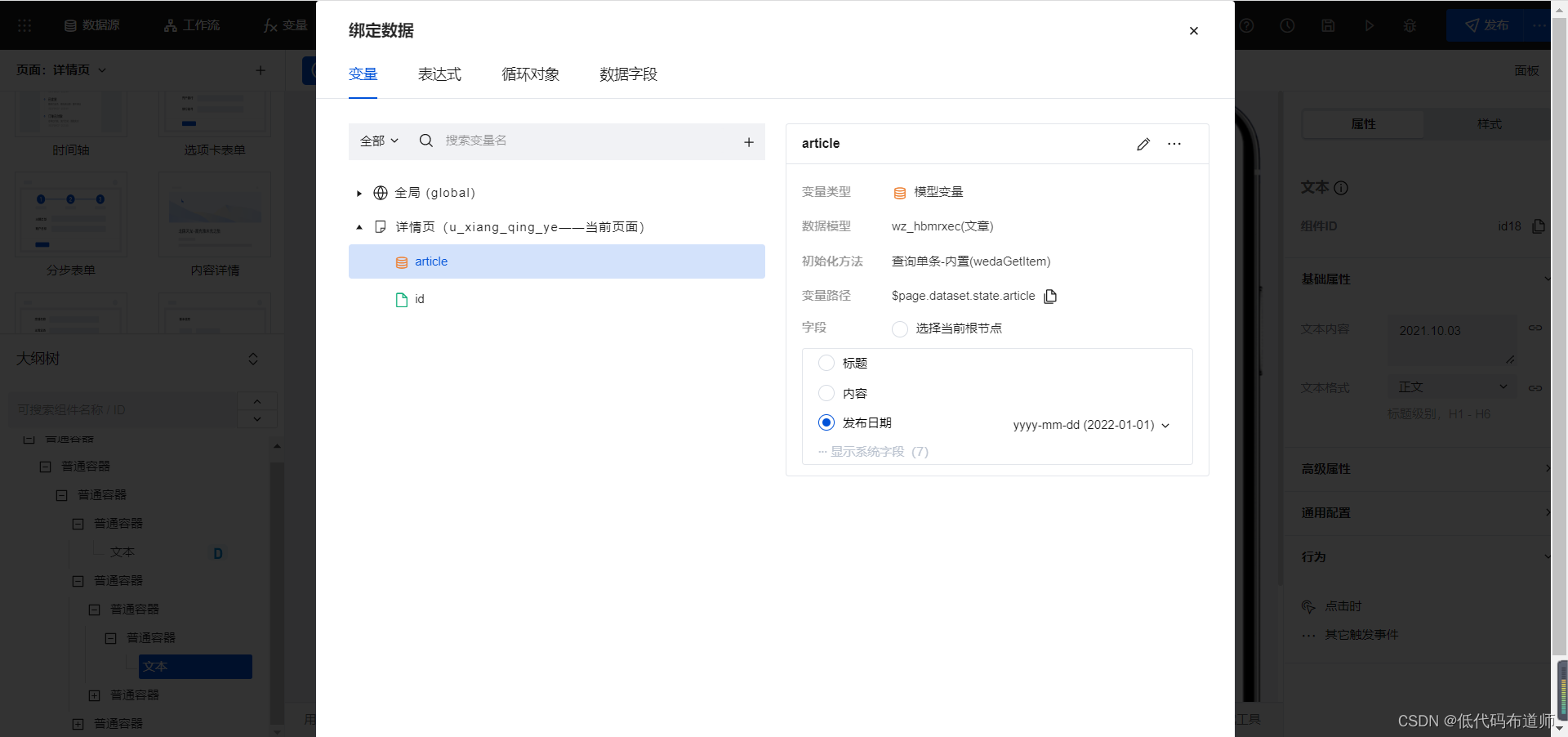
小程序中实现文章的关注功能
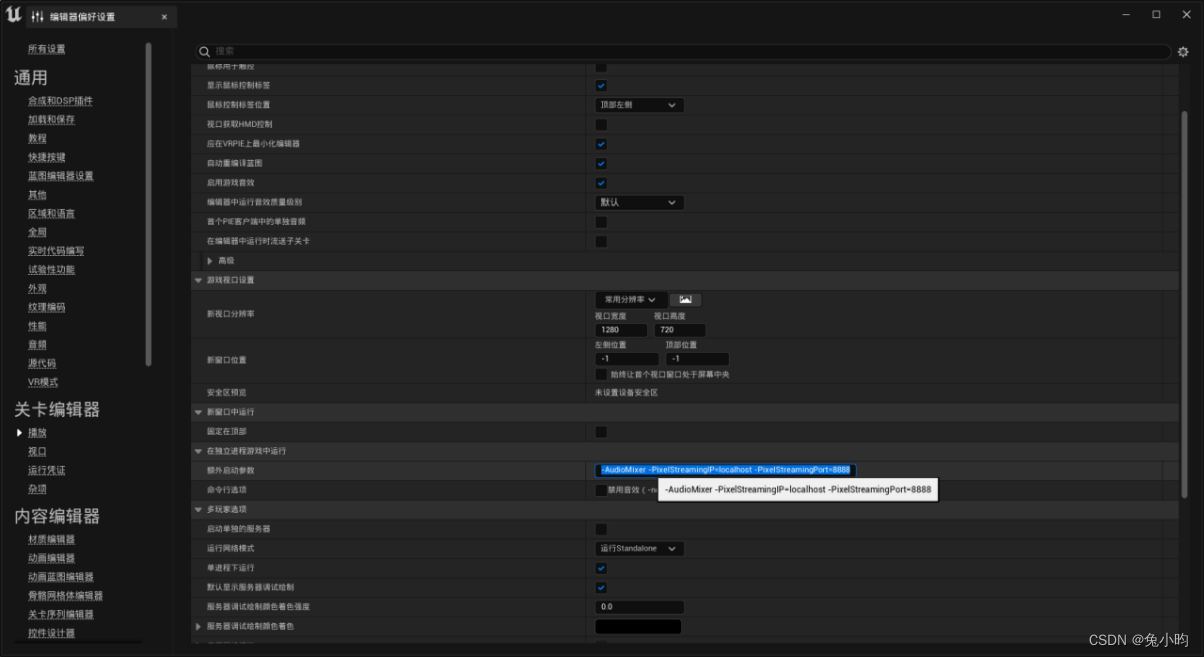
【虚幻引擎UE】实现UE5像素流部署仅需六步操作少走弯路!(4.26和4.27原理类似)
随机推荐
【虚幻引擎UE】实现测绘三脚架展开动画制作
Interview byte, pass the exam and directly work on three sides. As a result, I found an architect to hang me?
蛇形矩阵
[uniapp] system hot update implementation ideas
[phantom engine UE] realize the animation production of mapping tripod deployment
Threejs loads the city obj model, loads the character gltf model, and tweetjs realizes the movement of characters according to the planned route
provide/inject
Number of possible stack order types of stack order with length n
Uni app common functions /api
Sequelize. JS and hasmany - belongsto vs hasmany in serialize js
A real day for Beijing programmers!!!!!
【虚幻引擎UE】实现UE5像素流部署仅需六步操作少走弯路!(4.26和4.27原理类似)
Threejs Internet of things, 3D visualization of farms (I)
How to remove installed elpa package
Summary of scene design
[phantom engine UE] package error appears! Solutions to findpin errors
【虚幻引擎UE】实现背景模糊下近景旋转操作物体的方法及踩坑记录
Moco is not suitable for target detection? MsrA proposes object level comparative learning target detection pre training method SOCO! Performance SOTA! (NeurIPS 2021)...
A application wakes up B should be a fast method
我国算力规模排名全球第二:计算正向智算跨越