当前位置:网站首页>Key review route of probability theory and mathematical statistics examination
Key review route of probability theory and mathematical statistics examination
2022-07-05 04:23:00 【IOT classmate Huang】
The key review route of probability theory and mathematical statistics exam
List of articles
Preface
Hope to pass a simple route , Achieve accurate and efficient preparation for tomorrow's exam . Don't talk much , To rush !
The content is divided into two parts: probability theory and mathematical statistics , The middle series is the law of large numbers and central limit theorem in Chapter 5 .
MindMap
Probability theory part
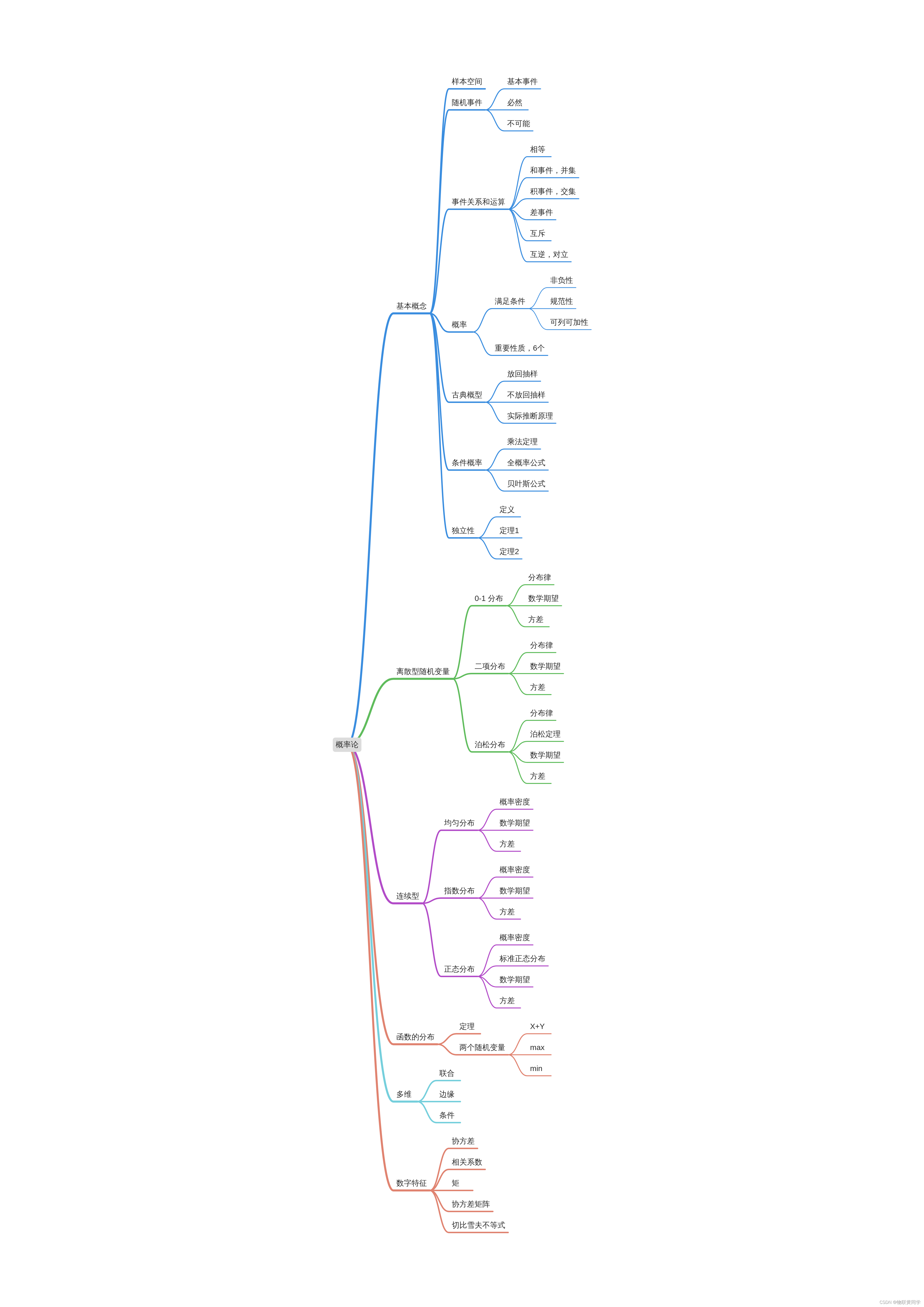
Mathematical statistics
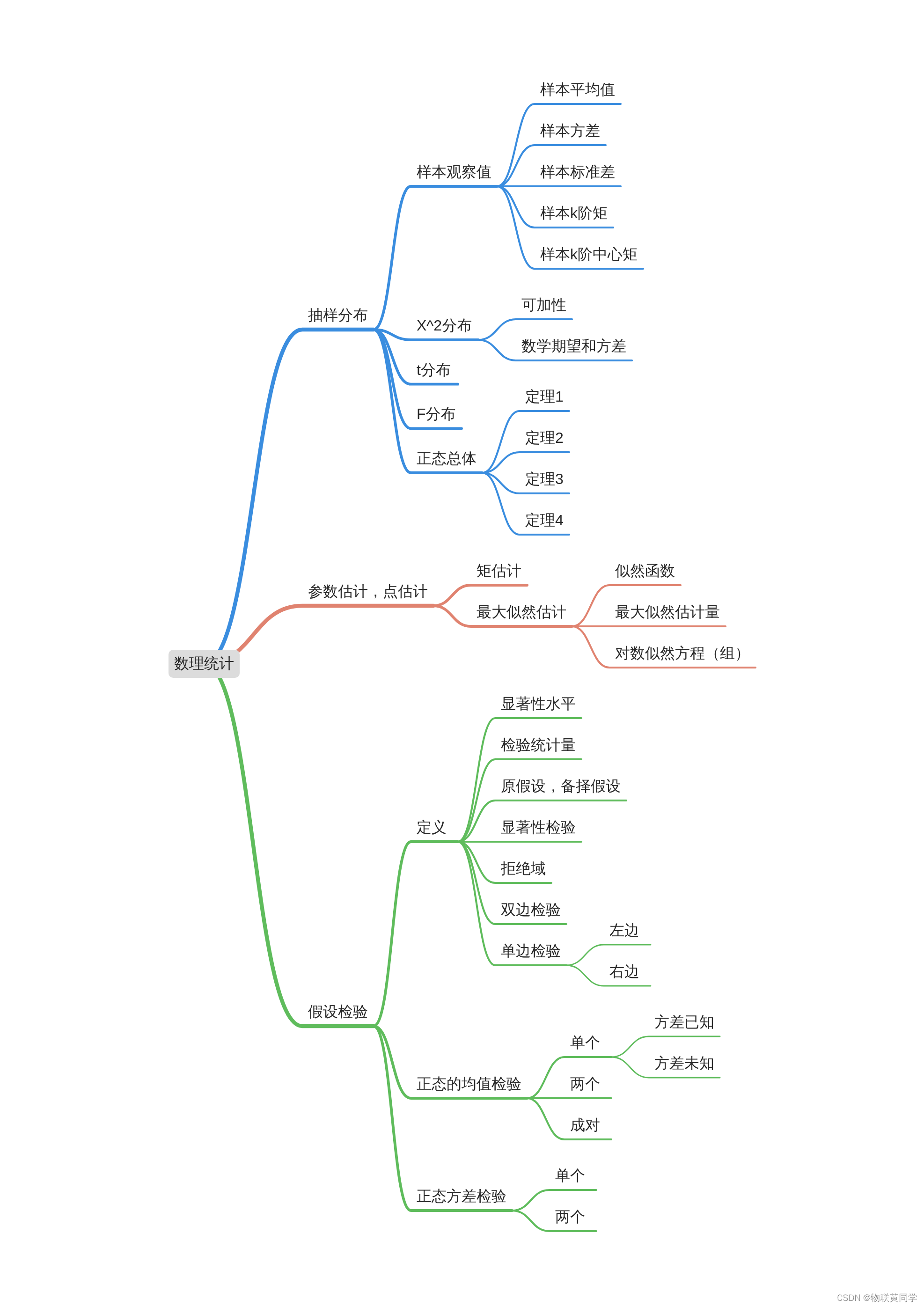
probability theory
Basic concepts
The content of this part , My suggestion is to look directly at my previous blog, Or reading books and other online classes ppt And so on. .
I won't enumerate the distribution function of random variables , You can deduce it directly through the distribution law or probability density
discrete
0-1 Distribution
X~b§
Distribution law
P { X = k } = p k ( 1 − p ) 1 − k , k = 1 , 0 P\{X=k \} = p^k(1-p)^{1-k}, \qquad k = 1, 0 P{ X=k}=pk(1−p)1−k,k=1,0
| X | 0 | 1 |
|---|---|---|
| p_k | 1-p | p |
Mathematical expectation
E ( X ) = p E(X) = p E(X)=p
variance
D ( X ) = ( 1 − p ) ⋅ p D(X) = (1-p)\cdot p D(X)=(1−p)⋅p
The binomial distribution
X~b(n, p)
Distribution law
P { X = k } = p k ( 1 − p ) 1 − k P\{X=k \} = p^k(1-p)^{1-k} P{ X=k}=pk(1−p)1−k
Mathematical expectation
E ( X ) = n p E(X) = np E(X)=np
variance
D ( X ) = n ( 1 − p ) ⋅ p D(X) = n(1-p)\cdot p D(X)=n(1−p)⋅p
Poisson distribution
X~π(λ)
Distribution law
P { X = k } = λ k e − λ k ! , k = 0 , 1 , 2... P\{X=k \} = \frac{\lambda^ke^{-\lambda}}{k!}, \qquad k=0,1,2... P{ X=k}=k!λke−λ,k=0,1,2...
Poisson's theorem
Is to use Poisson to approximate binomial ,np=λ
lim n → ∞ C n k ( 1 − p n ) n − k = λ k e − λ k ! \lim_{n\rightarrow \infty}{C_n^k(1-p_n)^{n-k}} = \frac{\lambda^ke^{-\lambda}}{k!} n→∞limCnk(1−pn)n−k=k!λke−λ
Mathematical expectation
E ( X ) = λ E(X) = \lambda E(X)=λ
variance
D ( X ) = λ D(X) = \lambda D(X)=λ
Continuous type
Uniform distribution
X~U(a, b)
Probability density
KaTeX parse error: No such environment: align at position 26: …eft \{ \begin{̲a̲l̲i̲g̲n̲}̲ &\frac{1}{b…
expect
E ( X ) = a + b 2 E(X) = \frac {a+b}{2} E(X)=2a+b
variance
D ( X ) = ( b − a ) 2 12 D(X) = \frac{(b-a)^2}{12} D(X)=12(b−a)2
An index distribution
X~E(θ)
Probability density
KaTeX parse error: No such environment: align at position 26: …eft \{ \begin{̲a̲l̲i̲g̲n̲}̲ &\frac{1}{\…
expect
E ( X ) = θ E(X) = \theta E(X)=θ
variance
D ( X ) = θ 2 D(X) = \theta^2 D(X)=θ2
Normal distribution
X~N(μ, σ)
Probability density
f ( x ) = 1 2 π σ e − ( x − u ) 2 2 σ 2 , − ∞ < x < ∞ f(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-u)^2}{2\sigma^2}}, \qquad -\infty < x < \infty f(x)=2πσ1e−2σ2(x−u)2,−∞<x<∞
Standard normal distribution
X ∼ N ( 0 , 1 2 ) φ ( x ) = 1 2 π e − x 2 / 2 X\sim N(0, 1^2)\\ \varphi(x) = \frac{1}{\sqrt{2\pi}}e^{-x^2/2} X∼N(0,12)φ(x)=2π1e−x2/2
Expectation and variance , In general, as long as it is converted into a standard normal distribution , Then it can be solved with the variance and expectation of the standard normal distribution .
expect
E ( x ) = μ E(x) = \mu E(x)=μ
variance
D ( X ) = σ 2 D(X) = \sigma^2 D(X)=σ2
In addition to these, there are actually random variable functions in probability theory , Multi dimensional edges and conditions and combinations , There are also covariance and moments in Chapter 4 . But I won't mention these contents , If necessary, you can see blog Or textbooks .
mathematical statistics
It's swinging , Look at this directly . I'm going back to bed .
边栏推荐
- Sword finger offer 07 Rebuild binary tree
- Threejs realizes rain, snow, overcast, sunny, flame
- 函数(基本:参数,返回值)
- Convert Boolean to integer value PHP - Convert Boolean to integer value PHP
- Threejs Internet of things, 3D visualization of farms (I)
- Hexadecimal to decimal
- MacBook installation postgresql+postgis
- [popular science] basic knowledge of thermal design: heat dissipation analysis of 5g optical devices
- [phantom engine UE] only six steps are needed to realize the deployment of ue5 pixel stream and avoid detours! (the principles of 4.26 and 4.27 are similar)
- A real day for Beijing programmers!!!!!
猜你喜欢
Rome chain analysis
Alibaba cloud ECS uses cloudfs4oss to mount OSS
![[popular science] basic knowledge of thermal design: heat dissipation analysis of 5g optical devices](/img/45/380e739f5eed33626c363756f814d3.png)
[popular science] basic knowledge of thermal design: heat dissipation analysis of 5g optical devices
![[phantom engine UE] realize the animation production of mapping tripod deployment](/img/89/351641c3da7e2acdbf389bc298b75e.png)
[phantom engine UE] realize the animation production of mapping tripod deployment
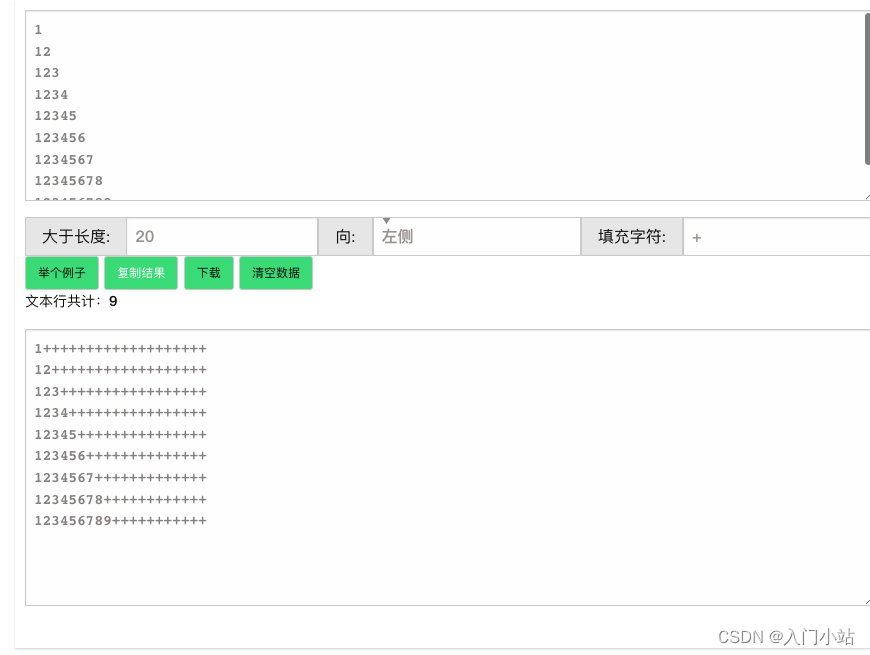
Online text line fixed length fill tool
小程序中实现文章的关注功能

【虚幻引擎UE】实现测绘三脚架展开动画制作

Threejs factory model 3DMAX model obj+mtl format, source file download

Kwai, Tiktok, video number, battle content payment
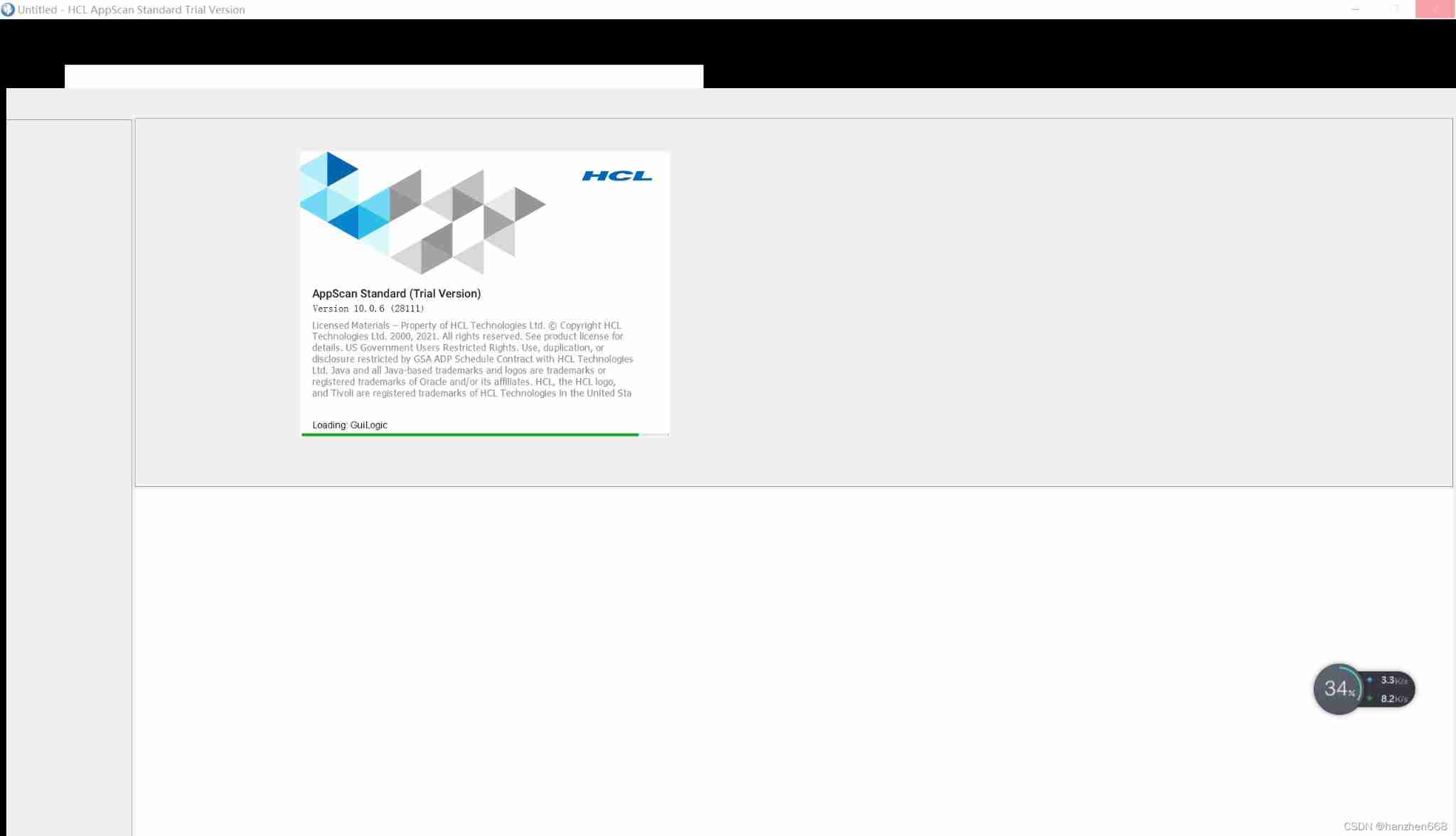
About the prompt loading after appscan is opened: guilogic, it keeps loading and gets stuck. My personal solution. (it may be the first solution available in the whole network at present)
随机推荐
Use threejs to create geometry and add materials, lights, shadows, animations, and axes
Threejs Internet of things, 3D visualization of farms (I)
Rust blockchain development - signature encryption and private key public key
自动语音识别(ASR)研究综述
[moteur illusoire UE] il ne faut que six étapes pour réaliser le déploiement du flux de pixels ue5 et éviter les détours! (4.26 et 4.27 principes similaires)
Sword finger offer 04 Search in two-dimensional array
Threejs realizes the drawing of the earth, geographical location annotation, longitude and latitude conversion of world coordinates threejs coordinates
C26451: arithmetic overflow: use the operator * on a 4-byte value, and then convert the result to an 8-byte value. To avoid overflow, cast the value to wide type before calling the operator * (io.2)
PR video clip (project packaging)
open graph协议
包 类 包的作用域
Decimal to hexadecimal
C language course setting: cinema ticket selling management system
Threejs realizes sky box, panoramic scene, ground grass
WeNet:面向工业落地的E2E语音识别工具
首席信息官如何利用业务分析构建业务价值?
函數(易錯)
Burpsuite grabs app packets
【虛幻引擎UE】實現UE5像素流部署僅需六步操作少走彎路!(4.26和4.27原理類似)
[finebi] the process of making custom maps using finebi