Hands on deep learning (34) -- sequence model

Sequence model

One 、 What is a sequence model

   Imagine you are watching Netflix（ A foreign video website ） The movie on . As a great Netflix user , You decide to comment on every movie . After all , A good movie deserves the title of a good movie , And you want to see more good movies , Right ？ The fact proved that , It's not that simple . as time goes on , People's views on movies will change a lot . in fact , Psychologists even name some effects ：

• Anchoring （anchoring）, Based on others' opinions . for example , After the Oscars , The ratings of films that get attention will rise , Although it's still the original movie . This effect will last for several months , Until people forget the awards the film once won . It turns out that , This effect will increase the score by more than half a percentage point （Wu.Ahmed.Beutel.ea.2017）.
• Hedonic adaptation （hedonic adaption）, That is, human beings quickly accept and adapt to a better or worse situation as the new normal . for example , After watching a lot of good movies , People expect the next film to be equally good or better . therefore , After seeing many wonderful movies , Even an ordinary movie can be considered bad .
• Seasonality （seasonality）. Few viewers like watching Santa Claus movies in August .
• occasionally , Movies can become unpopular because of the misconduct of directors or actors in production .
• Some films can only become minority films because they are extremely bad .Plan 9 from Outer Space and Troll 2 That's why it's notorious .

   In short , Film ratings are by no means fixed . therefore , Using time dynamics can get more accurate movie recommendations :（Koren.2009） . Of course , Sequence data is not just about movie ratings . More scenarios are given below .

• Many users have strong specific habits when using applications . for example , Social media apps are more popular after school . When the market is open, stock market trading software is more commonly used .
• It is more difficult to predict tomorrow's share price than to make up for yesterday's lost share price , Although both are only estimates of one number . After all , Foresight is much harder than hindsight . In statistics , The former （ Predictions that exceed known observations ） be called extrapolation （extrapolation）, While the latter （ Estimate between existing observations ） be called Insert （interpolation）.
• In essence, music 、 voice 、 Text and video are continuous . If we rearrange them , They will lose their meaning . Text title “ Dog bites man ” Far from it “ Man bites dog ” So amazing , Although the words that make up the two sentences are exactly the same .
• Earthquakes have a strong correlation , That is, after the great earthquake , There are likely to be several smaller aftershocks , These aftershocks are much larger than those without strong earthquakes . in fact , Earthquakes are spatiotemporal , in other words , Aftershocks usually occur in a short time span and close distance .
• Human interaction is also continuous , This can be seen from the quarrels and debates on twitter .

summary ：

1. In the time series model , The current data is related to previous observations
2. Autoregressive models use their own past data to predict the future
3. Markov model assumes that the current data is only related to the latest few data
4. Latent variable model uses latent variables to summarize historical information

Two 、 Statistical tools for sequence models

   We need statistical tools and new deep neural network structures to process sequence data . For the sake of simplicity , Our stock price is shown in the following figure （ Rich time 100 Index ） For example .

   Let's use it $x_t$ It means the price . That is to say Time step （time step）$t\in {\mathbb{Z}}^{+}$ when , The price we observed $x_t$. Please note that , For the sequence in this article ,$t$ Usually discrete , And varies with integers or subsets . Suppose a trader wants to $t$ The Japanese stock market performed well , So I predicted $x_t$：

$$x_t\sim P(x_t\mid x_{t-1},\dots ,x_1).$$

2.1 Autoregressive model

   To achieve this , Traders can use regression models , Let's say we have linear regression model . There is only one major problem ： Input $x_{t-1},\dots ,x_1$ The quantity of is due to $t$ But different . in other words , This number will increase as the amount of data we encounter increases , Therefore, we need an approximate method to make this calculation easy to handle . Much of the rest of this chapter will focus on how to effectively estimate $P(x_t\mid x_{t-1},\dots ,x_1)$ an . In short , It boils down to the following two strategies .

   The first strategy , Suppose a fairly long sequence in reality $x_{t-1},\dots ,x_1$ It may not be necessary , So we only use observation sequences $x_{t-1},\dots ,x_{t-\tau }$, And it is satisfied that the time span is $\tau$. Now? , The most direct benefit is for $t>\tau$ The number of parameters is always the same , This enables us to train a deep network mentioned above . This model is called Autoregressive model （autoregressive models）, Because they are returning to themselves .

   The second strategy , As shown in the figure below , It is to retain the total of some past observations $h_t$, Besides prediction ${\hat{x}}_t$ It is also updated $h_t$. This produces estimates $x_t$ and ${\hat{x}}_t=P(x_t\mid h_t)$ Model of , And updated $h_t=g(h_{t-1},x_{t-1})$. because $h_t$ Never observed , This kind of model is also called Implicit variable autoregressive model （latent autoregressive models）.

   There is an obvious problem in both cases , That is, how to generate training data . A classic method is to use historical observations to predict the next observation . obviously , We don't expect time to stagnate . However , A common assumption is that the dynamics of the sequence itself will not change , Although the specific value $x_t$ May change . This assumption is reasonable , Because the new dynamics must be affected by the new data , And we can't use the data we have now to predict the new dynamics . Statisticians call invariant dynamics Still （stationary）. therefore , No matter what we do , The estimated value of the whole sequence will be obtained in the following way

$$P(x_1,\dots ,x_T)=\prod _{t=1}^{T}P(x_t\mid x_{t-1},\dots ,x_1).$$

   Be careful , If we deal with discrete objects ( Like words ), Not consecutive numbers , Then the above considerations are still valid . The only difference is , under these circumstances , We need to use classifiers instead of regression models to estimate $P(x_t\mid x_{t-1},\dots ,x_1)$.

1.2 Markov model

   Think about it , In the approximation method of autoregressive model , We use $x_{t-1},\dots ,x_{t-\tau }$ instead of $x_{t-1},\dots ,x_1$ To estimate $x_t$. As long as this approximation is accurate , Let's say that the sequence satisfies Markov condition （Markov condition）. especially , If $\tau =1$, Get one First order Markov model （first-order Markov model）,$P(x)$ Given by the following formula ：

$$P(x_1,\dots ,x_T)=\prod _{t=1}^{T}P(x_t\mid x_{t-1})\text{ where }P(x_1\mid x_0)=P(x_1).$$

   When $x_t$ When only discrete values are assumed , Such a model is great , Because in this case , Using dynamic programming, the results can be calculated accurately along the Markov chain . for example , We can efficiently calculate $P(x_{t+1}\mid x_{t-1})$：

$$\begin{array}{rl}P(x_{t+1}\mid x_{t-1})& =\frac{{\sum }_{x_t}P(x_{t+1},x_t,x_{t-1})}{P(x_{t-1})}\\ & =\frac{{\sum }_{x_t}P(x_{t+1}\mid x_t,x_{t-1})P(x_t,x_{t-1})}{P(x_{t-1})}\\ & =\sum _{x_t}P(x_{t+1}\mid x_t)P(x_t\mid x_{t-1})\end{array}$$

   Take advantage of this fact , We only need to consider the very short history observed in the past ：$P(x_{t+1}\mid x_t,x_{t-1})=P(x_{t+1}\mid x_t)$. A detailed introduction to dynamic planning is beyond the scope of this section . These tools are widely used in control algorithms and reinforcement learning algorithms .

1.3 Causal relationship

   In principle, , Expand in reverse order $P(x_1,\dots ,x_T)$ it . After all , Based on the conditional probability formula , We can always write ：
$$P(x_1,\dots ,x_T)=\prod _{t=T}^{1}P(x_t\mid x_{t+1},\dots ,x_T).$$

   in fact , If based on a Markov model , We can get an inverse conditional probability distribution . However , in many instances , Data has a natural direction , That is, it is advancing in time . Obviously , Future events cannot affect the past . therefore , If we change $x_t$, We may be able to influence $x_{t+1}$ What will happen in the future , But it cannot affect the past . in other words , If we change $x_t$, The distribution based on past events will not change . therefore , explain $P(x_{t+1}\mid x_t)$ It should be better than explaining $P(x_t\mid x_{t+1})$ More easily . for example , In some cases , For some additive noise $ϵ$, Obviously we can find $x_{t+1}=f(x_t)+ϵ$, And vice versa （Hoyer.Janzing.Mooij.ea.2009） . That's good news , Because this is usually the direction we are interested in estimating . The book written by Peters et al . More on this topic has been explained （Peters.Janzing.Scholkopf.2017） . We only touched its fur .

---

Two 、 Markov Assumption MLP model training

   After reviewing so many statistical tools , Let's try it in practice . First , Generate some data . For the sake of simplicity , We use sine function and some additive noise to generate sequence data , The time step is $1,2,\dots ,1000$.

%matplotlib inline
import torch 
from torch import nn 
from d2l import torch as d2l

T = 1000
time = torch.arange(1,T+1,dtype=torch.float32)
x = torch.sin(0.01*time)+torch.normal(0,0.2,(T,))
d2l.plot(time,[x],'time','x',xlim=[1,1000],figsize=(6,3))

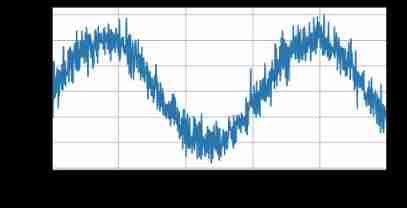
   Next , We need to transform such sequences into features and tags that our model can train . Based on embedded dimension $\tau$, We map the data to $y_t=x_t$ and ${\mathbf{x}}_t=[x_{t-\tau },\dots ,x_{t-1}]$. Astute readers may have noticed , This sample provides less data than ours $\tau$ individual , Because we don't have enough historical records to describe $\tau$ Data samples . A simple solution , Especially if the sequence is long enough, discard these items , Or you can fill the sequence with zeros . ad locum , We only use the pre - 600 individual “ features － label ” Train the .

#  Map data to data pairs , Construct input （996,4）, Use the current value as a label , The first four values are the input of the current value 
tau = 4 
features = torch.zeros((T-tau,tau))
for i in range(tau):
    features[:,i] = x[i:T-tau+i]
labels = x[tau:].reshape((-1,1))

batch_size, n_train = 16, 600
#  Only the front `n_train` Samples for training 
train_iter = d2l.load_array((features[:n_train], labels[:n_train]),batch_size, is_train=True)

Design a simple multi-layer perceptron , There are two fully connected layers ,ReLU Activation function and square loss

#  Initialize network parameters 
def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.xavier_uniform_(m.weight)

def get_net():
    net = nn.Sequential(nn.Linear(4,10),nn.ReLU(),nn.Linear(10,1))
    net.apply(init_weights)
    return net

def train(net,train_iter,loss,epochs,lr):
    trainer = torch.optim.Adam(net.parameters(),lr)
    for epoch in range(epochs):
        for X,y in train_iter:
            trainer.zero_grad()
            l = loss(net(X),y)
            l.backward()
            trainer.step()
        print(f'eopoch {
      epoch + 1},'
              f'loss:{
      d2l.evaluate_loss(net,train_iter,loss):f}')

net = get_net()
loss = nn.MSELoss()
train(net,train_iter,loss,5,0.01)

eopoch 1,loss:0.064053
eopoch 2,loss:0.056895
eopoch 3,loss:0.056115
eopoch 4,loss:0.057444
eopoch 5,loss:0.056819

3、 ... and 、 Model to predict

   Because the training loss is very small , We hope the model will work well . Let's see what this means in practice . The first is to check how well the model predicts what will happen in the next time step , That is to say One step prediction （one-step-ahead prediction）.

onestep_preds = net(features) #  Put all the data into the network for prediction , But in fact, there are many times we need to predict according to the prediction results 
d2l.plot(
    [time, time[tau:]],
    [x.detach().numpy(), onestep_preds.detach().numpy()], 'time', 'x',
    legend=['data', '1-step preds'], xlim=[1, 1000], figsize=(6, 3))

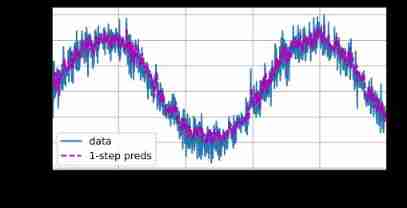
   As we expected, the one-step prediction effect is good . Even if the time steps of these predictions exceed $604$（n_train + tau）, The results still seem credible . However, there is a small problem ： If the time step of the data observation sequence is only $604$, Then we don't expect to receive all the future input predicted one step in advance . contrary , We need to move forward step by step ：
$$\begin{gathered} {\hat{x}}_{605}=f(x_{601},x_{602},x_{603},x_{604}), \\ {\hat{x}}_{606}=f(x_{602},x_{603},x_{604},{\hat{x}}_{605}), \\ {\hat{x}}_{607}=f(x_{603},x_{604},{\hat{x}}_{605},{\hat{x}}_{606}), \\ {\hat{x}}_{608}=f(x_{604},{\hat{x}}_{605},{\hat{x}}_{606},{\hat{x}}_{607}), \\ {\hat{x}}_{609}=f({\hat{x}}_{605},{\hat{x}}_{606},{\hat{x}}_{607},{\hat{x}}_{608}), \\ \dots \end{gathered}$$

   Usually , For until $x_t$ The sequence of observations , It is in the time step ${\hat{x}}_{t+k}$ Predicted output at $t+k$ go by the name of $k$ Next step prediction （$k$-step-ahead-prediction）. Because we have observed $x_{604}$, It leads $k$ The prediction of step is ${\hat{x}}_{604+k}$. let me put it another way , We will have to use our own predictions to make multi-step predictions . Let's see if this is going well .

multistep_preds = torch.zeros(T)
multistep_preds[:n_train + tau] = x[:n_train + tau]
for i in range(n_train + tau, T):
    multistep_preds[i] = net(multistep_preds[i - tau:i].reshape((1, -1)))

d2l.plot([time, time[tau:], time[n_train + tau:]], [
    x.detach().numpy(),
    onestep_preds.detach().numpy(),
    multistep_preds[n_train + tau:].detach().numpy()], 'time', 'x',
         legend=['data', '1-step preds',
                 'multistep preds'], xlim=[1, 1000], figsize=(6, 3))

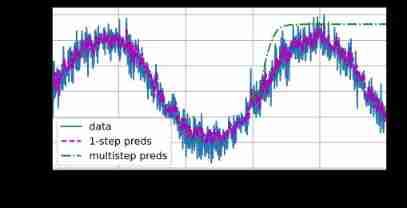
   As the example above shows , It was a huge failure . After a few prediction steps , The prediction result will soon decay to a constant . Why is this algorithm so ineffective ？ The final fact is that Accumulation of errors .

• Suppose in step $1$ after , We accumulate some mistakes ${ϵ}_1=\overline{ϵ}$.
• Now? , step $2$ Of Input （input） Disturbed ${ϵ}_1$, Therefore, the accumulated errors are in order ${ϵ}_2=\overline{ϵ}+c{ϵ}_1$, among $c$ For a constant , The following prediction errors are followed by analogy . So a common phenomenon is that the error may deviate from the real observation results quite quickly .

   for example , future 24 Hourly weather forecasts are often quite accurate , But beyond that , The accuracy will drop rapidly . We will discuss ways to improve this in this chapter and beyond . Let's calculate $k=1,4,16,64$ Let's take a closer look at the prediction of the whole sequence $k$ The difficulty of step prediction .

max_steps = 64
features = torch.zeros((T - tau - max_steps + 1, tau + max_steps))
#  Column  `i` (`i` < `tau`)  Is from  `x`  The observation of 
#  Its time steps from  `i + 1`  To  `i + T - tau - max_steps + 1`
for i in range(tau):
    features[:, i] = x[i:i + T - tau - max_steps + 1]

#  Column  `i` (`i` >= `tau`)  yes  (`i - tau + 1`) Step by step prediction 
#  Its time steps from  `i + 1`  To  `i + T - tau - max_steps + 1`
for i in range(tau, tau + max_steps):
    features[:, i] = net(features[:, i - tau:i]).reshape(-1)

steps = (1, 4, 16, 64)
d2l.plot([time[tau + i - 1:T - max_steps + i] for i in steps],
         [features[:, (tau + i - 1)].detach().numpy() for i in steps], 'time',
         'x', legend=[f'{
      i}-step preds'
                      for i in steps], xlim=[5, 1000], figsize=(6, 3))

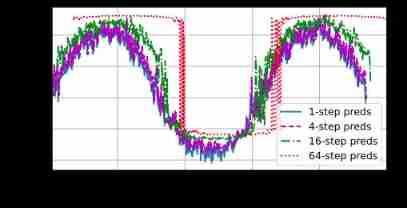
   This clearly shows that when we try to further predict the future , How the quality of prediction changes . although “$4$ Next step prediction ” It still looks good , But any prediction beyond this span is almost useless .

Four 、 summary

• Interpolation and extrapolation differ greatly in difficulty . therefore , When training, always respect the chronological order of the sequence data you have , That is, never train future data .
• The estimation of sequence model needs special statistical tools . Two popular choices are ： Autoregressive model and implicit variable autoregressive model .
• For causal models （ for example , Time moves forward ）, Forward estimation is usually easier than backward estimation .
• For up to time steps $t$ The sequence of observations , It is in the time step $t+k$ The predicted output is "$k$ Next step prediction ". As we further increase the forecast time $k$, Will cause error accumulation , Leading to the decline of prediction quality .