[Li Kou brush questions] 32 Longest valid bracket

Catalog

subject ：

Method 1 ：

Their thinking ：

Code ：

Method 2 ：

Their thinking ：

Code ：

subject ：

Give you one that only contains  '('  and  ')'  String , Find the longest effective （ The format is correct and continuous ） The length of the bracket substring .

Method 1 ：

Their thinking ：

Utilization stack , I learned to use the stack to judge that a contains only '(' and ')' Whether the string of is parenthesized , The solution to that problem is , Traversing the entire string , If it's an open parenthesis, it's on the stack , Is the right parenthesis ① Determine whether the stack has an open bracket and pop up an open bracket ,② If the stack is empty, then false, If all characters are traversed , If there are elements in the stack, they are false, Otherwise true.

Use this idea , Add an array of tags arr, Initialize all elements to 1, What is stored in the stack is the array subscript （ Character index ）. Traversing the entire string , If it is an open parenthesis, the index subscript （i） Join the stack , If it is a right parenthesis, judge whether the element in the stack is empty and if not, pop up , And mark the elements corresponding to the array arr[stack.pop()] And the tag array element corresponding to the current subscript arr[i] Set as 0.

Finally, determine the tag array arr The longest continuous 0 That's all right. .

Code ：

class Solution {
    public int longestValidParentheses(String s) {
        // Find the longest valid bracket 
        // Stack 
        // Use the stack to mark whether the left and right parentheses are valid , The contents of the stack are stored with subscripts i
        Stack<Integer> stack = new Stack<>();
        int[] valid = new int[s.length()];
        for(int i = 0; i < s.length(); i++){
            valid[i] = 1;
        }
        for(int i = 0; i < s.length();i++){
            if(s.charAt(i) == '(') stack.push(i);
            else{
                if(!stack.empty()){
                    valid[i] = 0;
                    valid[stack.pop()] = 0;
                }
            }
        }
        int res = 0,count = 0;
        for(int i = 0; i < s.length();i++){
            if(valid[i] == 1) {
                count = 0;
            }else{
                count++;
            }
            res = Math.max(res,count);
        }
        return res;
    }
}

Method 2 ：

Their thinking ：

Dynamic programming , utilize dp[i] Express By subscript i The length of the longest valid bracket at the end of the character . take dp The array is all initialized to 0. A valid substring must be in ')' ending , With '(' The ending substring corresponds to dp The value must be 0. So we just need to solve it to ')' stay dp The value of the corresponding position in the array . So go through the string from front to back , solve dp value .

①s.charAt(i)=')' And s.charAt(i-1)='(', String is "...()" be dp[i] = dp[i-2]+2.

② If s.charAt(i) = ')' And s.charAt(i-1) = ')', Like strings "...))"->"()(())",

If s.charAt(i - dp[i - 1] - 1)='(', Then the effective bracket length increases the length 2,i The longest valid bracket length of position pair is i-1 The longest bracket length of the position plus the new 2, But you have to Be careful ,i − dp[i − 1] − 1 and i Form a valid pair of parentheses , This will be a paragraph Independent valid parenthesis sequence , If the previous subsequence is shaped like (...)(...) This sequence , Then the longest valid bracket length of the current position needs to add this paragraph . for example ：()(()), The red one on the left and The green one on the right Is a sequence of two independent valid parentheses . So the state transfer equation is ：dp[i] = dp[i - 1] + 2 + dp[i - dp[i - 1] -2 ].

Icon ： 

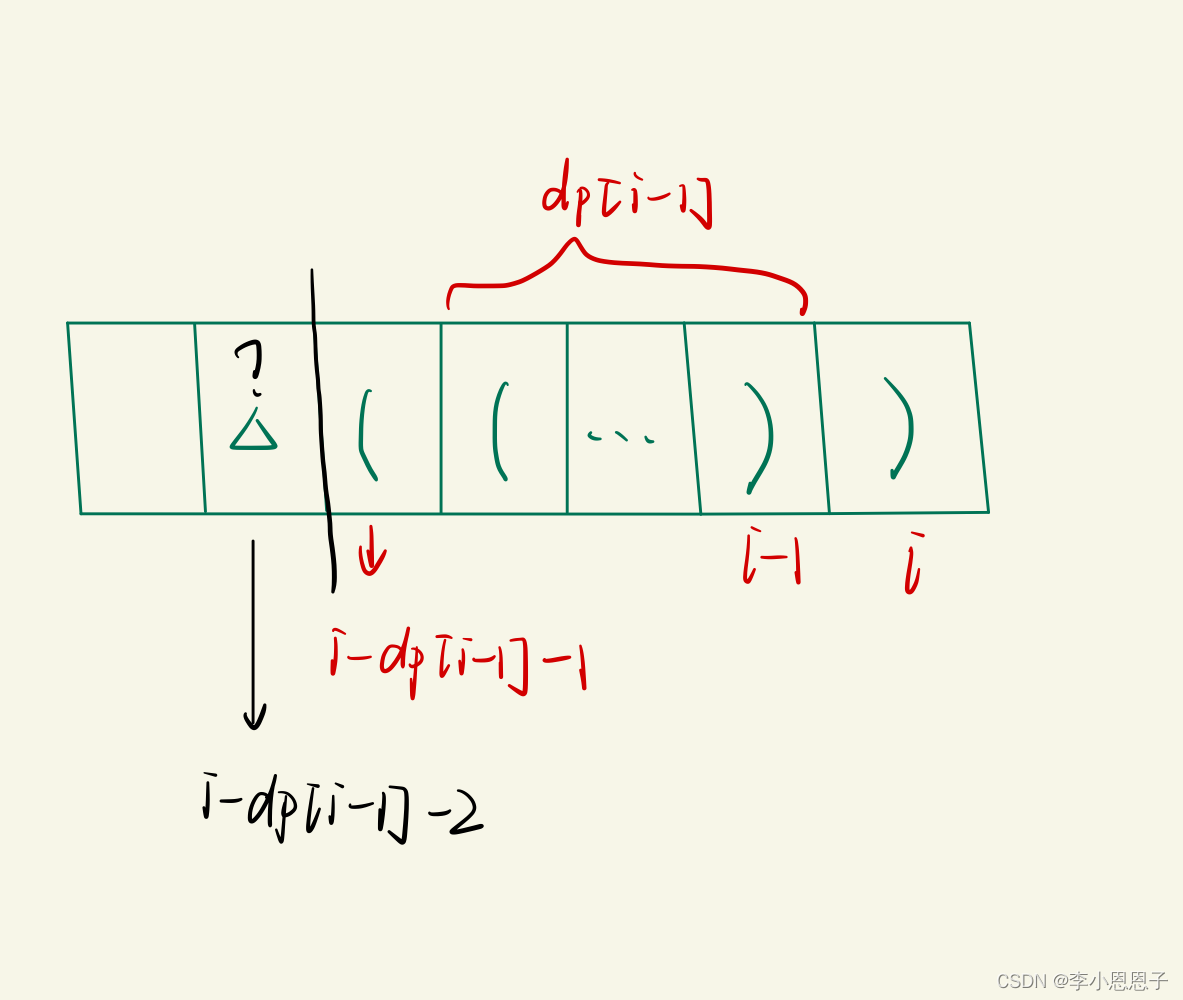
Also note the boundary value , Because we need to use it dp[ i - 2 ], also dp[ i - dp[ i - 1 ] - 2 ], To judge .  

Code ：

class Solution {
    public int longestValidParentheses(String s) {
        // Dynamic programming 
        //dp[i] Denotes the following i The length of the longest valid bracket at the end of the character 
        int res = 0;
        int[] dp = new int[s.length()];
        for(int i = 1;i < s.length();i++){
            if(s.charAt(i) == ')'){
                if(s.charAt(i-1) == '('){
                    if(i >= 2) dp[i] = dp[i - 2] + 2;
                    else dp[i] = 2;
                }else if(i - dp[i - 1] > 0  && s.charAt(i - dp[i - 1] - 1) == '('){
                    if(i - dp[i - 1] >= 2) dp[i] = dp[i - 1] + dp[i - dp[i - 1] - 2] + 2;
                    else dp[i] = dp[i - 1] + 2;
                }
            }
            res = Math.max(res,dp[i]);
        }
        return res;
    }
}

Method 2: look at the analysis , Not good at writing Dynamic Planning , Next time, find an opportunity to practice the topic of Dynamic Planning .