Ml self realization / logistic regression / binary classification

principle

Prediction function ：

• classification ：$0\le h_{\theta }(x)\le 1$
• Tradition ：$h_{\theta }(x)\gg 1||h_{\theta }(x)\ll 0$

Traditional prediction function is transformed into classification prediction function ：

• Traditional prediction function $h_{\theta }(x)$$\stackrel{sigmoid}{*}$ Classification prediction function $h_{\theta }(x)$
  

The process ：
sigmoid:$g(z)=\frac{1}{1+e^{-z}}\stackrel{z=h_{\theta }(x)={\theta }^{T}x}{*}=\frac{1}{1+e^{-{\theta }^{T}x}}$
primary $h_{\theta }(x)=z={\theta }^{T}x={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+...+{\theta }_n{x}_n$
new $h_{\theta }(x)=P(y=1|x;\theta )=\frac{1}{1+e^{-z}}$

Decision boundaries ：

• $new{h}_{\theta }(x)=g(z)\ge 0.5when,recognizebyy=1\Rightarrow z\ge 0\Rightarrow {\theta }^{T}x\ge 0\Rightarrow used{h}_{\theta }(x)\ge 0$
• $new{h}_{\theta }(x)=g(z)\le 0.5when,recognizebyy=0\Rightarrow z\le 0\Rightarrow {\theta }^{T}x\le 0\Rightarrow used{h}_{\theta }(x)\le 0$
• $used{h}_{\theta }(x)=0,Justyes"Strategyedgeworld$

cost function ：
The original cost function ：

• The original cost function cannot be used , Because there are too many local optima
• $J(\theta )=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$,$0\le h_{\theta }(x^{(i)}\le 1$ And $y=0or1$, Lead to the existence of too many local optima , Not a typical convex function
  

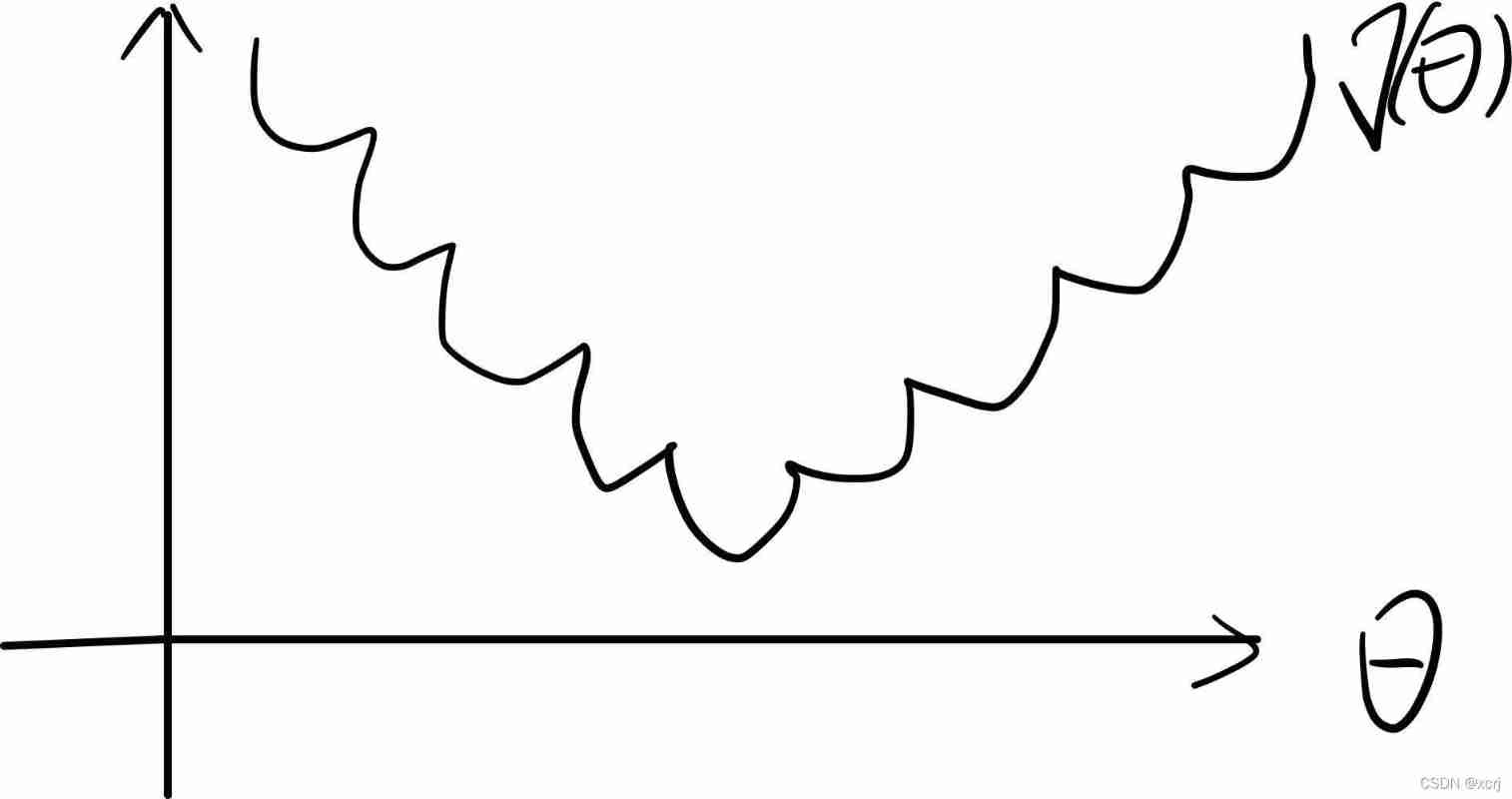
New cost function ： Converse thinking
$$cost(h_{\theta }(x),y)=\{\begin{array}{ll}-\log (h_{\theta }(x))& y=1\\ -\log (1-h_{\theta }(x))& y=0\end{array}$$

Introduce

• l
  $$y=1when\{\begin{array}{l}{h}_{\theta }(x)\to 1\\ Such\; asfruitwant{h}_{\theta }(x)\to 0becost\to +\infty \end{array}$$
• r
  $$y=0when\{\begin{array}{l}{h}_{\theta }(x)\to 0\\ Such\; asfruitwant{h}_{\theta }(x)\to 1becost\to +\infty \end{array}$$

Unified cost function ：

• $cost(h_{\theta }(x),y)=-y\log (h_{\theta }(x))-(1-y)\log (1-h_{\theta }(x))$
• When y=1 when , Keep the front of the above formula 1 part
• When y=0 when , Keep the last of the above formula 1 part

cost function ： Least square method
$$\begin{array}{rl}J(\theta )& =\frac{1}{m}\sum _{i=1}^{m}cost(h_{\theta }(x),y)\\ & =\frac{1}{m}\sum _{i=1}^m[-y\log (h_{\theta }(x))-(1-y)\log (1-h_{\theta }(x))]\end{array}$$

Batch gradient descent algorithm ：

• Repeat until it converges {
  ${\theta }_0:={\theta }_0-\alpha \frac{\partial J(\theta )}{\partial {\theta }_0}$
  ${\theta }_j:={\theta }_j-\alpha \frac{\partial J(\theta )}{\partial {\theta }_j}$
  }
• Repeat until it converges {
  ${\theta }_0:={\theta }_0-\alpha \frac{1}{m}\sum _{i=1}^m[h_{\theta }(x)-y]$
  ${\theta }_j:={\theta }_j-\alpha \frac{1}{m}\sum _{i=1}^m[h_{\theta }(x)-y]x_j$
  }
• Be careful ： Batch gradient descent algorithm needs to update all at the same time ${\theta }_j$

Data sets

Spam differentiation

• Address download spambase.data File can
• Dichotomous problem ：spam or non-spam
• This experiment only takes the first 3 Columns as features , Last 1 Column as the target , Last 1 The column value is 1 when spam, Last 1 The column value is 0 when non-spam,

Code

from mpl_toolkits.mplot3d import Axes3D
import pandas as pd
import numpy as np
import matplotlib
import matplotlib.pyplot as plt

matplotlib.rcParams['font.family'] = 'STSong'
matplotlib.rcParams['font.size'] = 20


class DataSet(object):
    """ X_train  Training set samples  y_train  Training set sample value  X_test  Test set samples  y_test  Test set sample values  """

    def __init__(self, X_train, y_train, X_test, y_test):
        self.X_train = X_train
        self.y_train = y_train
        self.X_test = X_test
        self.y_test = y_test


class LogisticRegression(object):
    """  Logical regression  """

    def __init__(self, n_feature):
        self.theta0 = 0
        self.theta = np.zeros((n_feature, 1))

    def sigmoid(self, z):
        return 1 / (1 + np.exp(-z))

    def gradient_descent(self, X, y, alpha=0.001, num_iter=100):
        costs = []
        m, _ = X.shape
        for i in range(num_iter):
            #  Predictive value 
            h = self.sigmoid(np.dot(X, self.theta) + self.theta0)
            #  cost function 
            cost = (1 / m) * np.sum(-y * np.log(h) - (1 - y) * (np.log(1 - h)))
            costs.append(cost)
            #  gradient 
            dJ_dtheta0 = (1 / m) * np.sum(h - y)
            dJ_dtheta = (1 / m) * np.dot((h - y).T, X).T
            #  Update all at the same time theta
            self.theta0 = self.theta0 - alpha * dJ_dtheta0
            self.theta = self.theta - alpha * dJ_dtheta

        return costs

    def show_train(self, costs, num_iter):
        """  Show the training process  """
        fig = plt.figure(figsize=(10, 6))
        plt.plot(np.arange(num_iter), costs)
        plt.title(" Cost changes ")
        plt.xlabel(" The number of iterations ")
        plt.ylabel(" cost ")
        plt.show()

    def hypothesis(self, X, theta0, theta):
        """  Prediction function  """
        h0 = self.sigmoid(self.theta0 + np.dot(X, self.theta))
        h = [1 if elem > 0.5 else 0 for elem in h0]
        return np.array(h)[:, np.newaxis]


def read_data():
    """  Reading data  """
    # names： Header 
    # sep： Separator 
    # skipinitialspace： Ignore the space after the delimiter 
    # comment： Ignore \t Note after 
    # na_values： Use ? Replace NA Value 
    origin_data = pd.read_csv("./data/spambase.data", sep=",", skipinitialspace=True, comment="\t", na_values="?")
    data = origin_data.copy()
    # tail() Print last n Row data 
    print(data.tail())
    return data


def clean_data(data):
    """  Data cleaning ： Handling outliers  """
    # dataset Does it contain NA data 
    # pandas 0.22.0+ Only then isna(), Upgrade order ：pip install --upgrade pandas==0.22.0
    print('NA Row number ：', data.isna().sum())
    #  Delete the exception line 
    cleaned_data = data.dropna()
    return cleaned_data


def show_data(data):
    """  Show the data  """
    count_spam = 0
    count_non_spam = 0
    for c in data.iloc[:, -1]:
        if c == 1:
            count_spam += 1
        else:
            count_non_spam += 1

    print(" Number of spam ：", count_spam)
    print(" Number of normal mail ：", count_non_spam)


def split_data(data):
    """  Divide the data   Divided into train, test;train Used to train the prediction function ,test Used to test the generalization ability of the predicted function value  """
    copied_data = data.copy()
    # frac： The proportion of rows extracted ;random_state  Random seeds 
    train_dataset = copied_data.sample(frac=0.8, random_state=1)
    #  Take the rest of the test set 
    test_dataset = copied_data.drop(train_dataset.index)

    X_train = train_dataset.iloc[:, 0:3]
    y_train = train_dataset.iloc[:, -1]
    X_test = test_dataset.iloc[:, 0:3]
    y_test = test_dataset.iloc[:, -1]
    dataset = DataSet(X_train, y_train, X_test, y_test)

    return dataset


def evaluate_model(y_test, h):
    """  Evaluation model  """
    # MSE： Mean square error 
    print("MSE: %f" % (np.sum((h - y_test) ** 2) / len(y_test)))
    # RMSE： Root mean square difference 
    print("RMSE: %f" % (np.sqrt(np.sum((h - y_test) ** 2) / len(y_test))))

def show_result(X_test, y_test, h):
    # figure canvas 
    fig = plt.figure(figsize=(16, 8), facecolor='w')
    # subplot Subgraphs 
    plt.subplots_adjust(left=0.05, right=0.95, bottom=0.05, top=0.9)

    # 221：nrows=2, ncols=2, index=1
    ax = fig.add_subplot(121, projection='3d')
    ax.set_title("y_test")
    ax.set_xlabel('Feature 1')
    ax.set_ylabel('Feature 2')
    ax.set_zlabel('Feature 3')
    # x,y,z,c(color),marker( shape )
    ax.scatter(X_test[:, 0], X_test[:, 1], X_test[:, 2], c=y_test, marker='o')
    plt.grid(True)

    ax1 = fig.add_subplot(122, projection='3d')
    ax1.set_title("h")
    ax1.set_xlabel('Feature 1')
    ax1.set_ylabel('Feature 2')
    ax1.set_zlabel('Feature 3')
    # x,y,z,c(color),marker( shape )
    ax1.scatter(X_test[:, 0], X_test[:, 1], X_test[:, 2], c=h, marker='*')
    plt.grid(True)

    plt.show()

def main():
    #  Reading data 
    data = read_data()
    #  Data cleaning 
    cleaned_data = clean_data(data)
    #  Mean normalization , Before the data set used 3 There is little difference in the range of column data , Do not normalize the mean 
    #  Display data 
    show_data(cleaned_data)
    #  Split data 
    dataset = split_data(cleaned_data)
    #  Build the model 
    _, n = dataset.X_train.shape
    logistic_regression = LogisticRegression(n)
    num_iteration = 300
    costs = logistic_regression.gradient_descent(dataset.X_train, dataset.y_train.values[:, np.newaxis], alpha=0.5,
                                                 num_iter=num_iteration)
    #  Show the training process 
    logistic_regression.show_train(costs, num_iteration)
    #  Evaluation model 
    h = logistic_regression.hypothesis(dataset.X_test, logistic_regression.theta0, logistic_regression.theta)
    evaluate_model(dataset.y_test.values[:, np.newaxis], h)
    #  Display the results 
    show_result(dataset.X_test.values,dataset.y_test.values, h.ravel())


if __name__ == '__main__':
    main()