[unique] what is the [chain storage structure]?

3.6 Chain storage structure for linear tables 🪢

3.6.1. The solution to the shortage of sequential storage structure

Sequential storage of linear tables

The sequential storage structure of linear tables has its disadvantages , The biggest disadvantage is that a large number of elements need to be moved during insertion and deletion , This obviously takes time . Can you find a way to solve it ？

To solve this problem , We have to consider the causes of this problem ：

Why when inserting and deleting , You have to move a lot of elements , After careful analysis , The reason for the discovery is that the storage locations of two adjacent elements also have a neighbor relationship . They are numbered 1,2,3,…,n, They are also located next to each other in memory , There is no gap in the middle , Of course, you can't get involved quickly , And after deletion , There will be a gap , Nature needs to make up for . Here's the problem .

Idea one 🧐： Leave an empty position between each element , So when you want to insert , It will not move . But how can an empty location solve the problem of inserting data in multiple identical locations ？ So this idea obviously doesn't work .

Idea 2 🧐： Then leave enough space between each element , Determine the gap size according to the actual situation , such as 10 individual , When inserting like this , There is no need to move . In case 10 We have run out of seats , Then consider moving so that there is... Between each position 10 Empty space . If you remove , Just delete , Leave the position blank . This seems to temporarily solve the problem of inserting and deleting mobile data . But this is for more than 10 Insertion of data in the same location , There are still problems in efficiency . For data traversal , It will also waste judgment time because there are too many empty positions . And obviously the space complexity here has increased , Because there are several empty positions between each element .

Idea three ： We have to leave enough room between adjacent elements anyway , Then simply don't consider the adjacent position of all elements , Go wherever there is a vacant seat , Just let each element know where its next element is , such , We can use the first element , You know the location of the second element （ Memory address ）, And find it ; In the second element , Find the location of the third element （ Memory address ）. In this way, we can find all the elements through traversal .

Obvious , The third idea is the main line of our discussion today .

3.6.2. Linear watch chain storage structure definition

First map ：

The linear table Chain storage structure It is characterized by using a set of arbitrary storage units to store the data elements of the linear table , This set of storage units can be continuous , It could be discontinuous . That means , These data elements can exist anywhere in memory that is not occupied .

In a sequential structure , Each data element only needs to store data element information . Now in the chain structure , In addition to storing data elements , Also store the storage address of its subsequent elements . therefore , For data elements ai Come on , In addition to storing its own information , It also needs to store a message indicating its direct successor （ That is, the direct storage location ）. We call the domain in which data element information is stored Data fields , The domain in which the direct successor location is stored is called Pointer to the domain . The information stored in a pointer field is called a pointer or chain . These two parts of information make up the data elements ai The storage image of , be called node （Node）.

n Links of nodes form a linked list , That is, the linear table （a1,a2, … ,an） The chain storage structure of , Because each node of this linked list contains only one pointer field , So it's called a single linked list . Single chain list The data elements of the linear table are formally linked together in their logical order through the pointer field of each node , Pictured ：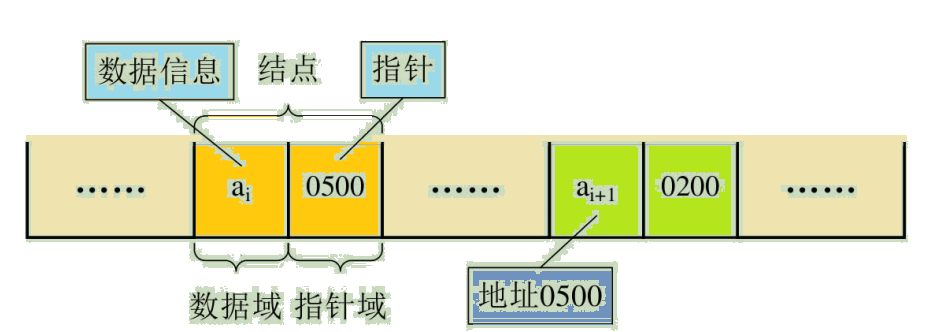

For linear tables , There has to be a head and a tail , Linked lists are no exception . We call the storage location of the first node in the linked list The head pointer , Then the access of the whole linked list must start from the pointer . Every node after , In fact, it is the position pointed by the subsequent pointer of the previous . The last node pointer of the linear linked list is “ empty ”（ Usually use NULL or ^ Express ）.

Sometimes , In order to operate the linked list more conveniently , A node will be attached before the first node of the single linked list , be called Head node . The data field of the header node can store no information , Additional information such as the length of the linear table can also be stored , The pointer field of the head node stores the pointer to the first node , Pictured ：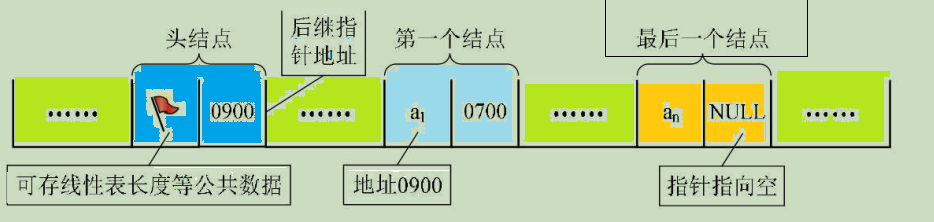

3.6.3 Similarities and differences between head pointer and head node

It is also a header pointer and a header node , What is all this , take it easy ！ Look at the picture ：

This time , I see! , Hey , Let's keep on learning ~~

3.6.4. Linear watch chain storage structure code description

If the linear table is empty , The pointer field of the header node is null , Pictured ：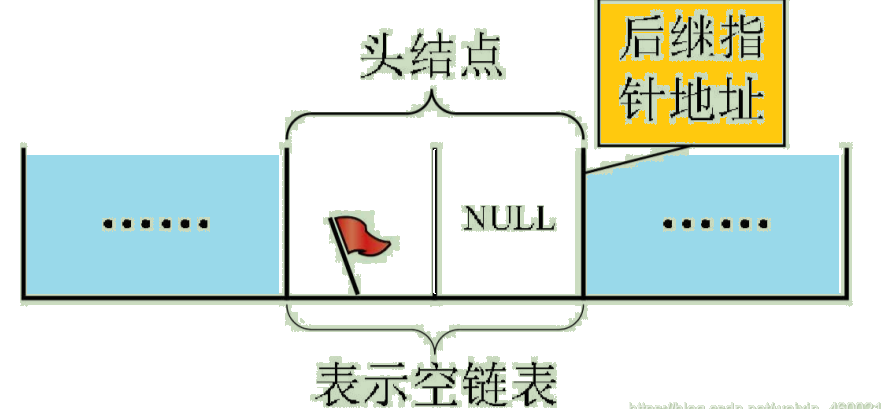

Next, let's take a look at the diagram of the general single linked list ：
Insert picture description here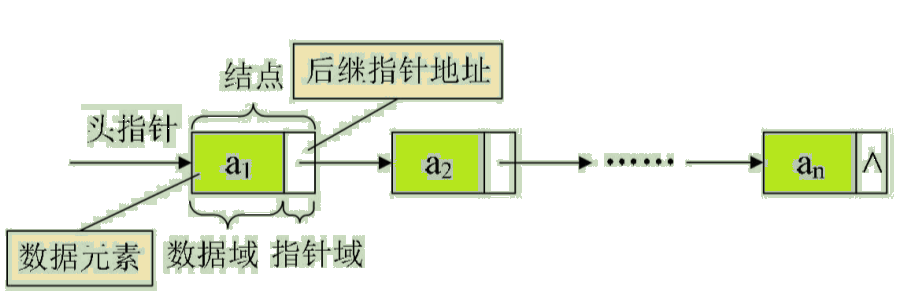

Use the code to represent the single linked list ：

/*  Single linked list storage structure of linear table  */
typedef struct Node
{
    
	/*  Data fields  */
	ELemType data;
	/*  Pointer to the domain  */
	struct Node *next;
} Node;
/*  Definition LinkList */
typedef struct Node *LinkList;

From this structural definition , We know , A node consists of a data field for storing data elements and a pointer field for storing subsequent node addresses . hypothesis p It points to the second line of the linear table i Pointers to elements , Then the node ai We can use p->data To express ,p->data The value of is a data element , node ai The pointer field of can be used p->next To express ,p->next The value of is a pointer .p->next To whom ？ Of course, it points to the third i+1 Elements , Point to ai+1 The pointer to . in other words , If p->data = ai, that p->next->data = ai+1, See figure ：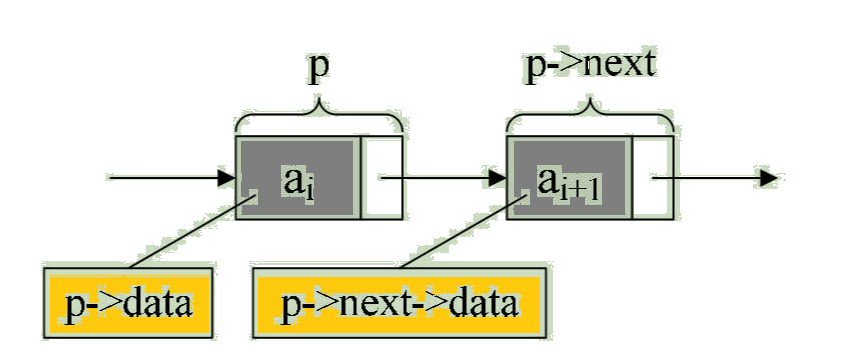

1. Read single linked list

In the sequential storage structure of a linear table , It's easy for us to calculate the storage location of any element . But in a single linked list , Due to the first i There is no way to know from the beginning , You have to start from scratch .

Get the... Of the linked list i A data algorithm ：

Declare a pointer p Point to the first node in the list , initialization j from 1 Start ;
When j < i when , Just traverse the linked list , Give Way p The pointer moves backward , Keep pointing to the next node ,j Add up 1;
If you go to the end of the list p It's empty , That means i The nodes do not exist ;
Otherwise, the search is successful , Return node p The data of .

/*  Initial conditions ： Sequential linear table  L  Already exist ,1 <= i <= ListLength(L) */
/*  Operating results ： use  e  return  L  pass the civil examinations  i  Values of data elements  */
Status GetElem(LinkList L, int i, ElemType *e)
{
    
	int j;
	LinkList p;		/*  Declare a pointer  p */
	p = L->next;	/*  Give Way  p  Point to the list  L  The first node of ( If there is a header node, it refers to the header node ) */
	j = 1;			/* j  For counter  */
	/* p  Not null and counter  j  Not yet equal to  i  when , The cycle continues  */
	while (p && j < i)
	{
    
		p = p->next;	/*  Give Way  p  Point to the next node  */
		++j;
	}
	if (!p || j > i) 
		return ERROE	/*  The first  i  The nodes do not exist  */
	*e = p->data;		/*  Take the first place  i  Data of nodes  */
	return OK;
}

To put it bluntly , Is to start from scratch , Until the first i It's a node . Because the time complexity of this algorithm depends on i The location of , When i = 1 when , There is no need to traverse , When i = n When I do, I traverse n - 1 The next time . So the worst-case time complexity is O(n).

Because there is no table length defined in the structure of a single linked table , So you can't know how many times to cycle in advance , Therefore, it is inconvenient to use for To control the cycle . Its main core idea is “ The working pointer moves back ”, This is actually a common technology of many algorithms .

2. Insertion of single chain table

Suppose the storage element e The node of is s, To implement a node p 、p->next and s Changes in the logical relationship between , Just put the node s Insert to node p and p->next Between . Pictured ：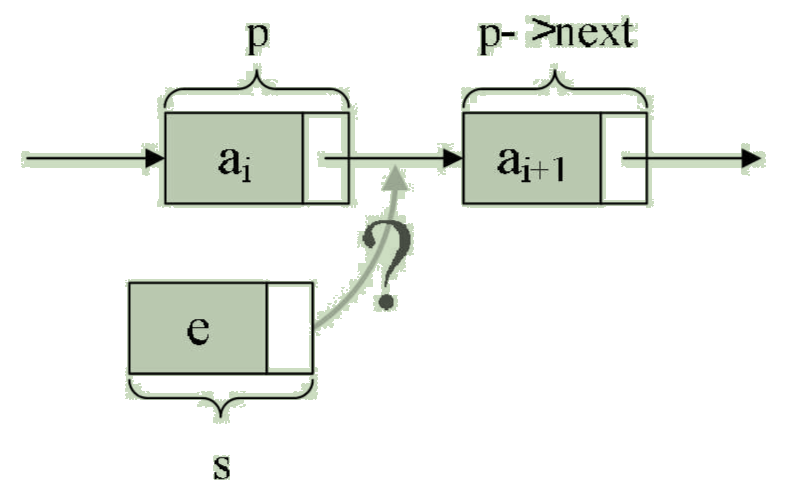

You can find , Just let s->next and p->next Just make a little change to the pointer of .

s->next = p->next;		/*  Give Way p The successor node of is changed to s The successor node of  */
p->next = s;			/*  Put the node s become p The successor node of  */

The law of triplicate ：

The order of two sentences cannot be exchanged ！
The order of two sentences cannot be exchanged ！
The order of two sentences cannot be exchanged ！

Then let's see why we can't exchange ：
If first p->next=s; Again s->next=p->next; What will happen? ？ ha-ha , Because the first sentence will make p->next Cover it with s The address of the . that s->next=p->next, In fact, it is equal to s->next=s. So really have ai+1 The node of the data element has no superior . Such an insert operation is a failure , It caused the embarrassing situation of dropping the chain on the spot .

When inserted correctly, it looks like this . Pictured ：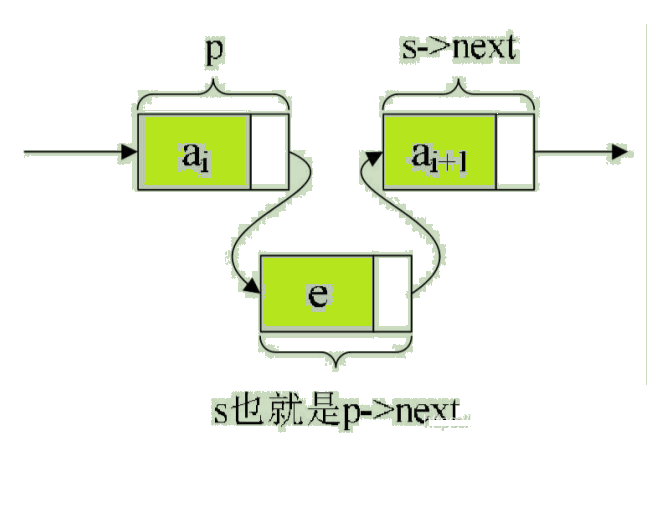

Single linked list No i The algorithm idea of a data insertion node ：

1. Declare a pointer p Point to the chain header node , initialization j from 1 Start ;
2. When j < i when , Just traverse the linked list , Give Way p The pointer moves backward , Keep pointing to the next node ,j Add up 1;
3. If you go to the end of the list p It's empty , That means i The nodes do not exist ;
4. Otherwise, the search is successful , Generate an empty node in the system s;
5. Put data elements e Assign a value to s->data;
6. Insert standard statement of single linked list s->next = p->next; p->next = s;
7. Return to success .

The algorithm code is as follows ：

/*  Initial conditions ： Sequential linear table  L  Already exist ,1 <= i <= ListLength(L) */
/*  Operating results ： stay  L  pass the civil examinations  i  Insert a new data element before the node location  e,L  Increase the length of  1 */
Status ListInsert(LinkList *L, int i, ElemType e)
{
    
	int j;
	LinkList p, s;
	p = *L;
	j = 1;
	/*  Search for the first  i-1  Nodes  */
	while (p && j < i)
	{
    
		p = p->next;
		++j;
	}
	/*  The first  i  The nodes do not exist  */
	if (!p || j > i)
		return ERROR;
	/*  Generate new nodes (C Standard functions ) */
	s = (LinkList)malloc(sizeof(Node));
	s->data = e;
	/*  take  p  The successor node of is assigned to  s  In the subsequent  */
	s->next = p->next;
	/*  take  s  Assign a value to  p  In the subsequent  */
	p->next = s;
	return OK;
}

malloc : C Language standard functions , Its function is to generate a new node , Its type and Node It's the same , In fact, the essence is to find a small space in the memory , Ready to store data e Of s node .

3. Deletion of single chain table

Set storage element ai The node of is q, To realize the node q Delete single linked list , In fact, it points its predecessor node directly to its successor node . Pictured ：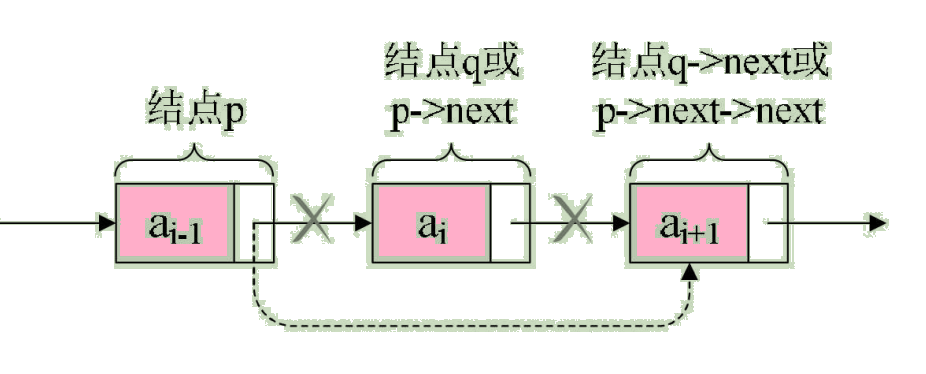

All we have to do , It's actually one step ,p->next=p->next->next, use q To replace p->next, That is ：
q=p->next; p->next=q->next;

Single linked list No i An algorithm idea of deleting data nodes ：

1. Declare a pointer p Point to the chain header node , initialization j from 1 Start ;
2. When j < i when , Just traverse the linked list , Give Way p The pointer moves backward , Keep pointing to the next node ,j Add up 1;
3. If you go to the end of the list p It's empty , That means i The nodes do not exist ;
4. Otherwise, the search is successful , Delete the node to be deleted p->next Assign a value to q;
5. Delete standard statement of single linked list p->next = q->next;
6. take q The data in the node is assigned to e, As a return ;
7. Release q node ;
8. Return to success .

The algorithm code is as follows ：

/*  Initial conditions ： Sequential linear table  L  Already exist ,1 <= i <= ListLength(L) */
/*  Operating results ： stay  L  pass the civil examinations  i  Insert a new data element before the node location  e,L  Increase the length of  1 */
Status ListInsert(LinkList *L, int i, ElemType e)
{
    
	int j;
	LinkList p, q;
	p = *L;
	j = 1;
	/*  Traversal search  i - 1  Nodes  */
	while (p->next && j < i)
	{
    
		p = p-> next;
		++j;
	}
	/*  The first  i  The nodes do not exist  */
	if (!(p->next) || j > i)
		return ERROR;
	q = p->next;
	/*  take  q  The successor of is assigned to  p  In the subsequent  */
	p->next = q->next;
	/*  take  q  The data in the node is given to  e */
	*e = q->data;
	/*  Let the system recycle this node , Free memory  */
	free(q)
	return OK;
}

free : The function is to let the system recycle a Node node , Free memory .

Analyze the above single linked list insertion and deletion algorithm , We found that , They are actually composed of two parts ： The first part is to traverse and find i Nodes ; The second part is to insert and delete nodes .

In terms of the whole algorithm , We can easily deduce ： Their time complexity is O(n). If we don't know the second time i Pointer position of a node , Single linked list data structure in the insert and delete operations , Compared with the linear table, the sequential storage structure has no great advantage . But if , We hope to start from i A place , Insert 10 Nodes , For a sequential storage structure, it means , Every insert needs to be moved n-i Nodes , Every time O(n). And the single linked list , We just need to do it the first time , Find No i A pointer to a position , This is the case O(n), The next step is simply to move the pointer by assignment , The time complexity is zero O(1). obviously , The more frequently you insert or delete data , The more obvious the efficiency advantage of single linked list .

---

4. The whole table of a single linked table is created

Creation of sequential storage structure , In fact, it is the initialization of an array , That is, the process of declaring an array of types and sizes and assigning values . The single linked list and the sequential storage structure are different . For each linked list , The size and location of the space it occupies do not need to be allocated in advance , It can be generated in real time according to the system situation and actual needs .

The process of creating a single linked list is a process of dynamically generating a linked list . From “ Empty table ” From the initial state of , Establish each element node in turn , And insert the linked list one by one .

The algorithm idea of creating a single linked table and an entire table ：

1. Declare a pointer p And counter variables i;
2. Initialize an empty linked list L;
3. Give Way L The pointer to the head node of points to NULL, That is to establish a single linked list of leading nodes ;
4. loop ：
Generate a new node and assign it to p;
Randomly generate a number and assign it to p The data field of p->data;
take p Insert between the head node and the previous new node .

The algorithm code is as follows ：

/*  Randomly generated  n  The value of the elements , Establish a single chain linear table with header nodes  L( The first interpolation ) */
void CreateListHead(LinkList *L, int n)
{
    
	LinkList p;
	int i;
	/*  Initialize random number seed  */
	srand(time(0));
	*L = (LinkList)malloc(sizeof(Node));
	/*  First create a single linked list of the leading nodes  */
	(*L)->next = NULL;
	for (i = 0; i < n; i++)
	{
    
		/*  Generate new nodes  */
		p = (LinkList)malloc(sizeof(Node));
		/*  Random generation  100  Numbers within  */
		p->data = rand() % 100 + 1;
		p->next = (*L)->next;
		/*  Insert into the header  */
		(*L)->next = p;
	}
}

In this algorithm code , We actually cut in line , Is to always keep the new node in the first position . I can also abbreviate this algorithm to head interpolation , Pictured ：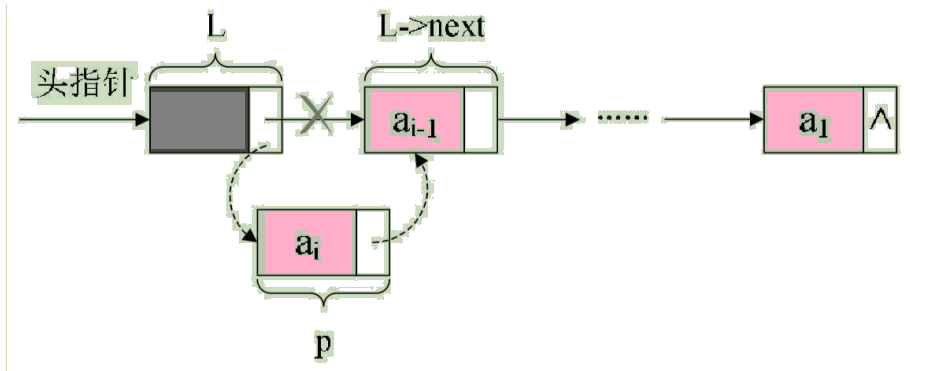

We can also create a single linked list in another way , Let's start with the implementation code ：

/*  Randomly generated  n  The value of the elements , Establish a single chain linear table with header nodes  L( The tail interpolation ) */
void CreateListTail(LinkList *L, int n)
{
    
	LinkList p, r;
	int i;
	/*  Initialize random number seed  */
	srand(time(0));
	/*  For the entire linear table  */
	*L = (LinkList)malloc(sizeof(Node));
	/* r  Is the node pointing to the tail  */
	r = *L;
	for (i = 0; i < n; i++)
	{
    
		/*  Generate new nodes  */
		p = (Node *)malloc(sizeof(Node));
		/*  Random generation  100  Numbers within  */
		p->data = rand() % 100 + 1;
		/*  Point the pointer of the terminal node at the end of the table to the new node  */
		r->next = p;
		/*  Define the current new node as the footer terminal node  */
		r = p;
	}
	/*  Indicates the end of the current linked list  */
	r-> = NULL;
}	

Be careful L And r The relationship between ,L It refers to the whole single linked list , and r Is a variable pointing to the tail node ,r Will change with the cycle , and L As the cycle grows into a multi node linked list .

---

5. Delete the whole table of the single linked list

The algorithm idea of deleting a single linked list and the whole table is as follows ：

1. Declare a pointer p and q;
2. Assign the first node to p;
3. loop ：
Assign the next node to q;
Release p;
take q Assign a value to p.

The algorithm implementation code is as follows ：

/*  Initial conditions ： Sequential linear table  L  Already exists , Operating results ： take  L  Reset to empty table  */
Status ClearList(LinkList *L)
{
    
	LinkList p, q;
	/* p  Point to the first node  */
	p = (*L)->next;
	/*  Not to the end of the watch  */
	while (p)
	{
    
		q = p->next;
		free(p);
		p = q;
	}
	/*  The header node pointer field is null  */
	(*L)->next = NULL;
	return OK;
}

Be careful ： Why should there be one in the code q There is , direct free§, then p = p->next ; No, that's fine , Here we need to know p Point to a node , It has data fields , And pointer fields . Doing it free§ When , It is to delete the entire node and release the memory .

---

3.6.5 Advantages and disadvantages of single linked list structure and sequential storage structure

Don't talk much , Upper figure ：

1. Circular linked list

Change the pointer end of the terminal node in the single linked list from a null pointer to a head node , So that the whole single list forms a ring , This kind of single linked list with head and tail is called single loop linked list , It's called circular list for short （circular linked list）.

Circular linked list can start from any node , Access to all nodes of the linked list .

In order to make the processing of empty linked list consistent with that of non empty linked list , We usually set a header node , Of course , That's not to say , Circular linked list must have a header node , This requires attention . The empty linked list with a head node in the circular linked list is shown in the figure ：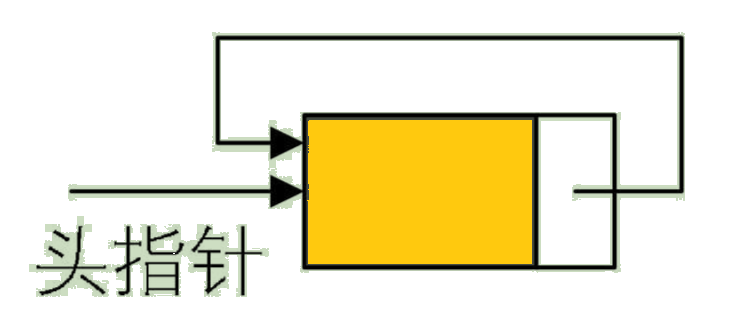

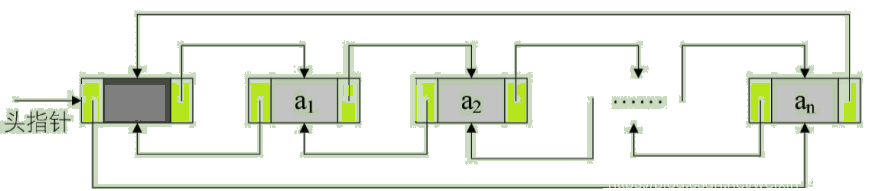
For the non empty circular linked list, it is shown in Figure ：

The main difference between circular linked list and single linked list lies in the judgment conditions of the cycle , It's judgment p->next Is it empty , Now it is
p->next Not equal to header node , Then the cycle is not over .

In a single chain table , When we have the head node , We can use O(1) Time to access the first node , But for the last node to access , But I need O(n) Time , Because we need to scan all the single linked lists .

Is it possible to use O(1) The time from the linked list pointer to the last node ？ Certainly. .

But we need to modify the circular linked list , No head pointer , Instead, the tail pointer to the terminal node is used to represent the circular linked list , At this point, it is very convenient to find the start node and the end node . Pictured ：

As you can see from the above figure , Tail pointer for terminal node rear instructions , Then the search terminal node is O(1), And start , In fact, that is rear->next->next, The time complexity is also O(1).

Take an example of a program , When you want to merge two circular linked lists into one table , With the tail pointer, it's very simple . For example, the following two circular linked lists , Their tail pointers are rearA and rearB, Pictured ：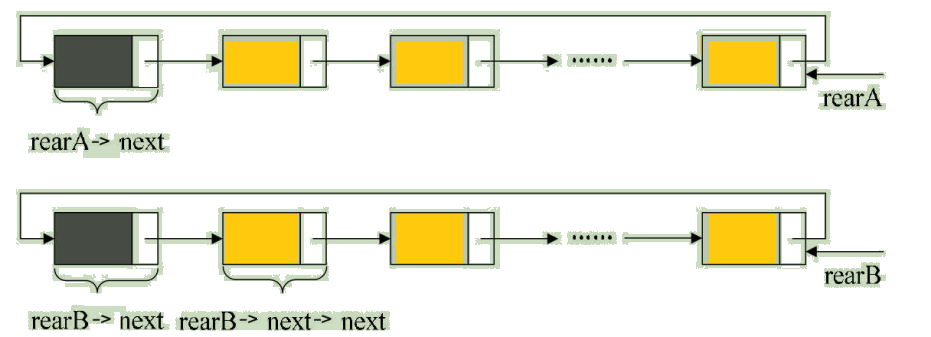

To merge them , Just do the following , Pictured ：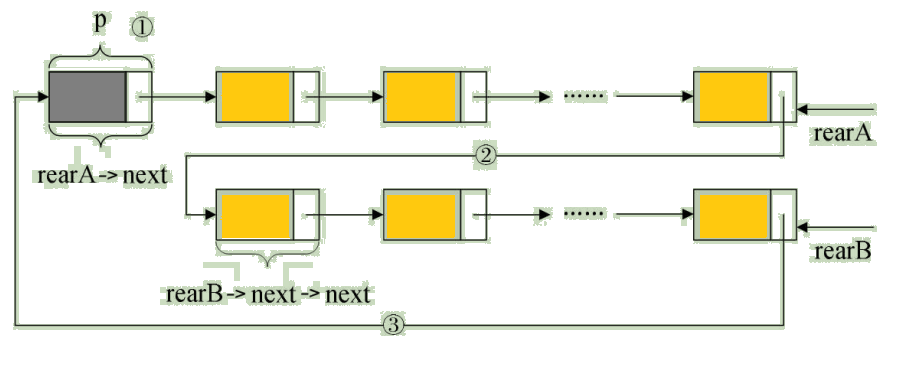

Just saying but not writing fake moves , The code is as follows ：

/*  preservation  A  Table header , namely  ① */
p = rearA->next;
/*  Point to  B  The first node of the table （ It's not the head node ） Assign a value to  RearA->next, namely  ② */
rearA->next = rearB->next->next;
q = rearB->next;
/*  The original  A  The head node of the table is assigned to  rearB->next, namely  ③ */
rearB->next = p;
/*  Release  q */
free(q);

2. Double linked list

Our single linked list , Always find nodes from beginning to end , Isn't it possible to traverse both forward and backward ？ Certainly. , Just need to add something .

We are in the single linked list , With next The pointer , This makes the time complexity of finding the next node to be O(1). But if we are looking for the previous node , The worst time complexity is O(n) 了 , Because we have to go through the search from the beginning every time .

In order to overcome the disadvantage of unidirectionality , Our old scientists , Designed a two-way linked list . Double linked list （double linkedlist） Is in each node of the single linked list , Set another one to point to it Precursor node A pointer to the domain . Therefore, the nodes in the two-way linked list have two pointer fields , A pointer to a Direct follow-up , The other points directly to the precursor .

/*  Two way linked list storage structure of linear table  */
typedef struct DulNode{
        
	ElemType data;    
	struct DuLNode *prior;    /*  Direct precursor pointer  */    
	struct DuLNode *next;     /*  Direct successor pointer  */
} DulNode, *DuLinkList;

Since a single linked list can also have a circular linked list , Of course, a two-way linked list can also be a circular list . The empty linked list of the loop leading node of the bidirectional linked list is shown in the figure :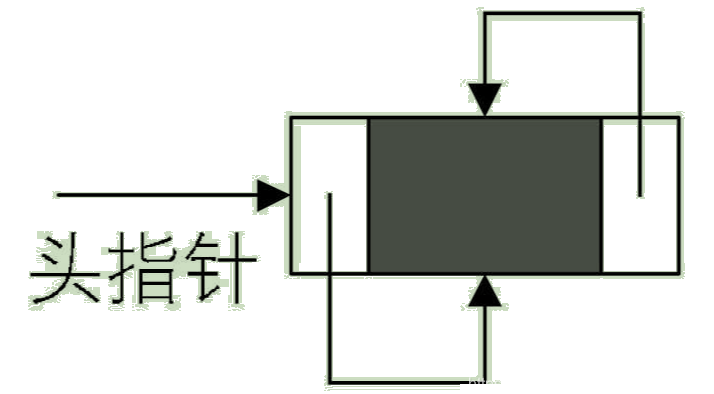

The two-way linked list of the leading node of the non empty loop is shown in the figure ：

Because this is 【 Double linked list 】, So for a node in the linked list p, its The next precursor and its The successor of the precursor Nature is itself , namely ：

p->next->prior = p = p->prior->next

A two-way linked list is an extended structure from a single linked list , So many of its operations are the same as those of the single linked list , For example, find the length of ListLength, Look up the GetElem, Get the position of the element LocateElem etc. , These operations only involve a pointer in one direction , Another pointer is too many to help .

Just like life , If you want to have fun, you have to work hard first , If you want to harvest, you have to pay a price . Since the two-way linked list is more than the single linked list, such as data structures such as reverse traversal and search , Then you need to pay a small price ： When inserting and deleting , Two pointer variables need to be changed .

When inserting , It's not complicated , But order is important , Never write it backwards .

Let's now assume that the storage element e The node of is s, To realize the node s Insert to node p and p->next The following steps are needed between , Pictured ：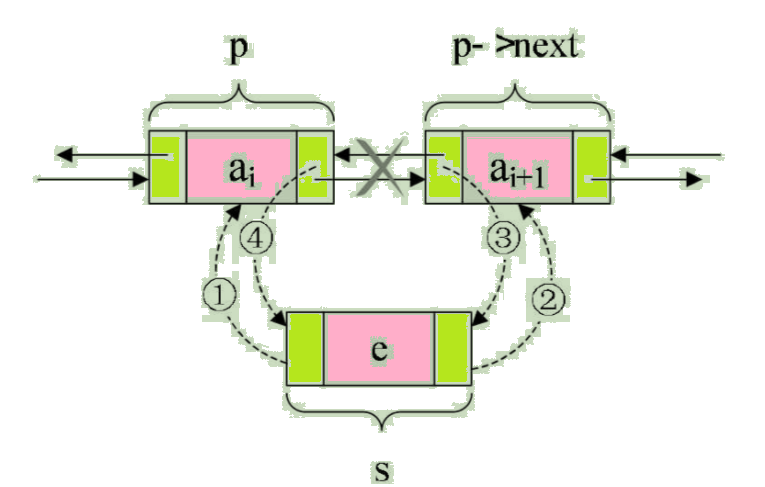

Steps are as follows ：

/*  hold  p  Assign a value to  s  The precursor of , As shown in figure,  ① */
s->prior = p;
/*  hold p->next Assign a value to s In the subsequent , As shown in figure,  ② */
s->next = p->next; 
/*  hold s Assign a value to p->next The precursor of , As shown in figure, ③ */
p->next->prior = s; 
/*  hold s Assign a value to p In the subsequent , As shown in figure, ④ */
p->next = s;

The key is their order , Due to the first 2 And the first step 3 All the steps are used p->next. If the first 4 Step first , Will make p->next It turns into s, So that the inserted work cannot be completed . So we might as well remember the above picture on the basis of understanding , The order is to get it done first s The precursor and successor of , The precursor of the node after finishing , Finally, we solve the following problem of the previous node .

If the insert operation is understood , Then delete , It's simpler .

To delete a node p, Just the next two steps , Pictured :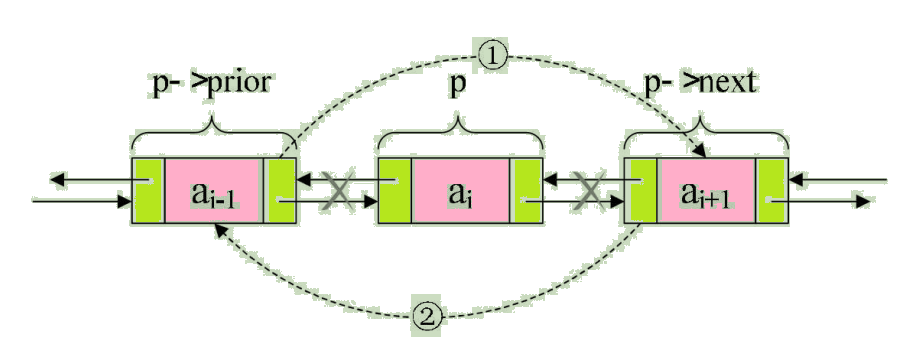

Steps are as follows ：

/*  hold p->next Assign a value to p->prior In the subsequent , As shown in figure, ① */
p->prior->next = p->next;
/*  hold p->prior Assign a value to p->next The precursor of , As shown in figure, ② */
p->next->prior = p->prior;
/*  Release nodes  */
free(p); 

A double linked list is relative to a single linked list , More complicated , After all, it has more prior The pointer , For insertion and deletion , You need to be extra careful . In addition, because each node needs to record two pointers , So it takes up a little more space . however , Because of its good symmetry , Make the operation of the front and back nodes of a node , Bring convenience , It can effectively improve the time performance of the algorithm . To put it bluntly , Is to trade space for time .

3. Static list ️

C Language has the powerful function of pointer , It is also the first choice for many people in the computer field to describe the data structure C One of the reasons for language . The pointer can make C It is very easy to manipulate the address and data in memory , This is more flexible and convenient than other high-level languages .Java、C# And so on , Although no pointer is used , But because objects are enabled Reference mechanism , From a certain angle, it also indirectly realizes some functions of the pointer . But for other languages , Such as Basic、Fortran And other early programming languages are not so convenient for the operation of some data structures .

Some predecessors came up with the idea of using arrays instead of pointers , Describe the single linked list ： First, let the elements of the array be composed of two data fields ,data and cur. in other words , Each subscript of the array corresponds to a data And a cur. Data fields data, Used to store data elements , That is, the data we usually need to process ; and cur It's equivalent to next The pointer , The subscript that holds the subsequent of the element in the array , We put cur be called The cursor .

We call this kind of linked list described by array static linked list , This method of description is also called Cursor implementation method .

For our convenience, insert data , You usually make the array larger , So that some free space can be inserted without overflow .

Describe it in code ：

/*  Static linked list storage structure of linear list  */
/*  Suppose the maximum length of the linked list is 1000 */
#define MAXSIZE 1000
typedef struct
{
        
	ElemType data;    
	/*  The cursor （Cursor）, by 0 When, it means no direction  */    
	int cur;                             
} Component,   
StaticLinkList[MAXSIZE]; 

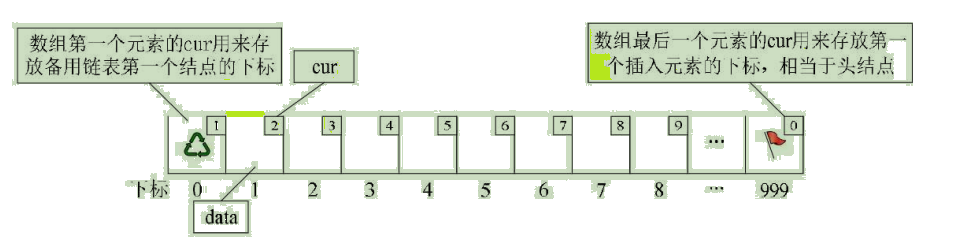
Treat the first and last elements of the array as special elements , No data . We usually call the unused array elements as standby linked list . And the first element of the array , That is, the subscript is 0 The elements of the cur Just store the subscript of the first node of the standby list ; And the last element of the array cur The subscript of the first element with a value is stored , It is equivalent to the function of the head node in the single linked list , When the whole linked list is empty , Then for 0. Pictured ：

Suppose we have stored the data in the static linked list , For example, they are stored separately “ nail ”、“ B ”、“ Ding ”、“ E ”、“ Oneself ”、“ Geng ” Data such as , Then its status is as shown in the figure ：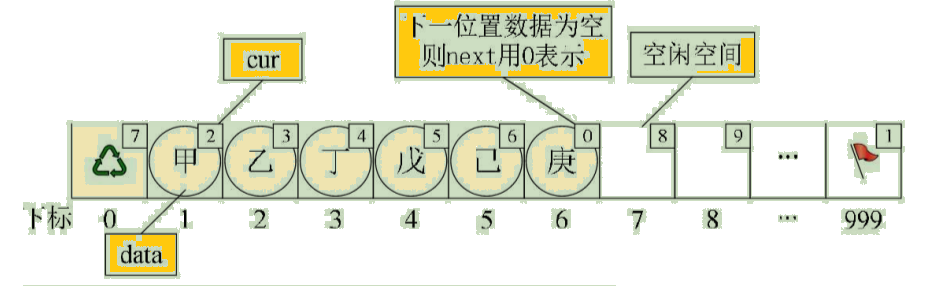
here “ nail ” There is the next element “ B ” The cursor of 2,“ B ” Then there is the next element “ Ding ” The subscript 3. and “ Geng ” Is the last value element , So it's cur Set to 0. And the last element cur Causation “ nail ” Is the first value element and the subscript that holds it is 1. The first element is subscripted as 7, So it's cur come into being 7.

(1) Static list insert operation 🧺

The solution in the static linked list is ： How to use static simulation to allocate the storage space of dynamic linked list structure , Apply when necessary , Release when useless .

In the dynamic linked list , The application and release of nodes are borrowed separately malloc() and free() Two functions implement . In a static linked list , The operation is an array , There is no node application and release problem like dynamic linked list , So we need to implement these two functions ourselves , Can be inserted and deleted .

In order to identify which components in the array are not used , The solution is to link all unused and deleted components into a spare linked list with a cursor , When inserting , You can take the first node from the standby linked list as the new node to be inserted .

/*  If the spare space linked list is not empty , Then the allocated node subscript is returned , Otherwise return to  0 */
int Malloc_SLL(StaticLinkList space)
{
    
	/*  Of the first element of the current array  cur  Stored value , Is the first alternate free subscript to return  */
	int i = space[0].cur;
	/*  Because you have to take out a component to use , So we have to use its next component as a backup  */
	if (space[0].cur)
		space[0].cur = space[i].cur;
	return i;
}

This code , On the one hand, its function is to return a subscript value , This value is the value of the array header element cur The first free subscript saved . From the example shown above , It's just going back 7.

So since the subscript is 7 The weight of is ready to be used , You have to have a successor , So put the weight 7 Of cur Value is assigned to the header element , That is the 8 to space[0].cur, After that, you can continue to allocate new free components , The implementation is similar to malloc() Function function .

Now if we need to “ B ” and “ Ding ” Between , Insert a value of “ C ” The elements of , Store the structure in the previous order , You should “ Ding ”、“ E ”、“ Oneself ”、“ Geng ” These elements move back one bit . But there's no need for , Because we have new means .

The new element “ C ”, Want to jump the queue ？ Sure , You start quietly in the last row of the line 7 Hold a cursor position , I can take care of it for you in a minute . I then found “ B ”, Tell him , Yours cur The cursor is not 3 Of “ Ding ” 了 , This little money , It means , You change your next cursor to 7 That's all right. .“ B ” Sighed , I received the money cur The value has changed . Now go back to “ C ” Where? , Say you put your cur Change it to 3. That's it , Without the knowledge of most people , The order of the whole queue has changed . Pictured ：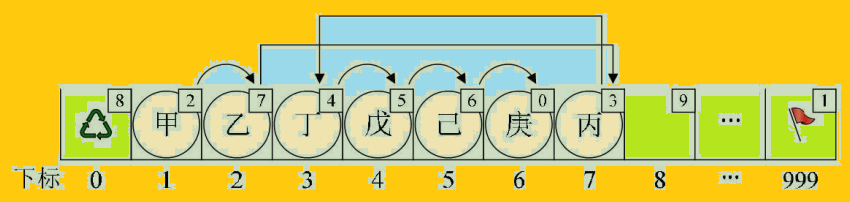

The implementation code of the above figure is as follows ：

/*  stay  L  pass the civil examinations  i  Insert a new data element before an element  e */
Status ListInsert(StaticLinkList L, int i, ElemType e)
{
    
	int j, k, l;
	/*  Be careful  k  The first is the subscript of the last element  */
	k = MAX_SIZE - 1;
	if (i < 1 || i > ListLength(L) + 1)
		return ERROR;
	/*  Get the subscript of the free component  */
	j = Malloc_SLL(L);
	if (j)
	{
    
		/*  Assign data to... Of this component data */         
		L[j].data = e;                           
		/*  Find No i The position before the first element  */         
		for (l = 1; l <= i - 1; l++)                 
			k = L[k].cur;         
		/*  The first i Before the first element cur Assigned to the new element cur */         
		L[j].cur = L[k].cur;                 
		/*  Assign the subscript of the new element to i Element before element cur */         
		L[k].cur = j;       
		return OK;
	}
	return ERROR;
} 

When we execute the insert statement , Our aim is to “ B ” and “ Ding ” Insert between “ C ”. When calling code , Input i The value is 3.
Give Way k = MAX_SIZE-1=999.
j = Malloc_SSL(L) = 7. Now the subscript is 0 Of cur Because 7 To be occupied, change the value of the standby linked list to 8.
for loop l from 1 To 2, Perform twice . Code k = L[k].cur ; bring k = 999, obtain k = L[999].cur = 1, To get k = L[1].cur = 2.
L[j].cur = L[k].cur ; because j = 7, and k = 2 obtain L[7].cur=L[2].cur = 3. This is what I said just now “ C ” It's cur Change it to 3 It means .
L[k].cur = j; It means L[2].cur = 7. Also is to let “ B ” Get some benefits , It's cur Change to point “ C ” The subscript 7.
That's it , We implemented the , Implementation does not move elements , The operation of inserting data .

(2) Static list delete operation

When deleting elements , Originally, it is a function that needs to release nodes free(). Now we must realize it by ourselves ：

/*  Delete on  L  pass the civil examinations  i  Elements  e */
Status ListDelete(StaticLinkList L, int i)
{
    
	int j, k;
	if (i < 1 || i > ListLength(L))
		return ERROR;
	k = MAX_SIZE - 1;
	for (j = 1; j <= i; j++)
		k = L[k].cur;
	j = L[k].cur;
	L[k].cur = L[i].cur;
	Free_SSL(L,j);  /*  See below  */
	return OK;
}

Mark the subscript as k The idle node of is recycled to the standby linked list code ：

/*  Mark the subscript as k The idle nodes are recycled to the spare list  */
void Free_SSL(StaticLinkList space, int k)
{
    
	/*  Put the first element  cur  Value is assigned to the component to be deleted  cur */
	space[k].cur = space[0].cur;
	/*  Assign the subscript of the component to be deleted to the... Of the first element  cur */
	space[0].cur = k;
}

A is leaving now , This position is empty ️, That is to say , In the future, if new people come , Top priority here , So the original first vacancy component , That is, the subscript is 8 Components of , It was downgraded , hold 8 to “ nail ” The subscript is 1 The component of cur, That is to say space[1].cur = space[0].cur = 8, and space[0].cur = k = 1 In fact, it is to make the deleted position the first priority vacancy , Put it in the... Of the first element cur in , Pictured :

(3) Advantages and disadvantages of static linked list

Upper figure ：

Conclusion