Mba-day28 concept of number - exercise questions

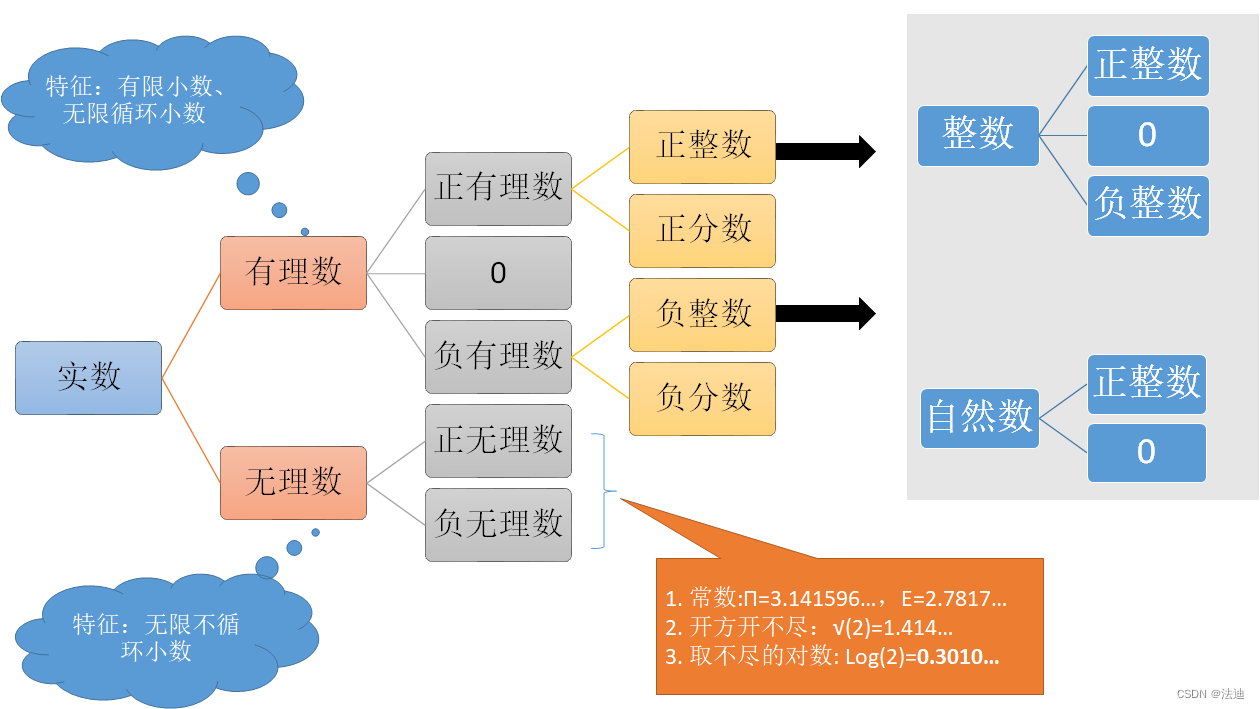
1. common ： The set of real Numbers 、 Rational number 、 Irrational number 、 Integers 、 The concept of natural numbers

• The set of real Numbers ： There are rational numbers and irrational numbers （ Infinite non recurring decimals ）
• Rational number ： Positive rational numbers ,0, Negative rational numbers
• Irrational number ： Positive irrational number , Negative irrational numbers （ constant 1. constant :Π=3.141596…,E=2.7817…2. There is no end to prescribing ：√(2)=1.414…3. Take infinite logarithms :Log(2)=0.3010…）
• Integers ： Positive integer ,0, Negtive integer
• Natural number ：0, Positive integer

2. Prime and sum

1. Prime number ： Only disassemble 1 And its own 2 A positive integer with a divisor , for example 7,11
2. Sum ： except 1 And a positive integer that has other divisors , for example 9,12
3. Prime and composite numbers have the following important properties

1. 20 The prime number within ：2,3,5,7,11,13,17,19
2. 2  Is a unique even prime number , Other prime numbers are odd numbers ( Except for the minimum prime number 2 It's even , Other prime numbers are odd numbers )
3.  The minimum prime number is 2
4.  Any composite number can be decomposed into prime numbers and multiplied . for example 8=2*2*2

4. Reciprocal number
5. The common divisor is 1 The two numbers of are called coprime numbers , for example 9 and 16

3. Odd and even numbers

1. Odd number ： Can not be 2 Divisible number
2. even numbers ： Can be 2 Divisible number , among 0 It's even
   Integers Z = Odd number and even numbers = 2n+1 and 2n

Be careful ： Two adjacent integers must be odd and even , Except for the minimum prime number 2 It's even , Other prime numbers are odd numbers

3. nature
   Both are even numbers , Different to odd

 Odd number  +  Odd number  =  even numbers 
 even numbers  +  even numbers  =  even numbers 
 Odd number  +  even numbers  =  Odd number 

4. Examination site

【】+【】= Odd number , Then it must be   An odd number an even number 
【】+【】+【】= Odd number , Then all are odd numbers , or   Two even numbers and one odd number 
【】+【】+【】= even numbers , Then all are even numbers , or   Two odd numbers and one even number 
 Prime number + Prime number = Prime number , Then there will be 2
 Prime number * Prime number = even numbers , Then there will be 2

4. to be divisible by 、 Multiple 、 Divisor

1. Division of numbers
2. greatest common divisor , for example (8, 12, 24) The approximate number is （2, 4）, The greatest common divisor is 4
3. Minimum common multiple , for example [8, 12, 24, 48], The multiple is (48,96…), The least common multiple 48
4. Finding the least common multiple

 for example [12, 15]
   3 |12, 15
      -------
       4  5
 Minimum common multiple ：3*4*5 = 60

a * b = [a, b]*(a, b) =  Minimum common multiple * greatest common divisor  = 60 * 3

5. Decomposing the prime factor
   seek [8,27,36,35] The least common multiple of

 The same factor is the most , Multiply by the unique factor 

8=2*2*2*2
27=3*3*3
36=2*2*3*3
35=5*7

[8,27,36,35]=2*2*2*2 * 3*3*3 * 5*7

6. A common characteristic of divisibility

• Can be 2 Divisible number ： Bits are even 0,2,4,6,8
• Can be 3 Divisible number ： The sum of the digits must be 3 to be divisible by
• Can be 9 Divisible number ： The sum of digits must be 9 to be divisible by
• Can be 5 Divisible number ： One digit 0 or 5
• Can be 6 Divisible number ： At the same time, satisfaction can be 2 and 3 The condition of division , Or can be 3 Even number of integral division
• Can be 10 Divisible number ： A bit must be 0
• Can be 11 Divisible number ： From right to left , The sum of odd digits minus the sum of even digits can be 11 to be divisible by （ Include 0）

 for example ：
3949 -> [(9+9) - (3+4) ]/ 11 = 1, That is, satisfaction can be 11 Divisible number 
286 -> [(2+6) - 8] / 11 = 0, That is, satisfaction can be 11 Divisible number 

Example 1:

set up m,n Less than 20 The prime number of , Meet the conditions |m-n| = 2 Set {m,n} And the combination (m,n) There are several groups ？

answer ：4 and 8 Group

 Explain ： Less than 20 The prime numbers of are as follows 
-> 2,3,5,7,11,13,17,19
 Meet the conditions |m-n| = 2 
 The collection has 4 The groups were respectively ：{3,5};{5,7};{11,13};{17,19}
 The combination has 8 The groups were respectively ：(3,5);(5,3);(5,7);(7,5);(11,13);(13,11);(17,19);(19,17)

 Gather knowledge points and expand ：
1. Set properties ： deterministic , Disorder , The opposite sex 
2. A subset of ： aggregate A The range is greater than or equal to the set B,B yes A Subset 
3. True subset ： aggregate A Range ratio B Big ,B yes A The proper subset of 

Example 2

If several prime numbers ( prime number ) The product of is 770, Ask for their sum ?

answer :25

 Explain :
-> Prime number :2,3,5,7.... except 2 It's even , The rest are odd numbers , There must be 2
-> Product of prime numbers :770  Decompose into prime numbers and multiply 
770 = 77 * 10 = 11 * 7 * 5 * 2
 So their harmony is =11+7+5+2 = 25

Example 3

Someone held several stones in his left and right hands , Multiply the left stone by 3 Add the number of stones in the right hand times 4 The sum is 29, Find the number of stones in your right hand ?

A: Odd number
B: even numbers
C: Prime number
D: Sum
E: None of the above is true

answer :C

 Explain :
 Let the number of stones in both hands be a,b
3a + 4b = 29
 Odd number + even numbers  =  Odd number 
 Eigenvalue method :
b = 1, a  Not an integer , dissatisfaction 
b = 2, a = 7
b = 3, a  Not an integer , dissatisfaction  
b = 4, a  Not an integer , dissatisfaction  
b = 5, a = 3
b = 6, a  Not an integer , dissatisfaction  
b = 7,  Greater than 29
 Therefore, the number of stones in the right hand is 2 or 5, Prime number 

Example 4

Utilization length is a and b The two kinds of pipes can be connected with a growth of 37 The pipe , Find the following conditional sufficiency .
1)a = 3, b = 5
2)a = 4, b = 6

answer : Conditions 1 to the full , Conditions 2 inadequate

 Explain :
 Respectively a,b Tube needs x,y Roots can be connected into  37  Meter pipe 
1)a = 3, b = 5
3x + 5y = 37
 Odd number + Odd number  =  Odd number 
 Start with the big number :
y = 1, 3, 5, 7, 11
y = 5, x = 4  Can meet the problem stem conditions 

2)2)a = 4, b = 6
4x + 6y = 37, Obviously , even numbers + even numbers   It is impossible to get an odd number 

 so : Conditions 1 to the full , Conditions 2 inadequate 

Example 5

The greatest common divisor of two positive integers a and B is 6, The minimum common multiple is 90, If the number of a is 18, Then B is m, seek m The sum of the digits of ?

answer :3

 Explain :
 Use the formula :a,b  Express 2 A positive integer , The product of two numbers :a x b =  greatest common divisor (a,b) x  Minimum common multiple [a,b]
18 x m = 6 * 90
m = 30

 so m The sum of the digits of =3+0 = 3

Example 6

A, B and C walk along 200 Meters of circular track running , A needs to finish a lap 1 branch 30 second , B needs to finish a lap 1 branch 20 second , C needs to finish a lap 1 branch 12 second
Three people start at the same time in the same direction , When the three first met at the starting point , Find the sum of the laps of a, B and C ?

answer :25 circle

 Explain :
 It takes a lap :90
 B runs a lap :80
 C ran a lap :72

 Three people start at the same time in the same direction , When the three first met at the starting point 
->  It shows that the time when the three met was t It's the same 
->  For the first time t It is the least common multiple of three people's time 
90 = 9 * 10
80 = 8 * 10
72 = 9 * 8
 Minimum common multiple =9 * 8 * 10 = 720
->  A, B, C and  = 720/90 + 720/80 + 720/72
= 8 + 9 + 10 = 25

Example 6

There are two double digits , The sum of the greatest common divisor and the least common multiple of these two two digits is 91, The least common multiple is the greatest common divisor 12 times , Then the larger of these two numbers is ()

The correct answer is 28, What I calculate is 42? Strange

 Explain :
 greatest common divisor (a,b) +  Minimum common multiple [a,b] = 91
 Minimum common multiple [a,b]= 12 x  greatest common divisor (a,b)
-> 13 x  greatest common divisor (a,b) = 91
->  greatest common divisor (a,b) = 7
->  Minimum common multiple [a,b] = 84
 The value needs to meet two digits , Therefore, the following relationship can be satisfied :
 greatest common divisor (a,b) *  Minimum common multiple [a,b] = a * b 
= 7 * 84 = 7 * 2 * 42 = 14 * 42, That is to say (14,42)
= 7 * 84 = 7 * 3 * 24 = 21 * 28, That is to say (21,28)

That is, the larger of the two numbers is 42

Example 7

It is known that the sum of the squares of two natural numbers is 900, The product of their greatest common divisor and least common multiple is 432. For this 2 The sum of natural numbers ()
answer :42

 Explain :
 Natural number :0  And positive integers 
 The sum of squares is 900:a^2 + b^2 = 900
->(a + b)^2 - 2ab = 900

 By the greatest common divisor (a,b) *  Minimum common multiple [a,b] = a * b = 432
->(a + b)^2 - 864 = 900
= (a + b)^2 = 1764 = 2 * 882 = 2 * 2 * 441 = 2 * 2 * 3 * 147 = 2 * 2* 3 * 3 * 7 * 7
= (a + b)^2= (2*3*7)^2
 namely a + b = 42

Example 8

The sum of the ages of a and B is a double digit , This two digit number is a prime number , The sum of the digits of this prime number is 13, A is just bigger than B 13 year , Then what is the product of the ages of Party A and Party B ?

answer :1080

 Explain :
 Let the ages of Party A and Party B be a, b
a + b = (11~97  The prime number in )
a = b + 13
->2b+13 = (11~97  The prime number in )
2b+13 = (15~97  The prime number in )
15,17,19,23,29,31,37,39,41,43,47,51,53,57,59,61,(67),71,73,79,83,87,91,93,97
 Only 67 The sum of all digits is 13
 so 2b + 13 = 67
b = 27
a = 40
 So the sum of their ages is  27 * 40 = 1080

Example 9

Three wires , The lengths are 120 centimeter ,180 centimeter , 300 centimeter , Now cut them into equal segments , There should be no remainder in each paragraph , Then at least it can be cut into （） paragraph .

answer ： At least it can be cut into （10） paragraph

 Explain ：
 Consider the greatest common divisor 
   10 |120 180 300
      ------------
      6 |12   18 30
        -----------
          2   3  5
 Now cut them into equal segments ,  Each paragraph 60 centimeter 
 The lengths are  120  centimeter ,180  centimeter , 300  centimeter , Can be cut separately ：120/60, 180/60, 300/60
 namely 2, 3, 5, That is, at least it can be cut into  10  paragraph 

Example 10

Three integers are known a, b, c The sum of is odd , also a - b = 3, that a,b,c The parity of is （）

A All three are odd numbers
B Two odd numbers and one even number
C One odd number, two even numbers
D All three are even numbers
E Undetermined

answer ：C

 Explain ：
a + b + c =  Odd number ( All odd numbers or 2 even numbers +1 Odd number )
a - b = 3 （a > b,  Odd and even ）
 namely ： One odd number, two even numbers 

Example 11

Positive integer m Divide 15 The remainder is 2
1） Positive integer m Divide 3 The remainder is 2
2） Positive integer m Divide 5 The remainder is 2

answer ： I.e. conditions 1 And conditions 2 Alone is not sufficient , Conditions 1 And conditions 2 Unite to fully

 Explain ：
1） Positive integer  m  Divide  3  The remainder is  2
 for example 8, Unable to launch : Positive integer  m  Divide  15  The remainder is 2

2） Positive integer  m  Divide  5  The remainder is  2
 for example 7, Unable to launch : Positive integer  m  Divide  15  The remainder is 2

1) and 2） union , shows m At least 15 Multiple +2, for example 17,  Satisfy 

 I.e. conditions 1 And conditions 2 Alone is not sufficient , Conditions 1 And conditions 2 Unite to fully 

Example 12

The sum of their ages must be odd .
1） The three people are of different ages
2） The ages of the three people are different prime numbers

answer ： Conditions 1 Alone is not sufficient , Conditions 2 Alone is not sufficient , The combination cannot be pushed out

 Explain ：
A + B + C =  Odd number 
 Satisfied situation ：
 even numbers + even numbers + Odd number  =  Odd number 
 Odd number + Odd number + Odd number  =  Odd number 

1） The three people are of different ages 
 Sum ： except 1 And a positive integer that has other divisors , for example  9,12
6+9+12= Odd number , Satisfy even number + even numbers + Odd number  =  Odd number 
9+27+6=42, even numbers , The sum of the three ages cannot be deduced alone must be odd 

2)  The ages of the three people are different prime numbers 
 Prime number ：2,3,5,7,11,13,17,19
2+3+5 = 10（ even numbers ）,  It is not satisfied that the three people are different prime numbers , The sum of the three ages cannot be deduced alone must be odd 

 answer ： Conditions 1 Alone is not sufficient , Conditions 2 Alone is not sufficient , The combination cannot be pushed out 

Example 13

A box of books , To give evenly to 6 Two children , redundant 1 Ben . To give evenly to 8 Two children , It's unnecessary 1 Ben . To give evenly to 9 Two children , There is also one more . This box has at least m Ben , be m The sum of the digits of is （）

answer ：10

 Explain ：
  6|m
   ---
    1
 Minimum :m/6 + 1, for example 7,49
    
  8|m
   ---
    1
 Minimum :m/8 + 1, for example 9,48

  9|m
   ---
    1
 Minimum :m/9 + 1, for example 10

 Description can be 6, 8, 9 Divide by whole to get the remainder 1, m = 6 * 8 * 9 + 1 = 433, The sum of the digits is =4+3+3= 10