当前位置:网站首页>ZOJ Problem Set – 2563 Long Dominoes 【如压力dp】
ZOJ Problem Set – 2563 Long Dominoes 【如压力dp】
2022-07-06 17:57:00 【全栈程序员站长】
大家好,又见面了,我是全栈君
称号:ZOJ Problem Set – 2563 Long Dominoes
题意:给出1*3的小矩形。求覆盖m*n的矩阵的最多的不同的方法数?
分析:有一道题目是1 * 2的。比較火。链接:这里
这个差点儿相同,就是当前行的状态对上一行有影响。对上上一行也有影响。所以
定义状态:dp【i】【now】【up】表示在第 i 行状态为now 。上一行状态为 up 时的方案数。
然后转移方程:dp【i】【now】【up】 = sum ( dp【i-1】【up】【uup】 ) 前提是合法
合法性的推断是比較难考虑的一点。由于是1 * 3的。仅仅能横着放和竖着放。
假设横着放。那么上面up 和 uup 的 3 格也必须是满的才行
假设竖着放,那么up 和 uup的当前格必须是空的,注意推断后变化up
假设用简单的枚举dp的话,四层循环会超时。所以我们要用up 和 upp 来深搜构造当前行,这样才干过。
AC代码:
#include <cstdio>
#include <cstring>
#include <string>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
#define INT long long int
const long long N = 9 ;
const int inf = 0x3f3f3f3f;
INT dp[31][1<<N][1<<N];
int m,n;
bool Judge(int s,int up,int upp)
{
for(int i=s;i<s+3;i++)
if(!(up&(1<<i)) || !(upp&(1<<i)))
return false;
return true;
}
void dfs(int st,int cnt,int now,int up,int upp,INT num)
{
if(cnt==m)
{
dp[st][now][up]+=num;
return ;
}
if(cnt+3<=m && Judge(cnt,up,upp)) //heng
dfs(st,cnt+3,now|(1<<cnt)|(1<<(cnt+1))|(1<<(cnt+2)),up,upp,num);
if(!(up&(1<<cnt))&&!(upp&(1<<cnt))) // 竖放
dfs(st ,cnt+1 ,now|(1<<cnt) ,up|(1<<cnt) ,upp , num) ;
if(upp&(1<<cnt)) //留空
dfs(st ,cnt+1 ,now ,up ,upp ,num) ;
}
int main()
{
while(~scanf("%d%d",&m,&n)&& m+n)
{
memset(dp,0,sizeof(dp));
dfs(1,0,0,(1<<m)-1,(1<<m)-1,1);
for(int i=2; i<=n; i++)
{
for(int up=0; up<(1<<m); up++) //上行
{
for(int st=0; st<(1<<m); st++) //上上行
{
if(dp[i-1][up][st]) //注意一定推断
dfs(i,0,0,up,st,dp[i-1][up][st]);
}
}
}
printf("%lld\n",dp[n][(1<<m)-1][(1<<m)-1]);
}
return 0;
}枚举超时代码:
#include <cstdio>
#include <cstring>
#include <string>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
#define INT long long int
const long long N = 9 ;
const int inf = 0x3f3f3f3f;
INT dp[31][1<<N][1<<N];
int m,n;
bool isit(int st)
{
int tmp=0;
for(int i=0;i<m;i++)
{
if(st&(1<<i))
tmp++;
else
{
if(tmp%3)
return false;
}
}
if(tmp%3)
return false;
return true;
}
INT solve(int now,int up,int uup)
{
for(int i=0;i<m;i++)
{
if(!(uup&(1<<i))) //推断上上一行为0
{
if(up&(1<<i))
return -1 ;
else
{
if(!(now&(1<<i)))
return -1 ;
else
up |= (1<<i) ;
}
}
else
{
if(up&(1<<i) && now&(1<<i)) // 1 1 1
{
if(i==m-2 || i==m-1)
return -1 ;
else if(!(now&(1<<(i+1))) || !(now&(1<<(i+2))) || !(up&(1<<(i+1))) || !(up&(1<<(i+2))) || !(uup&(1<<(i+2))) || !(uup&(1<<(i+1))))
return -1 ;
i+=2;
}
}
}
return up ;
}
int main()
{
while(~scanf("%d%d",&m,&n)&& m+n)
{
for(int st=0;st<(1<<m);st++)
{
if(!isit(st))
continue;
for(int up=0;up<(1<<m);up++)
{
if(isit(up)){
dp[2][st][up]=1;
}
}
}
for(int i=3;i<=n;i++)
{
for(int no = 0;no < (1<<m); no++)
{
for(int kp=0;kp<(1<<m);kp++) //上行
dp[i][no][kp]=0;
for(int up=0;up<(1<<m);up++) //上行
{
int temp ;
for(int st=0;st<(1<<m);st++) //上上行
if((temp = solve(no,up,st)) != -1)
dp[i][no][temp]+=dp[i-1][up][st];
//printf("%d\n",dp[i][up][up]);
}
}
}
printf("%lld\n",dp[n][(1<<m)-1][(1<<m)-1]);
}
return 0;
}版权声明:本文博主原创文章,博客,未经同意不得转载。
发布者:全栈程序员栈长,转载请注明出处:https://javaforall.cn/116912.html原文链接:https://javaforall.cn
边栏推荐
- ARM裸板调试之JTAG调试体验
- golang 基础 —— 数据类型
- How to evaluate load balancing performance parameters?
- 从零开始匹配vim(0)——vimscript 简介
- HMM 笔记
- Typical problems of subnet division and super network construction
- Installation and testing of pyflink
- Go zero micro service practical series (IX. ultimate optimization of seckill performance)
- 今日问题-2022/7/4 lambda体中修改String引用类型变量
- C语言实例_2
猜你喜欢
一起看看matlab工具箱内部是如何实现BP神经网络的
![[signal and system]](/img/aa/a65d6da1d1d9410254ca7b775e24a6.png)
[signal and system]
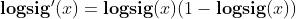
tansig和logsig的差异,为什么BP喜欢用tansig
【C语言进阶篇】指针的8道笔试题

身体质量指数程序,入门写死的小程序项目

Byte P7 professional level explanation: common tools and test methods for interface testing, Freeman
AI automatically generates annotation documents from code
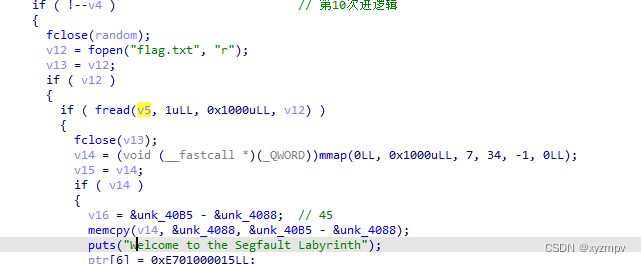
2022 Google CTF segfault Labyrinth WP

Clickhouse fields are grouped and aggregated, and SQL is queried according to the granularity of any time period
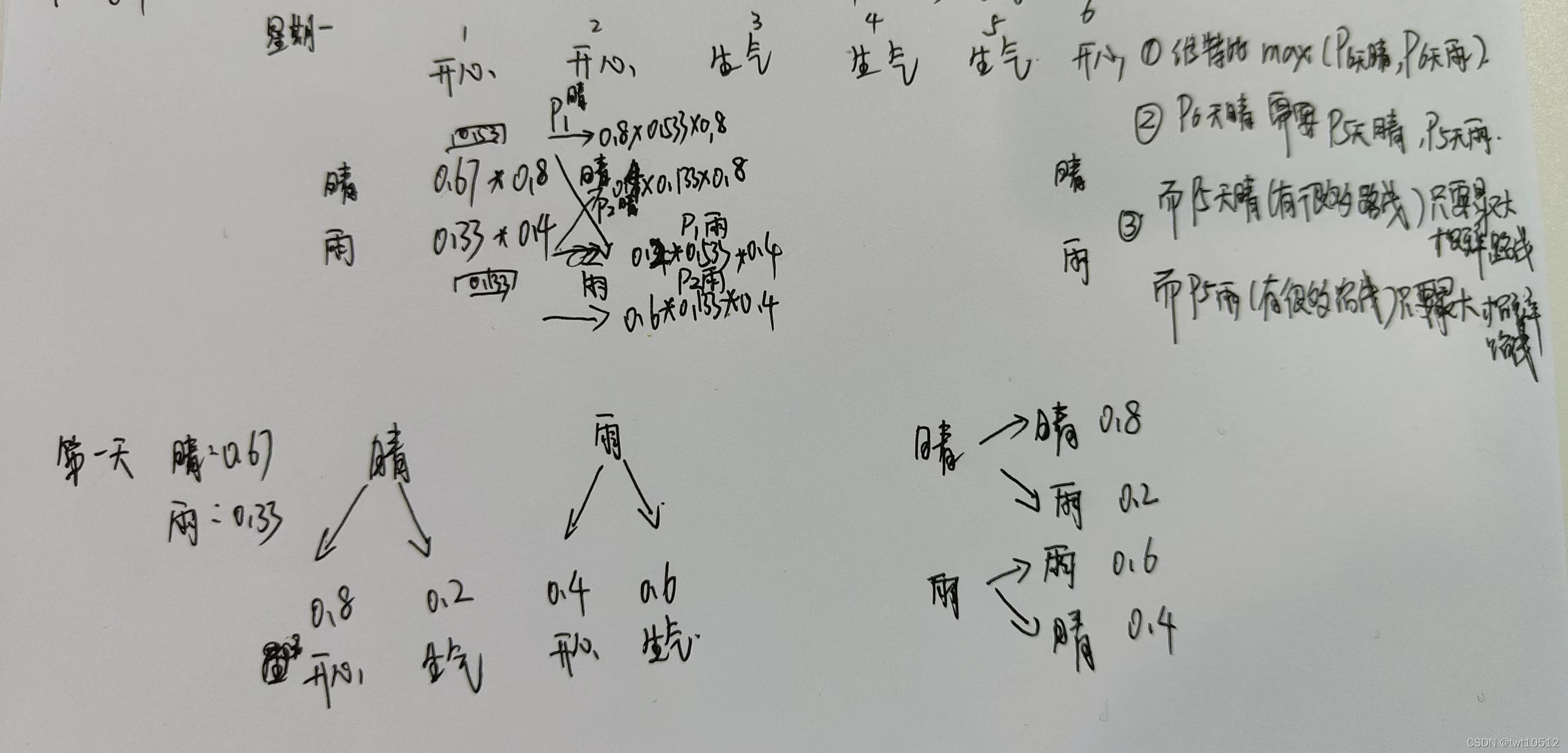
HMM notes
随机推荐
table表格设置圆角
Taro中添加小程序 “lazyCodeLoading“: “requiredComponents“,
C语言实例_3
系统休眠文件可以删除吗 系统休眠文件怎么删除
C language instance_ five
从底层结构开始学习FPGA----FIFO IP的定制与测试
[chip scheme design] pulse oximeter
Taro applet enables wxml code compression
C language instance_ four
负载均衡性能参数如何测评?
字节P7专业级讲解:接口测试常用工具及测试方法,福利文
1123. The nearest common ancestor of the deepest leaf node
Make Jar, Not War
【C语言进阶篇】指针的8道笔试题
分享一个通用的so动态库的编译方法
【芯片方案设计】脉搏血氧仪
搭建【Redis in CentOS7.x】
Can the system hibernation file be deleted? How to delete the system hibernation file
How to evaluate load balancing performance parameters?
Oracle: Practice of CDB restricting PDB resources