当前位置:网站首页>数电快速入门(一)(BCD码和三种基本逻辑运算的介绍)
数电快速入门(一)(BCD码和三种基本逻辑运算的介绍)
2022-08-04 21:04:00 【小林学编程】
1.1 二-十进制码(BCD码)
定义:为了方便数字系统处理十进制数,经常采用编码的方法,即以若干位二进制码来表示1位十进制数,这种代码称为二-十进制码,或BCD码,其中常用的BCD码有8421BCD码、5421BCD码、2421BCD码、余3码,其中最常用的BCD码为8421BCD码。
1.2 8421BCD码
8421BCD码用于表示数字0-9(其余10-16数字为无用数组)分别为:
0000,0001,0010,0011,0100,0101,0110,0111,1000,1001
(可以简单记成由二进制来表示的数字,因为有这样的性质,所以8421BCD码也被称为有权码)
简单举例:如何判断是否为有权码?
0010=0*2^0+1*2^1+0*2^2+0*2^3=1,因为四位二进制码中的权重比可以直接用权值代替从而得出正确的十进制数,且每一位的权值分别为1,2,4,8,所以此为有权码8421码。
1.3 格雷码
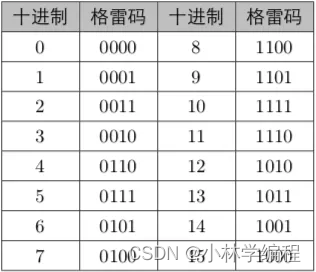 左图为格雷码的表示0-9数字方式,我们很容易可以发现这是一种无权码。 这种码的特点是:相邻两个数字之间的代码之间差距仅有1位不同,其余各位均相同,所以又被称为循环码。 这种码的好处是:在模拟量和数字量之间转换时,只需改变一位数,减小出错的可能性。 这种码的缺点:因为格雷码无固定的权,所以在数字系统中不能直接计算,需要转化成普通的二进制码。
左图为格雷码的表示0-9数字方式,我们很容易可以发现这是一种无权码。 这种码的特点是:相邻两个数字之间的代码之间差距仅有1位不同,其余各位均相同,所以又被称为循环码。 这种码的好处是:在模拟量和数字量之间转换时,只需改变一位数,减小出错的可能性。 这种码的缺点:因为格雷码无固定的权,所以在数字系统中不能直接计算,需要转化成普通的二进制码。
1.4.1 基本逻辑运算
0:真值表的定义
定义:真值表使用表格的形式全面、直观地描述所有的输入变量(前提条件),取值的各种可能组合和对应的输出变量
1:‘与’逻辑运算
一般定义:只有一件事的条件都具备时,这件事才成立。
‘与’逻辑的代数表达式(A、B为条件):

注:这里的相乘和代数相乘不同,在本系列(二)中基本定律中会具体讲解。
‘与’逻辑的真值表:
| A | B | F=AB |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
‘与’逻辑的逻辑功能概括:
有0出0,全1出1(我们可以从真值表中看出,当A或B有一个为0时,F=0;当A和B全为1时,F=1.)
2:‘或’逻辑运算
一般定义:只有一件事的条件有一件具时,这件事就能成立。
‘或’逻辑的代数表达式(A、B为条件):
F=A+B
注:这里的相加和代数相加不同,在本系列(二)中基本定律中会具体讲解。
‘或’逻辑的真值表:
| A | B | F=A+B |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
‘或’逻辑的逻辑功能概括:
有1出1,全0出0(我们可以从真值表中看出,当A或B有一个为1时,F=1;当A和B全为0时,F=0)
3:'非'逻辑运算
一般定义:只有一件事的条件不具备时,这件事才成立。
‘非’逻辑的代数表达式(A为条件):

‘非’逻辑的真值表:
| A |  |
| 1 | 0 |
| 0 | 1 |
以上三种逻辑关系为数字电路中最基本逻辑关系。
边栏推荐
猜你喜欢
LayaBox---TypeScript---Problems encountered at first contact

Five Minutes Introductory Text Processing Three Musketeers grep awk sed
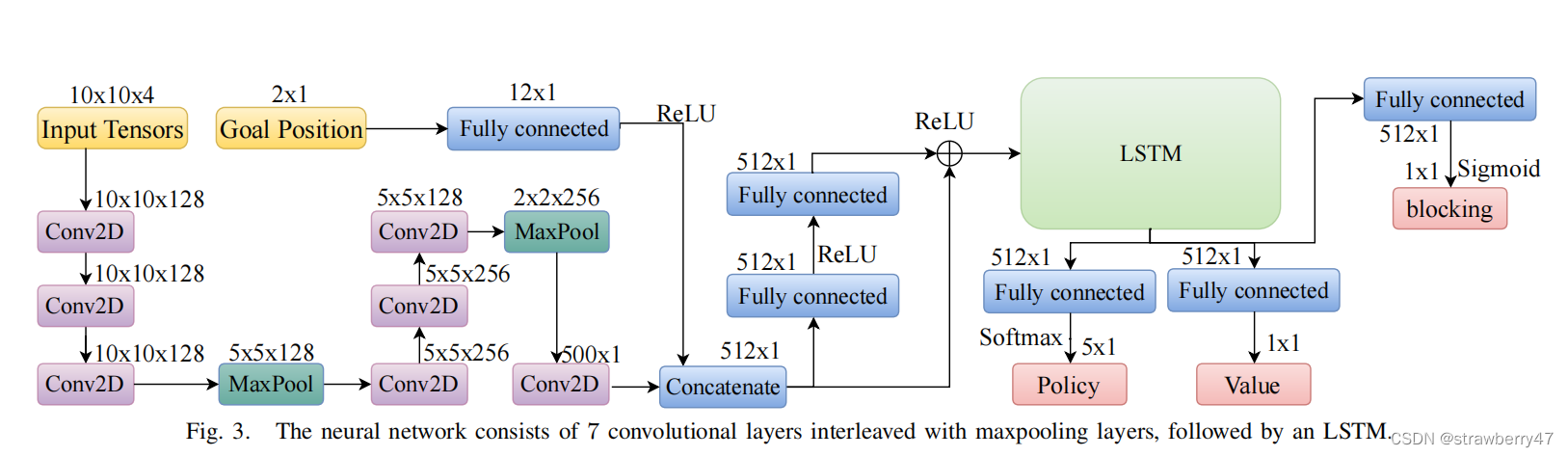
PRIMAL: Pathfinding via Reinforcement and Imitation Multi-Agent Learning 代码解析

How to make good use of builder mode
二叉搜索树解决硬木问题

for 循环中的 ++i 与 i++
![[2022 Hangzhou Electric Power Multi-School 5 1012 Questions Buy Figurines] Application of STL](/img/fe/1dd9418800366ee25067e154936e3b.png)
[2022 Hangzhou Electric Power Multi-School 5 1012 Questions Buy Figurines] Application of STL
DICOM医学影像协议

【学术相关】清华教授发文劝退读博:我见过太多博士生精神崩溃、心态失衡、身体垮掉、一事无成!...
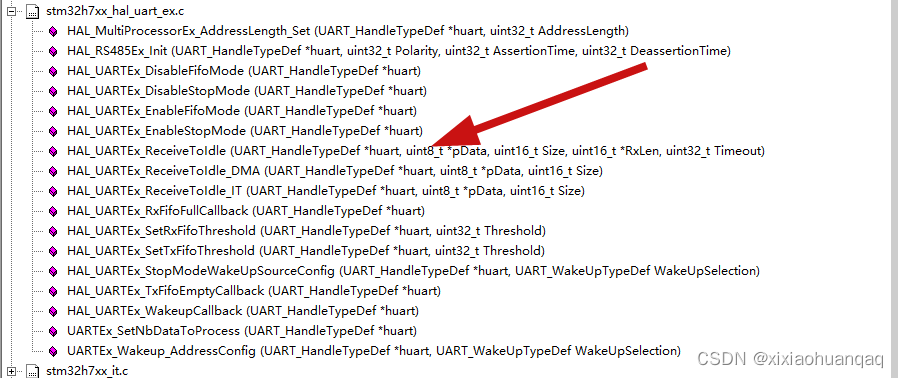
【手把手教你使用STM32HAL库的串口空闲中断】
随机推荐
结构体小结
SPSS-System Clustering Hand Calculation Practice
Win10 uwp use ScaleTransform magnify an element
密码学系列之:PEM和PKCS7,PKCS8,PKCS12
漫画 | 老板裁掉我两周后,又把我请回去,工资翻番!
IPV6地址
DSPE-PEG-Aldehyde, DSPE-PEG-CHO, Phospholipid-Polyethylene Glycol-Aldehyde A hydrophobic 18-carbon phospholipid
PRIMAL: Pathfinding via Reinforcement and Imitation Multi-Agent Learning Code Analysis
1、File对象学习
无代码平台字段设置:基础设置入门教程
idea2021版本添加上一步和下一步操作到工具栏
Data warehouse (1) What is data warehouse and what are the characteristics of data warehouse
How to understand the crawler's Scrapy framework in the simplest and most popular way?
[Data Mining] Written Exam Questions for Sohu Data Mining Engineers
[AGC] Build Service 1 - Cloud Function Example
【随记】新一天搬砖 --20220727
dotnet 通过 WMI 获取系统安装软件
模拟对抗之红队免杀开发实践
Big capital has begun to flee the crypto space?
PCBA方案设计——厨房语音秤芯片方案