当前位置:网站首页>[the Nine Yang Manual] 2021 Fudan University Applied Statistics real problem + analysis
[the Nine Yang Manual] 2021 Fudan University Applied Statistics real problem + analysis
2022-07-06 13:31:00 【Elder martial brother statistics】
The real part
One 、(15 branch ) There are countless lines with a distance of 2 Equidistant parallel lines of , First throw one side as 1 An equilateral triangle , Find the probability that the triangle intersects the parallel line .
Two 、(15 branch ) Party A and Party B toss coins , If the front is up, a wins 1 element , Reverse up B wins 1 element . Together with 20 round , In the end, neither of them will lose or win . It is known that a has no money at first , Ask the probability that a doesn't owe money in the whole process .
3、 ... and 、(15 branch ) X 0 , ⋯ , X n , ⋯ X_0,\cdots,X_n,\cdots X0,⋯,Xn,⋯ yes i.i.d. To obey U ( 0 , 1 ) U(0,1) U(0,1) Random variable of , remember
N = inf { n ≥ 1 : X n > X 0 } , N=\inf \{ n\ge1:X_n>X_0 \}, N=inf{ n≥1:Xn>X0}, seek N N N The distribution law of .
Four 、(15 branch ) X 1 , ⋯ , X n X_1,\cdots,X_n X1,⋯,Xn yes i.i.d. Random variable of , P ( X = 1 ) = 0.4 , P ( X = − 0.5 ) = 0.6 \mathrm{P}(X=1)=0.4,\mathrm{P}(X=-0.5)=0.6 P(X=1)=0.4,P(X=−0.5)=0.6. Make S n = ( 1 + X 1 ) ( 1 + X 2 ) ⋯ ( 1 + X n ) S_n=(1+X_1)(1+X_2)\cdots(1+X_n) Sn=(1+X1)(1+X2)⋯(1+Xn), ask E ( S n ) \mathrm{E}(S_n) E(Sn) And S n S_n Sn Convergence or not ? If convergence , Find its limit .
5、 ... and 、(15 branch ) Toss a coin , If the same surface appears three times in a row, it will stop , Record the number of throws as N N N, seek E N \mathrm{E}N EN.
6、 ... and 、(15 branch ) X 1 , X 2 X_1,X_2 X1,X2 Independence and obedience N ( 0 , 1 ) N(0,1) N(0,1), seek X 1 X 2 \frac{X_1}{X_2} X2X1 And X 1 2 X 2 2 \frac{X_{1}^2}{X_{2}^2} X22X12 The distribution of .
7、 ... and 、(10 branch ) Short answer :
(1)(5 branch ) Describe the definition of sufficient statistics .
(2)(5 branch ) Narration C-R inequality .
8、 ... and 、(10 branch ) Some come from the general f ( x ) = 2 x , 0 < x < 1 f(x)=2x,0<x<1 f(x)=2x,0<x<1 Of 10 Random sample X 1 , ⋯ , X 10 X_1,\cdots,X_{10} X1,⋯,X10, ask X ( 3 ) X ( 6 ) \frac{X_{(3)}}{X_{(6)}} X(6)X(3) And X ( 6 ) X_{(6)} X(6) Is it independent , Please give reasons .
Nine 、(10 branch ) Some come from the general N ( μ , 1 ) N(\mu,1) N(μ,1) Of n n n Random sample X 1 , ⋯ , X n X_1,\cdots,X_n X1,⋯,Xn, prove : X ˉ \bar{X} Xˉ It's full statistics .
Ten 、(10 branch ) Some come from the general U ( θ , 2 θ ) U(\theta,2\theta) U(θ,2θ) Of n n n Random sample X 1 , ⋯ , X n X_1,\cdots,X_n X1,⋯,Xn, seek θ \theta θ Maximum likelihood estimation of , And judge its unbiasedness and consistency .
11、 ... and 、(10 branch ) Some come from the general N ( μ , σ 2 ) N(\mu,\sigma^2) N(μ,σ2) Of n n n Random sample X 1 , ⋯ , X n X_1,\cdots,X_n X1,⋯,Xn, among μ \mu μ It is known that , Make
σ ^ = 1 n π 2 ∑ i = 1 n ∣ X i − μ ∣ , \hat{\sigma}=\frac{1}{n}\sqrt{\frac{\pi}{2}}\sum_{i=1}^n{\left| X_i-\mu \right|}, σ^=n12πi=1∑n∣Xi−μ∣, verification σ ^ \hat{\sigma} σ^ yes σ \sigma σ Unbiased estimation of , But it is not an effective estimate .
Twelve 、(10 branch ) Some come from the general P ( θ ) \mathcal P(\theta) P(θ) Of n n n Random sample , Consider the hypothesis test problem :
H 0 : θ = 2 v s H 1 : θ = 3 , \mathrm{H}_0:\theta=2 \quad \mathrm{vs} \quad \mathrm{H}_1:\theta=3, H0:θ=2vsH1:θ=3, There are denial domains W = { x ˉ ≥ 2.8 } W=\{ \bar{x} \ge 2.8\} W={ xˉ≥2.8}, ask
(1)(5 branch ) n = 5 n=5 n=5 when , What is the probability of making two kinds of mistakes ?
(2)(5 branch ) n n n Towards infinity , What happens to the probability of making two kinds of mistakes ? Please explain .
The analysis part
One 、(15 branch ) There are countless lines with a distance of 2 Equidistant parallel lines of , First throw one side as 1 An equilateral triangle , Find the probability that the triangle intersects the parallel line .
Solution:
remember △ A B C \triangle A B C △ABC The three sides of the are a , b , c a, b, c a,b,c. Then there are the following situations when a triangle intersects a parallel line :(1) One vertex of the triangle is on the parallel line ; (2) One side of the triangle coincides with the straight line ; (3) Two lines of triangle Edges intersect parallel lines .
According to the geometric probability P ( 1 ) = P ( 2 ) = 0 P(1)=P(2)=0 P(1)=P(2)=0, So just consider the situation (3). and P ( 3 ) = P a b + P a c + P b c P(3)=P_{a b}+P_{a c}+P_{b c} P(3)=Pab+Pac+Pbc, among P a b P_{a b} Pab edge a 、 b a 、 b a、b Intersect with parallel lines . So , remember P a P_{a} Pa edge a a a Intersect with parallel lines , be P a = P a c + P a b P_{a}=P_{a c}+P_{a b} Pa=Pac+Pab. so P ( 3 ) = 1 2 ( P a + P b + P c ) , P(3)=\frac{1}{2}\left(P_{a}+P_{b}+P_{c}\right), P(3)=21(Pa+Pb+Pc), Now we only need to find P a 、 P b 、 P c P_{a} 、 P_{b} 、 P_{c} Pa、Pb、Pc. This is a Buffon Injection model , The probability is P a = 2 a d π P_{a}=\frac{2 a}{d \pi} Pa=dπ2a, among a a a Is the edge a a a The length of , d d d It's parallel Spacing between lines , Substituting data can be calculated P a = 2 2 π = 1 π P_{a}=\frac{2}{2 \pi}=\frac{1}{\pi} Pa=2π2=π1. Empathy P b = P c = 1 π P_{b}=P_{c}=\frac{1}{\pi} Pb=Pc=π1. so
P { Triangle pressed to a straight line } = P ( 3 ) = 1 2 ( P a + P b + P c ) = 3 2 π . P\{\text { Triangle pressed to a straight line }\}=P(3)=\frac{1}{2}\left(P_{a}+P_{b}+P_{c}\right)=\frac{3}{2 \pi}. P{ Triangle pressed to a straight line }=P(3)=21(Pa+Pb+Pc)=2π3.
Two 、(15 branch ) Party A and Party B toss coins , If the front is up, a wins 1 element , Reverse up B wins 1 element . Together with 20 round , In the end, neither of them will lose or win . It is known that a has no money at first , Ask the probability that a doesn't owe money in the whole process .
Solution:
Use the broken line method , The problem is : From the point of ( 0 , 0 ) (0,0) (0,0) Random walk to point ( 20 , 0 ) (20,0) (20,0), Do not touch the straight line during y = − 1 y=-1 y=−1. First , From the point of ( 0 , 0 ) (0,0) (0,0) Random walk to point ( 20 , 0 ) (20,0) (20,0) A total of C 20 10 C_{20}^{10} C2010 Kind of (20 Next time , A win 10 Time ). From the point of ( 0 , 0 ) (0,0) (0,0) Random walk to and ( 20 , 0 ) (20,0) (20,0) About y = − 1 y=-1 y=−1 Symmetrical points ( 20 , − 2 ) (20,-2) (20,−2) There are kinds in total C 20 9 C_{20}^{9} C209 Kind of . so Suppose the probability of the event is :
P ( A ) = 1 − C 20 9 C 20 10 = 1 11 . \mathrm{P}(A)=1-\frac{C_{20}^{9}}{C_{20}^{10}}=\frac{1}{11}. P(A)=1−C2010C209=111.
3、 ... and 、(15 branch ) X 0 , ⋯ , X n , ⋯ X_0,\cdots,X_n,\cdots X0,⋯,Xn,⋯ yes i.i.d. To obey U ( 0 , 1 ) U(0,1) U(0,1) Random variable of , remember
N = inf { n ≥ 1 : X n > X 0 } , N=\inf \{ n\ge1:X_n>X_0 \}, N=inf{ n≥1:Xn>X0}, seek N N N The distribution law of .
Solution:
First calculate the given X 0 = x X_{0}=x X0=x Conditional distribution of time , It is similar to geometric distribution :
P ( N = k ∣ X 0 = x ) = P k − 1 ( X 1 ≤ x ) P ( X k > x ) = x k − 1 ( 1 − x ) \begin{aligned} \mathrm{P}\left(N=k \mid X_{0}=x\right) &=\mathrm{P}^{k-1}\left(X_{1} \leq x\right) \mathrm{P}\left(X_{k}>x\right) \\ &=x^{k-1}(1-x) \end{aligned} P(N=k∣X0=x)=Pk−1(X1≤x)P(Xk>x)=xk−1(1−x) By the formula of total probability in continuous occasions , Yes P ( N = k ) = ∫ 0 1 x k − 1 ( 1 − x ) d x = 1 k ( k + 1 ) \mathrm{P}(N=k)=\int_{0}^{1} x^{k-1}(1-x) d x=\frac{1}{k(k+1)} P(N=k)=∫01xk−1(1−x)dx=k(k+1)1.
Four 、(15 branch ) X 1 , ⋯ , X n X_1,\cdots,X_n X1,⋯,Xn yes i.i.d. Random variable of , P ( X = 1 ) = 0.4 , P ( X = − 0.5 ) = 0.6 \mathrm{P}(X=1)=0.4,\mathrm{P}(X=-0.5)=0.6 P(X=1)=0.4,P(X=−0.5)=0.6. Make S n = ( 1 + X 1 ) ( 1 + X 2 ) ⋯ ( 1 + X n ) S_n=(1+X_1)(1+X_2)\cdots(1+X_n) Sn=(1+X1)(1+X2)⋯(1+Xn), ask E ( S n ) \mathrm{E}(S_n) E(Sn) And S n S_n Sn Convergence or not ? If convergence , Find its limit .
Solution:
E ( S n ) = ∏ i = 1 n E ( 1 + X i ) = ( 1.1 ) n → + ∞ \mathrm{E}\left(S_{n}\right)=\prod_{i=1}^{n} \mathrm{E}\left(1+X_{i}\right)=(1.1)^{n} \rightarrow+\infty E(Sn)=∏i=1nE(1+Xi)=(1.1)n→+∞, Expectation does not converge ; By strong law of numbers
1 n ln S n = 1 n ∑ i = 1 n ln ( 1 + X i ) * a.s. Eln ( 1 + X 1 ) = − 1 5 ln 2 < 0 \frac{1}{n} \ln S_{n}=\frac{1}{n} \sum_{i=1}^{n} \ln \left(1+X_{i}\right) \stackrel{\text { a.s. }}{\longrightarrow} \operatorname{Eln}\left(1+X_{1}\right)=-\frac{1}{5} \ln 2<0 n1lnSn=n1∑i=1nln(1+Xi)* a.s. Eln(1+X1)=−51ln2<0,
so S n * a.s. lim n → ∞ exp { − n 5 ln 2 } = 0. S_{n} \stackrel{\text { a.s. }}{\longrightarrow} \lim _{n \rightarrow \infty} \exp \left\{-\frac{n}{5} \ln 2\right\}=0 . Sn* a.s. limn→∞exp{ −5nln2}=0.
5、 ... and 、(15 branch ) Toss a coin , If the same surface appears three times in a row, it will stop , Record the number of throws as N N N, seek E N \mathrm{E}N EN.
Solution:
set up A − 2 , A − 1 , A 0 , A 1 , A 2 A_{-2}, A_{-1}, A_{0}, A_{1}, A_{2} A−2,A−1,A0,A1,A2 They are states “ Just cast continuously 2 The second reverse ”、“ Just cast continuously 1 The second reverse ”、 The initial state ”、“ Just cast continuously 1 Suboptimal ”、“ Just cast continuously 2 Suboptimal ”. set up X X X Indicates starting from the current state , The number of times to stop on the same side for three consecutive times , Then there are :
E [ X ∣ A − 2 ] = 1 2 + 1 2 ( E [ X ∣ A 1 ] + 1 ) E [ X ∣ A − 1 ] = 1 2 ( E [ X ∣ A − 2 ] + 1 ) + 1 2 ( E [ X ∣ A 1 ] + 1 ) E [ X ∣ A 0 ] = 1 2 ( E [ X ∣ A − 1 ] + 1 ) + 1 2 ( E [ X ∣ A 1 ] + 1 ) E [ X ∣ A 1 ] = 1 2 ( E [ X ∣ A − 1 ] + 1 ) + 1 2 ( E [ X ∣ A 2 ] + 1 ) E [ X ∣ A 2 ] = 1 2 + 1 2 ( E [ X ∣ A − 1 ] + 1 ) \begin{aligned} \mathrm{E}\left[X \mid A_{-2}\right] &=\frac{1}{2}+\frac{1}{2}\left(\mathrm{E}\left[X \mid A_{1}\right]+1\right) \\ \mathrm{E}\left[X \mid A_{-1}\right] &=\frac{1}{2}\left(\mathrm{E}\left[X \mid A_{-2}\right]+1\right)+\frac{1}{2}\left(\mathrm{E}\left[X \mid A_{1}\right]+1\right) \\ E\left[X \mid A_{0}\right] &=\frac{1}{2}\left(\mathrm{E}\left[X \mid A_{-1}\right]+1\right)+\frac{1}{2}\left(\mathrm{E}\left[X \mid A_{1}\right]+1\right) \\ \mathrm{E}\left[X \mid A_{1}\right] &=\frac{1}{2}\left(\mathrm{E}\left[X \mid A_{-1}\right]+1\right)+\frac{1}{2}\left(\mathrm{E}\left[X \mid A_{2}\right]+1\right) \\ \mathrm{E}\left[X \mid A_{2}\right] &=\frac{1}{2}+\frac{1}{2}\left(\mathrm{E}\left[X \mid A_{-1}\right]+1\right) \end{aligned} E[X∣A−2]E[X∣A−1]E[X∣A0]E[X∣A1]E[X∣A2]=21+21(E[X∣A1]+1)=21(E[X∣A−2]+1)+21(E[X∣A1]+1)=21(E[X∣A−1]+1)+21(E[X∣A1]+1)=21(E[X∣A−1]+1)+21(E[X∣A2]+1)=21+21(E[X∣A−1]+1) Obviously, the problem has symmetry , set up
x = E [ X ∣ A − 2 ] = E [ X ∣ A 2 ] , y = E [ X ∣ A − 1 ] = E [ X ∣ A 1 ] , z = E [ X ∣ A 0 ] , x=E\left[X \mid A_{-2}\right]=E\left[X \mid A_{2}\right], y=E\left[X \mid A_{-1}\right]=E\left[X \mid A_{1}\right], z=E\left[X \mid A_{0}\right], x=E[X∣A−2]=E[X∣A2],y=E[X∣A−1]=E[X∣A1],z=E[X∣A0],
There are
{ x = 1 2 + 1 2 ( y + 1 ) , y = 1 2 ( x + 1 ) + 1 2 ( y + 1 ) , z = 1 2 ( y + 1 ) + 1 2 ( y + 1 ) , * { x − 1 2 y = 1 , x − y = − 2 , z = y + 1 , * { x = 4 , y = 6 , z = 7. \begin{cases} x=\frac{1}{2}+\frac{1}{2}\left( y+1 \right) ,\\ y=\frac{1}{2}\left( x+1 \right) +\frac{1}{2}\left( y+1 \right) ,\\ z=\frac{1}{2}\left( y+1 \right) +\frac{1}{2}\left( y+1 \right) ,\\ \end{cases}\Longrightarrow \begin{cases} x-\frac{1}{2}y=1,\\ x-y=-2,\\ z=y+1,\\ \end{cases}\Longrightarrow \begin{cases} x=4,\\ y=6,\\ z=7.\\ \end{cases} ⎩⎪⎨⎪⎧x=21+21(y+1),y=21(x+1)+21(y+1),z=21(y+1)+21(y+1),*⎩⎪⎨⎪⎧x−21y=1,x−y=−2,z=y+1,*⎩⎪⎨⎪⎧x=4,y=6,z=7. so E N = E [ X ∣ A 0 ] = 7 \mathrm{E} N=\mathrm{E}\left[X \mid A_{0}\right]=7 EN=E[X∣A0]=7.
6、 ... and 、(15 branch ) X 1 , X 2 X_1,X_2 X1,X2 Independence and obedience N ( 0 , 1 ) N(0,1) N(0,1), seek X 1 X 2 \frac{X_1}{X_2} X2X1 And X 1 2 X 2 2 \frac{X_{1}^2}{X_{2}^2} X22X12 The distribution of .
Solution:
Y = X 1 X 2 ∼ Cau ( 0 , 1 ) Y=\frac{X_{1}}{X_{2}} \sim \operatorname{Cau}(0,1) Y=X2X1∼Cau(0,1), Make Z = Y 2 Z=Y^{2} Z=Y2,
P ( Z ≤ z ) = P ( − z ≤ Y ≤ z ) = 2 ∫ 0 z 1 π ( 1 + x 2 ) d x = 2 π arctan z \begin{aligned} \mathrm{P}(Z \leq z) &=\mathrm{P}(-\sqrt{z} \leq Y \leq \sqrt{z}) \\ &=2 \int_{0}^{\sqrt{z}} \frac{1}{\pi\left(1+x^{2}\right)} d x \\ &=\frac{2}{\pi} \arctan \sqrt{z} \end{aligned} P(Z≤z)=P(−z≤Y≤z)=2∫0zπ(1+x2)1dx=π2arctanz After derivation , There's a density function
f Z ( z ) = 1 π ( 1 + z ) z , z > 0 f_{Z}(z)=\frac{1}{\pi(1+z) \sqrt{z}}, z>0 fZ(z)=π(1+z)z1,z>0 let me put it another way , because Y ∼ t ( 1 ) Y \sim t(1) Y∼t(1), so Z = Y 2 ∼ F ( 1 , 1 ) Z=Y^{2} \sim F(1,1) Z=Y2∼F(1,1).
7、 ... and 、(10 branch ) Short answer :
(1)(5 branch ) Describe the definition of sufficient statistics .
(2)(5 branch ) Narration C-R inequality .
Solution:
(1) Sufficient statistics are statistics that fully contain the information of sample characterization parameters , When sufficient statistics T T T Timing , Conditional distribution of samples f ( x 1 , ⋯ , x n ∣ T = t ) f\left(x_{1}, \cdots, x_{n} \mid T=t\right) f(x1,⋯,xn∣T=t) It has nothing to do with parameters .
(2) C-R Inequality refers to a kind of population ( Satisfy the regularity condition : Integral derivation can be ordered in a different order ) When considering the unbiased estimation of the function of parameters, the variance will have a lower bound , If yes g ( θ ) g(\theta) g(θ) Make an estimate , C-R The lower bound is [ g ′ ( θ ) ] 2 n I ( θ ) \frac{\left[g^{\prime}(\theta)\right]^{2}}{n I(\theta)} nI(θ)[g′(θ)]2, among I ( θ ) = E [ ∂ ln f ( X ; θ ) ∂ θ ] 2 I(\theta)=\mathrm{E}\left[\frac{\partial \ln f(X ; \theta)}{\partial \theta}\right]^{2} I(θ)=E[∂θ∂lnf(X;θ)]2 It's Fisher information .
8、 ... and 、(10 branch ) Some come from the general f ( x ) = 2 x , 0 < x < 1 f(x)=2x,0<x<1 f(x)=2x,0<x<1 Of 10 Random sample X 1 , ⋯ , X 10 X_1,\cdots,X_{10} X1,⋯,X10, ask X ( 3 ) X ( 6 ) \frac{X_{(3)}}{X_{(6)}} X(6)X(3) And X ( 6 ) X_{(6)} X(6) Is it independent , Please give reasons .
Solution:
( U = X ( 3 ) X ( 6 ) , V = X ( 6 ) ) \left(U=\frac{X_{(3)}}{X_{(6)}}, V=X_{(6)}\right) (U=X(6)X(3),V=X(6)) The joint distribution of is :
f ( u , v ) = v f X ( 3 ) , X ( 6 ) ( u v , v ) = C v 10 ( 1 − v 2 ) 4 u 5 ( 1 − u 2 ) 2 \begin{aligned} f(u, v) &=v f_{X_{(3)}, X_{(6)}}(u v, v) \\ &=C v^{10}\left(1-v^{2}\right)^{4} u^{5}\left(1-u^{2}\right)^{2} \end{aligned} f(u,v)=vfX(3),X(6)(uv,v)=Cv10(1−v2)4u5(1−u2)2 among , u ∈ ( 0 , 1 ) , v ∈ ( 0 , 1 ) u \in(0,1), v \in(0,1) u∈(0,1),v∈(0,1), The definition field is rectangular and can be factorized , so U , V U, V U,V Independent .
Nine 、(10 branch ) Some come from the general N ( μ , 1 ) N(\mu,1) N(μ,1) Of n n n Random sample X 1 , ⋯ , X n X_1,\cdots,X_n X1,⋯,Xn, prove : X ˉ \bar{X} Xˉ It's full statistics .
Solution:
The joint density function can be written as
f ( x 1 , ⋯ , x n ; μ ) = C exp { − ∑ i = 1 n ( x i − μ ) 2 2 } = C exp { − − 2 μ ∑ i = 1 n x i + n μ 2 + ∑ i = 1 n x i 2 2 } \begin{aligned} f\left(x_{1}, \cdots, x_{n} ; \mu\right) &=C \exp \left\{-\frac{\sum_{i=1}^{n}\left(x_{i}-\mu\right)^{2}}{2}\right\} \\ &=C \exp \left\{-\frac{-2 \mu \sum_{i=1}^{n} x_{i}+n \mu^{2}+\sum_{i=1}^{n} x_{i}^{2}}{2}\right\} \end{aligned} f(x1,⋯,xn;μ)=Cexp{ −2∑i=1n(xi−μ)2}=Cexp{ −2−2μ∑i=1nxi+nμ2+∑i=1nxi2} By the Factorization Theorem , X ˉ \bar{X} Xˉ It's full statistics .
Ten 、(10 branch ) Some come from the general U ( θ , 2 θ ) U(\theta,2\theta) U(θ,2θ) Of n n n Random sample X 1 , ⋯ , X n X_1,\cdots,X_n X1,⋯,Xn, seek θ \theta θ Maximum likelihood estimation of , And judge its unbiasedness and consistency .
Solution:
The likelihood function is
L ( θ ) = 1 θ n I { x ( 1 ) > θ > x ( w ) 2 } , L(\theta)=\frac{1}{\theta^{n}} I_{\left\{x_{(1)}>\theta>\frac{x_{(w)}}{2}\right\}}, L(θ)=θn1I{ x(1)>θ>2x(w)}, The previous part is about θ \theta θ Monotonic decline , Description of indicative function θ \theta θ The minimum is x ( n ) 2 \frac{x_{(n)}}{2} 2x(n), So the maximum likelihood estimation is θ ^ = X ( n ) 2 \hat{\theta}=\frac{X_{(n)}}{2} θ^=2X(n). Make Y = X − θ θ ∼ U ( 0 , 1 ) Y=\frac{X-\theta}{\theta} \sim U(0,1) Y=θX−θ∼U(0,1), so E Y ( n ) = n n + 1 , E Y ( n ) * a.s. 1 \mathrm{E} Y_{(n)}=\frac{n}{n+1}, \mathrm{E} Y_{(n)} \stackrel{\text { a.s. }}{\longrightarrow} 1 EY(n)=n+1n,EY(n)* a.s. 1, There are
E θ ^ = 2 n + 1 2 n + 2 θ ≠ θ , θ ^ * a.s. θ . \mathrm{E} \hat{\theta}=\frac{2 n+1}{2 n+2} \theta \neq \theta, \hat{\theta} \stackrel{\text { a.s. }}{\longrightarrow} \theta \text {. } Eθ^=2n+22n+1θ=θ,θ^* a.s. θ.
11、 ... and 、(10 branch ) Some come from the general N ( μ , σ 2 ) N(\mu,\sigma^2) N(μ,σ2) Of n n n Random sample X 1 , ⋯ , X n X_1,\cdots,X_n X1,⋯,Xn, among μ \mu μ It is known that , Make
σ ^ = 1 n π 2 ∑ i = 1 n ∣ X i − μ ∣ , \hat{\sigma}=\frac{1}{n}\sqrt{\frac{\pi}{2}}\sum_{i=1}^n{\left| X_i-\mu \right|}, σ^=n12πi=1∑n∣Xi−μ∣, verification σ ^ \hat{\sigma} σ^ yes σ \sigma σ Unbiased estimation of , But it is not an effective estimate .
Solution:
To calculate σ 2 \sigma^{2} σ2 Of Fisher The amount of information , According to the definition
I ( σ 2 ) = E [ ∂ ln f ( X ; σ 2 ) ∂ σ 2 ] 2 = 1 4 σ 4 E [ ( X − μ σ ) 2 − 1 ] 2 , I\left(\sigma^{2}\right)=E\left[\frac{\partial \ln f\left(X ; \sigma^{2}\right)}{\partial \sigma^{2}}\right]^{2}=\frac{1}{4 \sigma^{4}} E\left[\left(\frac{X-\mu}{\sigma}\right)^{2}-1\right]^{2}, I(σ2)=E[∂σ2∂lnf(X;σ2)]2=4σ41E[(σX−μ)2−1]2, just E [ ( X − μ σ ) 2 − 1 ] 2 E\left[\left(\frac{X-\mu}{\sigma}\right)^{2}-1\right]^{2} E[(σX−μ)2−1]2 yes χ 2 ( 1 ) \chi^{2}(1) χ2(1) The variance of , so I ( σ 2 ) = 1 2 σ 4 I\left(\sigma^{2}\right)=\frac{1}{2 \sigma^{4}} I(σ2)=2σ41. Make g ( x ) = x g(x)=\sqrt{x} g(x)=x, be σ \sigma σ Of C-R The lower bound is [ g ′ ( σ 2 ) ] 2 n I ( σ 2 ) = 1 2 n σ 2 \frac{\left[g^{\prime}\left(\sigma^{2}\right)\right]^{2}}{n I\left(\sigma^{2}\right)}=\frac{1}{2 n} \sigma^{2} nI(σ2)[g′(σ2)]2=2n1σ2, Let's calculate 1 n π 2 ∑ i = 1 n ∣ X i − μ ∣ \frac{1}{n} \sqrt{\frac{\pi}{2}} \sum_{i=1}^{n}\left|X_{i}-\mu\right| n12π∑i=1n∣Xi−μ∣ The expected variance of :
1 σ E ∣ X 1 − μ ∣ = ∫ − ∞ + ∞ ∣ x ∣ 1 2 π e − x 2 2 d x = 2 π ∫ 0 + ∞ x e − x 2 2 d x = 2 π ⇒ E ∣ X 1 − μ ∣ = 2 π σ , E ∣ X 1 − μ ∣ 2 = σ 2 , so Var ( ∣ X 1 − μ ∣ ) = σ 2 − 2 π σ 2 = ( 1 − 2 π ) σ 2 , \begin{gathered} \frac{1}{\sigma} E\left|X_{1}-\mu\right|=\int_{-\infty}^{+\infty}|x| \frac{1}{\sqrt{2 \pi}} e^{-\frac{x^{2}}{2}} d x=\sqrt{\frac{2}{\pi}} \int_{0}^{+\infty} x e^{-\frac{x^{2}}{2}} d x=\sqrt{\frac{2}{\pi}} \Rightarrow E\left|X_{1}-\mu\right|=\sqrt{\frac{2}{\pi}} \sigma, \\ E\left|X_{1}-\mu\right|^{2}=\sigma^{2}, \text { so } \operatorname{Var}\left(\left|X_{1}-\mu\right|\right)=\sigma^{2}-\frac{2}{\pi} \sigma^{2}=\left(1-\frac{2}{\pi}\right) \sigma^{2}, \end{gathered} σ1E∣X1−μ∣=∫−∞+∞∣x∣2π1e−2x2dx=π2∫0+∞xe−2x2dx=π2⇒E∣X1−μ∣=π2σ,E∣X1−μ∣2=σ2, so Var(∣X1−μ∣)=σ2−π2σ2=(1−π2)σ2, so E [ 1 n π 2 ∑ i = 1 n ∣ X i − μ ∣ ] = σ , Var [ 1 n π 2 ∑ i = 1 n ∣ X i − μ ∣ ] = ( π 2 − 1 ) n σ 2 , E\left[\frac{1}{n} \sqrt{\frac{\pi}{2}} \sum_{i=1}^{n}\left|X_{i}-\mu\right|\right]=\sigma, \operatorname{Var}\left[\frac{1}{n} \sqrt{\frac{\pi}{2}} \sum_{i=1}^{n}\left|X_{i}-\mu\right|\right]=\frac{\left(\frac{\pi}{2}-1\right)}{n} \sigma^{2}, E[n12πi=1∑n∣Xi−μ∣]=σ,Var[n12πi=1∑n∣Xi−μ∣]=n(2π−1)σ2, It is an unbiased estimate , But it didn't reach C-R Lower bound , Not a valid estimate .
Twelve 、(10 branch ) Some come from the general P ( θ ) \mathcal P(\theta) P(θ) Of n n n Random sample , Consider the hypothesis test problem :
H 0 : θ = 2 v s H 1 : θ = 3 , \mathrm{H}_0:\theta=2 \quad \mathrm{vs} \quad \mathrm{H}_1:\theta=3, H0:θ=2vsH1:θ=3, There are denial domains W = { x ˉ ≥ 2.8 } W=\{ \bar{x} \ge 2.8\} W={ xˉ≥2.8}, ask
(1)(5 branch ) n = 5 n=5 n=5 when , What is the probability of making two kinds of mistakes ?
(2)(5 branch ) n n n Towards infinity , What happens to the probability of making two kinds of mistakes ? Please explain .
Solution:
(1) The first type of error is :
α = P θ = 2 { X ˉ ≥ 2.8 } = P θ = 2 { ∑ i = 1 5 X i ≥ 14 } = ∑ k = 14 ∞ 1 0 k k ! e − 10 \begin{aligned} \alpha &=\mathrm{P}_{\theta=2}\{\bar{X} \geq 2.8\} \\ &=\mathrm{P}_{\theta=2}\left\{\sum_{i=1}^{5} X_{i} \geq 14\right\} \\ &=\sum_{k=14}^{\infty} \frac{10^{k}}{k !} e^{-10} \end{aligned} α=Pθ=2{ Xˉ≥2.8}=Pθ=2{ i=1∑5Xi≥14}=k=14∑∞k!10ke−10 The second type of error is :
β = P θ = 3 { X ˉ < 2.8 } = P θ = 3 { ∑ i = 1 5 X i < 14 } = ∑ k = 0 13 1 5 k k ! e − 15 \begin{aligned} \beta &=\mathrm{P}_{\theta=3}\{\bar{X}<2.8\} \\ &=\mathrm{P}_{\theta=3}\left\{\sum_{i=1}^{5} X_{i}<14\right\} \\ &=\sum_{k=0}^{13} \frac{15^{k}}{k !} e^{-15} \end{aligned} β=Pθ=3{ Xˉ<2.8}=Pθ=3{ i=1∑5Xi<14}=k=0∑13k!15ke−15(2) From the law of large numbers :
α = P θ = 2 { X ˉ ≥ 2.8 } ≤ P θ = 2 { ∣ X ˉ − 2 ∣ ≥ 0.8 } * 0 β = P θ = 3 { X ˉ < 2.8 } ≤ P θ = 3 { ∣ X ˉ − 3 ∣ > 0.2 } * 0 \begin{aligned} \alpha &=\mathrm{P}_{\theta=2}\{\bar{X} \geq 2.8\} \\ & \leq \mathrm{P}_{\theta=2}\{|\bar{X}-2| \geq 0.8\} \longrightarrow 0 \\ \beta &=\mathrm{P}_{\theta=3}\{\bar{X}<2.8\} \\ & \leq \mathrm{P}_{\theta=3}\{|\bar{X}-3|>0.2\} \longrightarrow 0 \end{aligned} αβ=Pθ=2{ Xˉ≥2.8}≤Pθ=2{ ∣Xˉ−2∣≥0.8}*0=Pθ=3{ Xˉ<2.8}≤Pθ=3{ ∣Xˉ−3∣>0.2}*0 So when the sample size tends to infinity , Both types of errors tend to 0 .
边栏推荐
- System design learning (III) design Amazon's sales rank by category feature
- [中国近代史] 第六章测验
- Redis的两种持久化机制RDB和AOF的原理和优缺点
- 西安电子科技大学22学年上学期《基础实验》试题及答案
- 【九阳神功】2021复旦大学应用统计真题+解析
- IPv6 experiment
- Solution: warning:tensorflow:gradients do not exist for variables ['deny_1/kernel:0', 'deny_1/bias:0',
- Data manipulation language (DML)
- View UI Plus 发布 1.1.0 版本,支持 SSR、支持 Nuxt、增加 TS 声明文件
- 最新坦克大战2022-全程开发笔记-3
猜你喜欢
The latest tank battle 2022 - Notes on the whole development -2
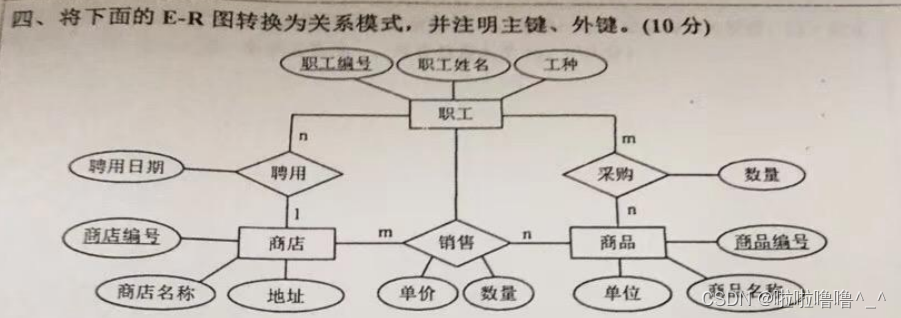
TYUT太原理工大学2022数据库大题之E-R图转关系模式
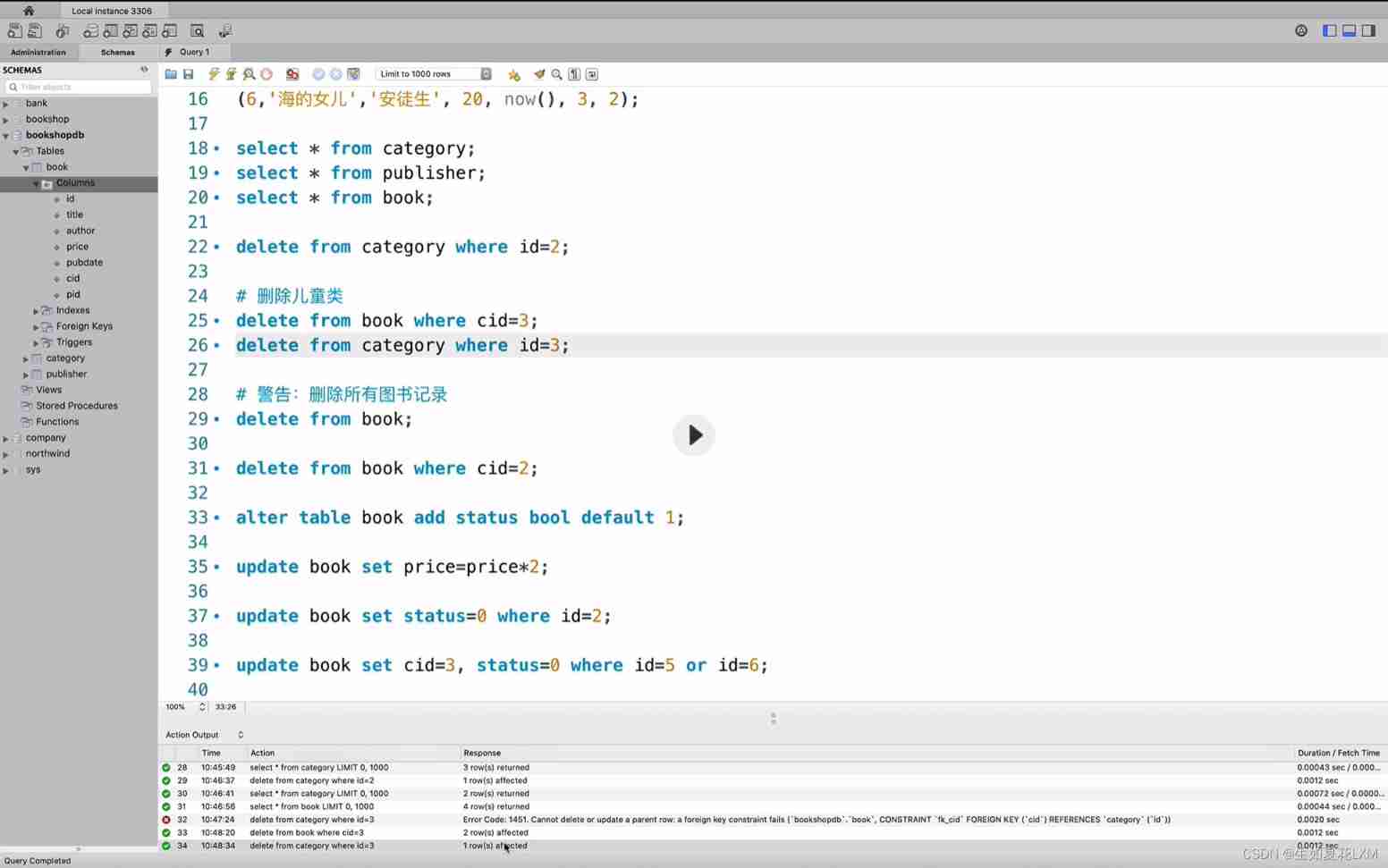
Data manipulation language (DML)
20220211-CTF-MISC-006-pure_ Color (use of stegsolve tool) -007 Aesop_ Secret (AES decryption)

7. Relationship between array, pointer and array
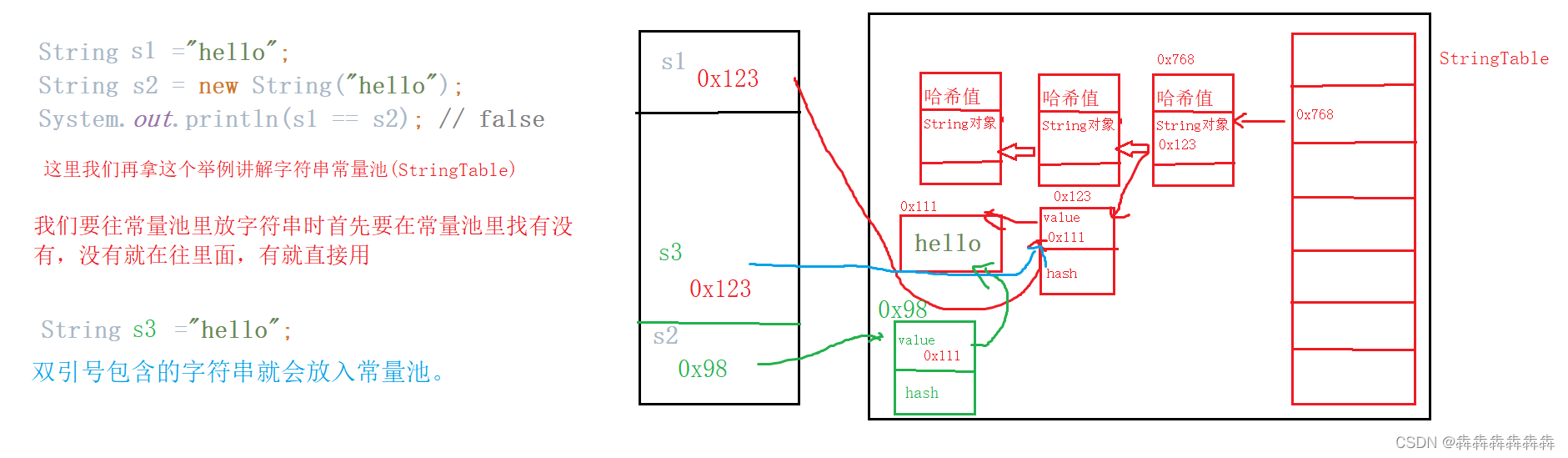
String class

Quickly generate illustrations
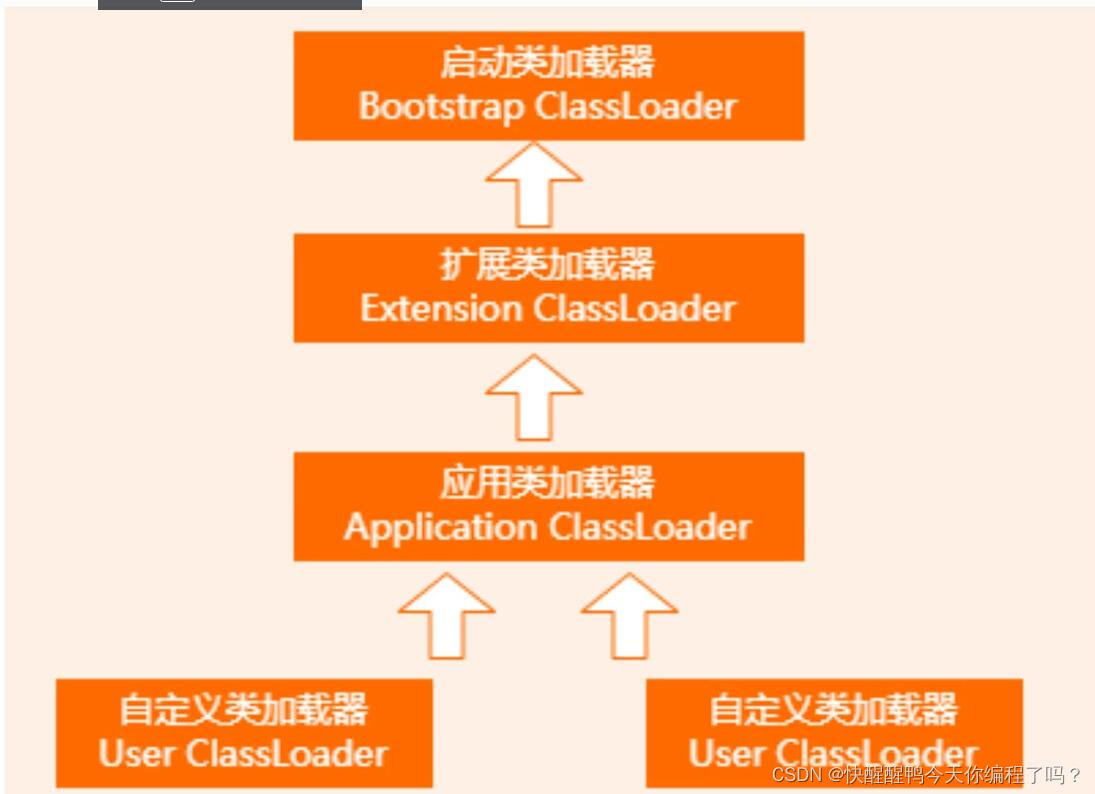
关于双亲委派机制和类加载的过程
C language Getting Started Guide
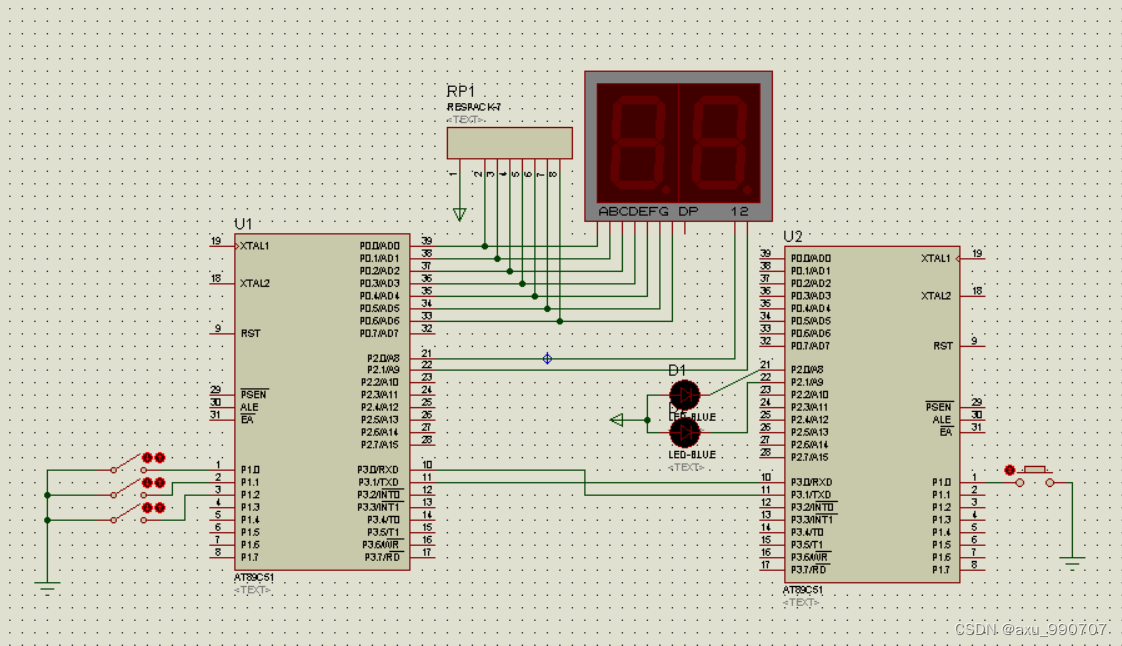
甲、乙机之间采用方式 1 双向串行通信,具体要求如下: (1)甲机的 k1 按键可通过串行口控制乙机的 LEDI 点亮、LED2 灭,甲机的 k2 按键控制 乙机的 LED1
随机推荐
3.猜数字游戏
vector
TYUT太原理工大学2022数据库大题之概念模型设计
View UI Plus 发布 1.3.1 版本,增强 TypeScript 使用体验
String abc = new String(“abc“),到底创建了几个对象
Change vs theme and set background picture
六种集合的遍历方式总结(List Set Map Queue Deque Stack)
Floating point comparison, CMP, tabulation ideas
1.初识C语言(1)
C language Getting Started Guide
Rich Shenzhen people and renting Shenzhen people
3.C语言用代数余子式计算行列式
3. Number guessing game
Alibaba cloud microservices (I) service registry Nacos, rest template and feign client
List set map queue deque stack
arduino+DS18B20温度传感器(蜂鸣器报警)+LCD1602显示(IIC驱动)
【快趁你舍友打游戏,来看道题吧】
Redis cache obsolescence strategy
12 excel charts and arrays
凡人修仙学指针-1