当前位置:网站首页>中国剩余定理 AcWing 204. 表达整数的奇怪方式
中国剩余定理 AcWing 204. 表达整数的奇怪方式
2022-07-05 06:16:00 【T_Y_F666】
中国剩余定理 AcWing 204. 表达整数的奇怪方式
原题链接
算法标签
数学知识 同余方程 扩展中国剩余定理
思路
代码
#include<bits/stdc++.h>
#define int long long
#define abs fabs
#define rep(i, a, b) for(int i=a;i<b;++i)
#define Rep(i, a, b) for(int i=a;i>=b;--i)
using namespace std;
const int N = 105;
int a[N][N], eps = 1e-8;
int n;
inline int read(){
int s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
void put(int x) {
if(x<0) putchar('-'),x=-x;
if(x>=10) put(x/10);
putchar(x%10^48);
}
int exgcd(int a, int b, int &x, int &y){
if(!b){
x=1, y=0;
return a;
}else{
int d=exgcd(b, a%b, y, x);
y-=a/b*x;
return d;
}
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
n=read();
int x=0, m1=read(), a1=read();
rep(i, 0, n-1){
int m2=read(), a2=read();
int k1, k2;
int d=exgcd(m1, m2, k1, k2);
if((a2-a1)%d){
x=-1;
break;
}
k1*=(a2-a1)/d;
k1=(k1 % (m2/d) + m2/d) % (m2/d);
x=k1*m1+a1;
int m=abs(m1/d*m2);
a1=k1*m1+a1;
m1=m;
}
if(x!=-1){
x = (a1 % m1 + m1) % m1;
}
printf("%lld",x);
return 0;
}
原创不易
转载请标明出处
如果对你有所帮助 别忘啦点赞支持哈
边栏推荐
猜你喜欢
wordpress切换页面,域名变回了IP地址
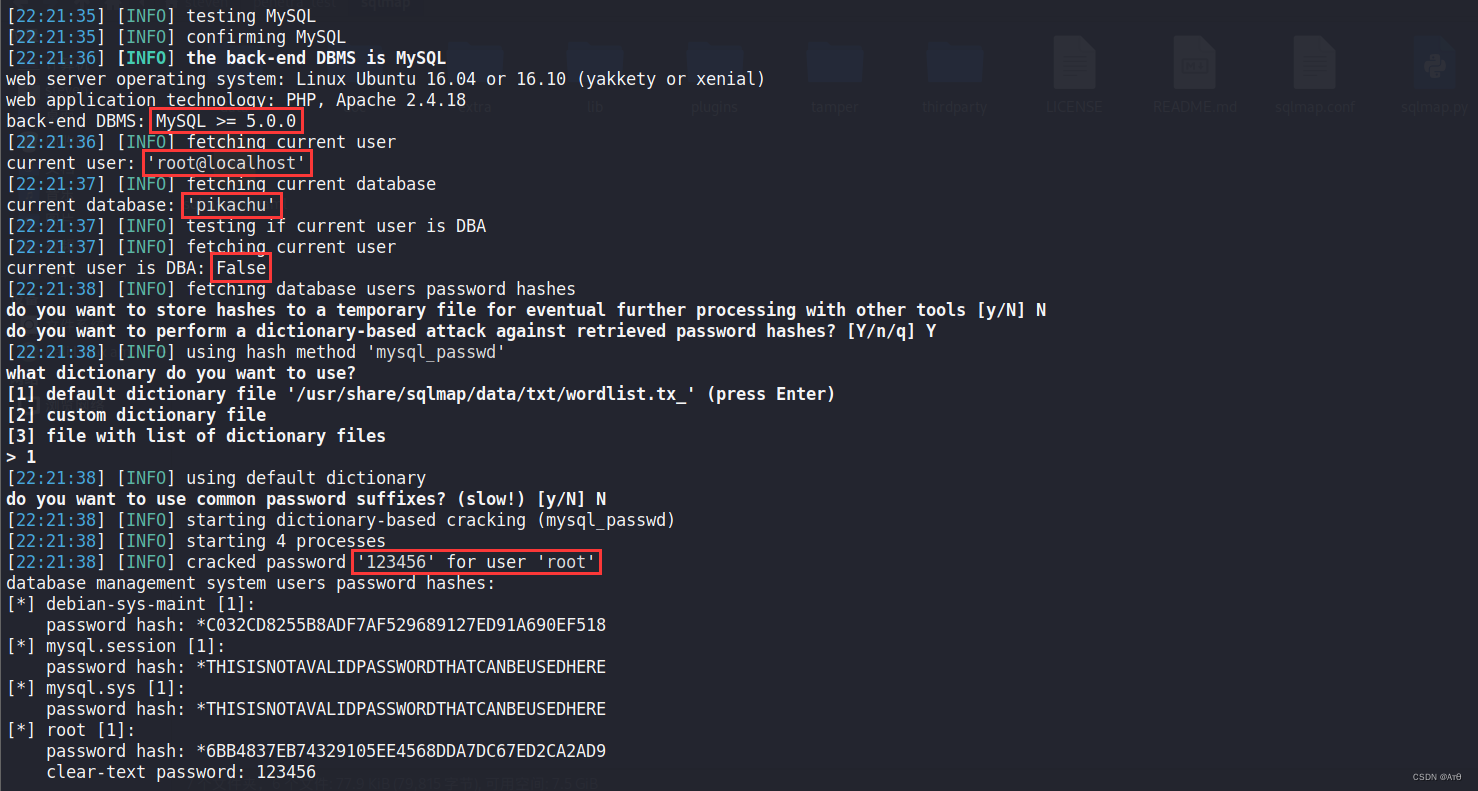
Sqlmap tutorial (II) practical skills I

1.15 - 输入输出系统

Simple selection sort of selection sort

Liunx starts redis
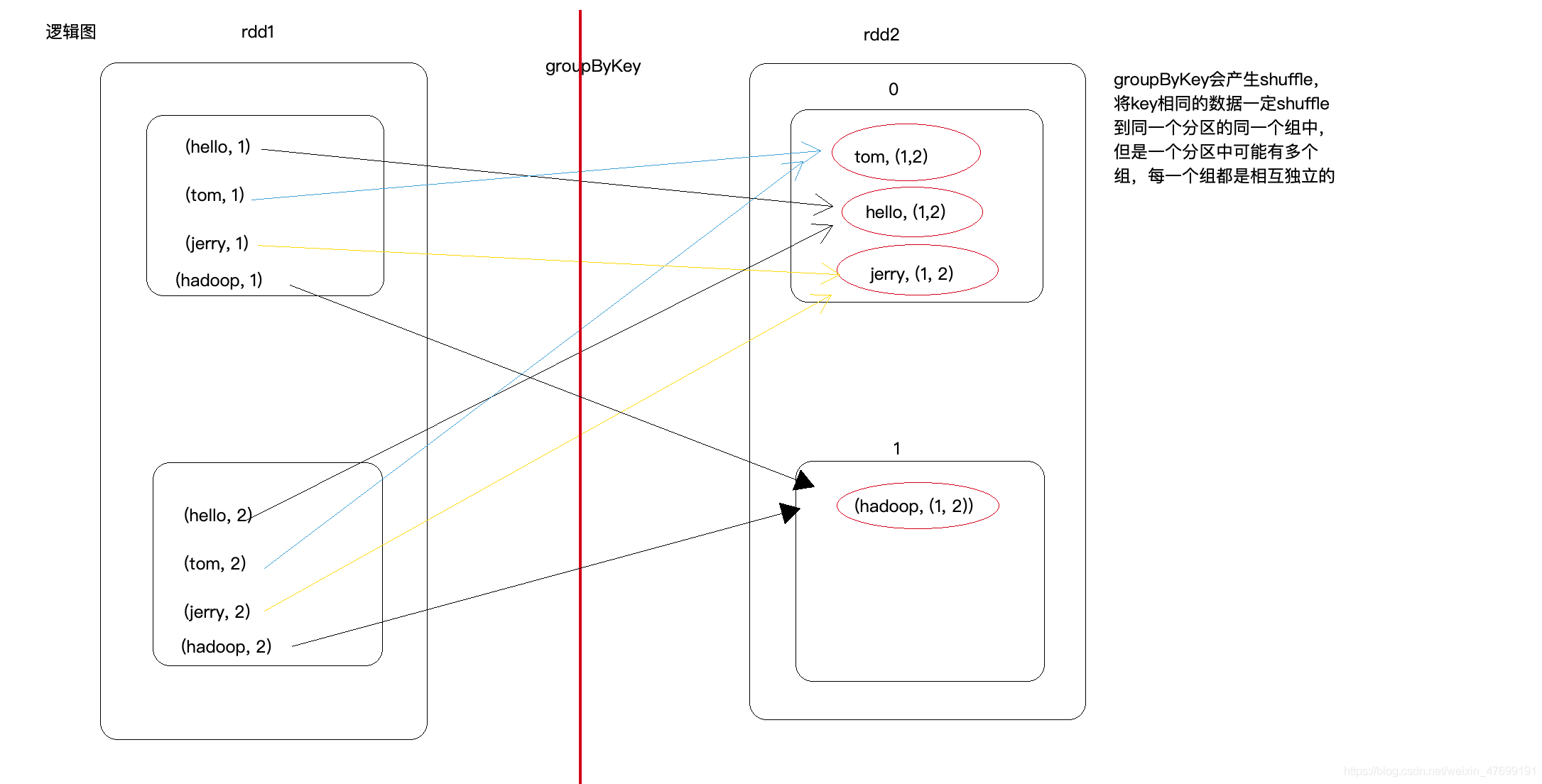
Groupbykey() and reducebykey() and combinebykey() in spark

4. Object mapping Mapster
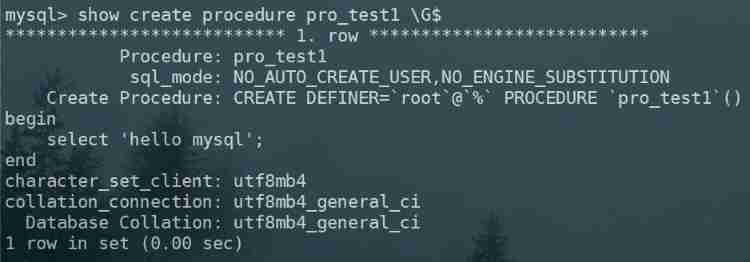
MySQL advanced part 1: stored procedures and functions

Doing SQL performance optimization is really eye-catching

1.15 - input and output system
随机推荐
SPI details
可变电阻器概述——结构、工作和不同应用
Simple selection sort of selection sort
Leetcode backtracking method
MySQL advanced part 1: stored procedures and functions
[BMZCTF-pwn] ectf-2014 seddit
Sum of three terms (construction)
Leetcode-22: bracket generation
leetcode-556:下一个更大元素 III
【Rust 笔记】17-并发(上)
LeetCode 1200. Minimum absolute difference
One question per day 1020 Number of enclaves
1.15 - input and output system
Operator priority, one catch, no doubt
SQLMAP使用教程(一)
LaMDA 不可能觉醒吗?
2021apmcm post game Summary - edge detection
多屏电脑截屏会把多屏连着截下来,而不是只截当前屏
SQLMAP使用教程(二)实战技巧一
[rust notes] 17 concurrent (Part 1)



