当前位置:网站首页>Sum of three terms (construction)
Sum of three terms (construction)
2022-07-05 06:16:00 【whitewall_ nine】
https://atcoder.jp/contests/arc135/tasks
#include<iostream>
#include<map>
#include<cstring>
using namespace std;
#define rep(i,l,r) for(int i=(l);i<=(r);i++)
#define per(i,l,r) for(int i=(l);i>=(r);i--)
#define ll long long
#define pii pair<int, int>
#define mset(s,t) memset(s,t,sizeof(t))
#define mcpy(s,t) memcpy(s,t,sizeof(t))
#define fir first
#define pb push_back
#define sec second
#define sortall(x) sort((x).begin(),(x).end())
inline int read () {
int x = 0, f = 0;
char ch = getchar();
while (!isdigit(ch)) f |= (ch=='-'),ch= getchar();
while (isdigit(ch)) x = x * 10 + ch - '0', ch = getchar();
return f?-x:x;
}
template<typename T> void print(T x) {
if (x < 0) putchar('-'), x = -x;
if (x >= 10) print(x/10);
putchar(x % 10 + '0');
}
const int mod = 998244353;
const int N = 3e5 + 10;
int a[N];
int s[N];
int n;
void solve() {
cin >> n;
for (int i = 0; i< n; i ++) cin >> a[i];
int minvy = 0, minvx = 0;
// Negative numbers need not be considered , Because he was a positive number , It must be greater than or equal to 0 Conditions , Then we just need to find the smallest negative number
int maxx = 0x3f3f3f3f;
for (int i = 2; i< n + 2; i ++) {
s[i] = a[i - 2] - s[i - 1] - s[i - 2];
if (i % 3 == 0) {
minvy = max (minvy, -s[i]);
}
else if (i % 3 == 1) {
minvx = max(minvx, -s[i]);
}
else {
maxx = min(maxx, s[i]);
}
}
if (minvy + minvx > maxx) {
puts("No");
return ;
}
puts("Yes");
s[0] = minvy, s[1] = minvx;
for (int i = 2; i < n + 2; i ++)
s[i] = a[i - 2] - s[i - 1] - s[i - 2];
for (int i = 0; i < n + 2; i ++)
cout << s[i] << " \n"[i == n + 1];
}
int main () {
int t;
t = 1;
while (t --) solve();
return 0;
}
This problem is solved by finding the boundary range and then constructing a feasible solution . By simplifying the formula You can find i % 3 == 0 s[i] = x +a i % 3 == 1 s[i] = x + b i % 3== 2 s[i] = x - a - b We need to find out whether the limit conditions are feasible To this end, we construct c1, c2, c3 c1 <= a c2 <= b a + b <=c3 c1 + c2<= a + b <= c3 Maximum left , Take the minimum on the right and judge whether it meets the size relationship to judge whether it is feasible . If it is satisfied, just substitute the value directly
边栏推荐
- 1041 Be Unique
- Daily question 1984 Minimum difference in student scores
- LeetCode 0107.二叉树的层序遍历II - 另一种方法
- 做 SQL 性能优化真是让人干瞪眼
- The connection and solution between the shortest Hamilton path and the traveling salesman problem
- 数据可视化图表总结(一)
- Regulations for network security events of vocational group in 2022 Guizhou Vocational College skill competition
- 1996. number of weak characters in the game
- 927. Trisection simulation
- Dynamic planning solution ideas and summary (30000 words)
猜你喜欢
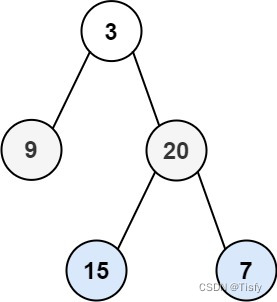
LeetCode 0107. Sequence traversal of binary tree II - another method
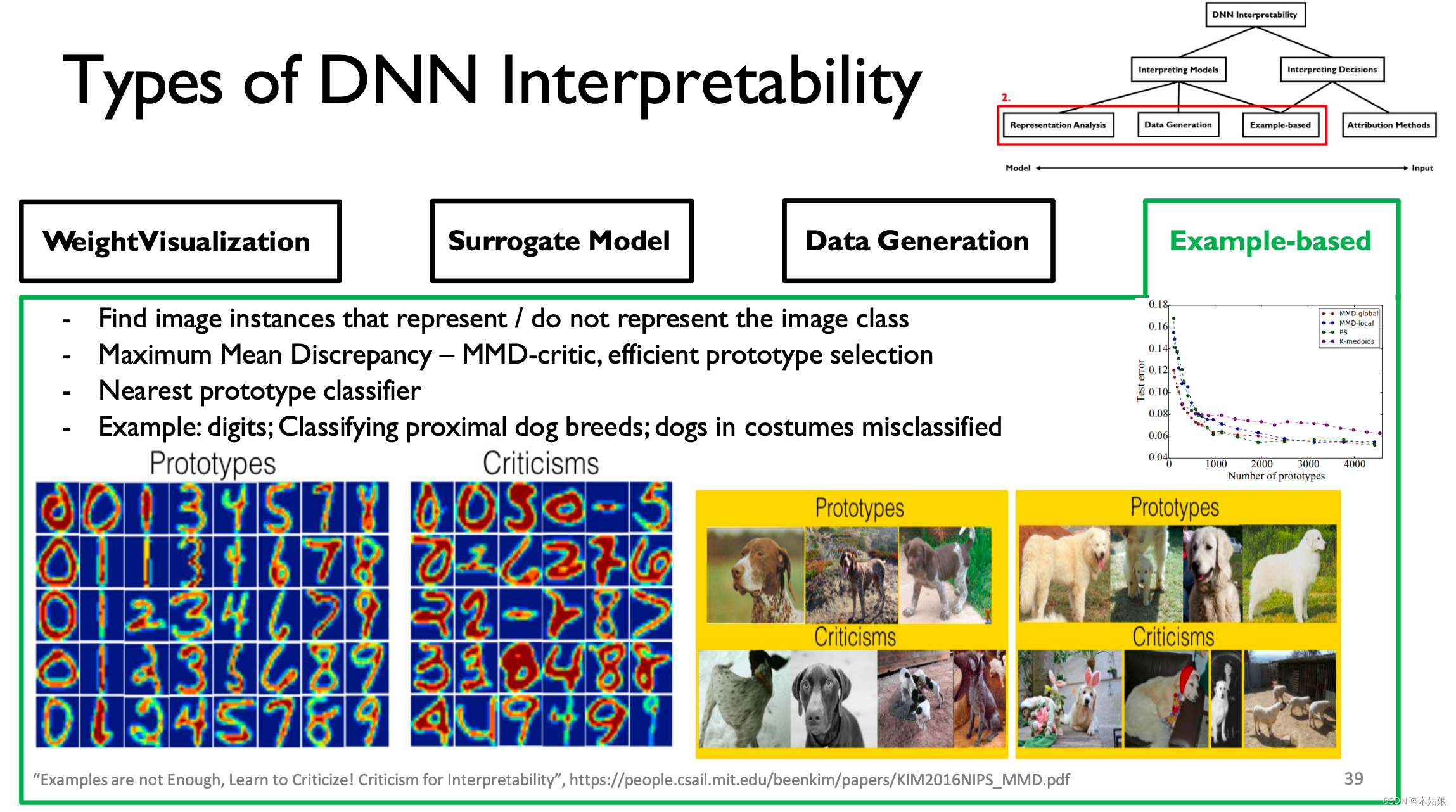
MIT-6874-Deep Learning in the Life Sciences Week 7
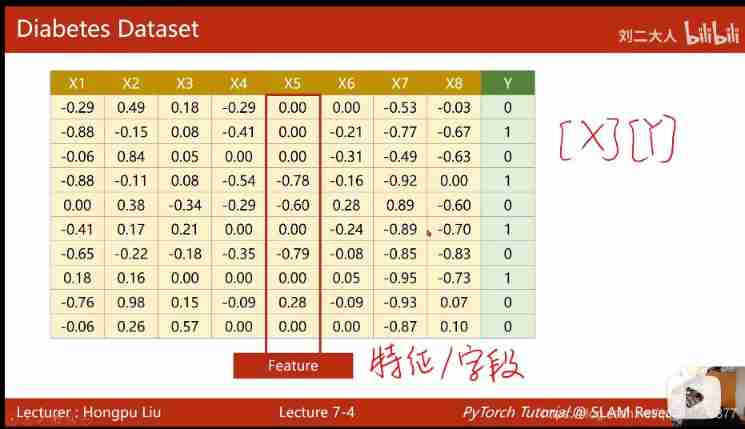
7. Processing the input of multidimensional features
![Introduction to LVS [unfinished (semi-finished products)]](/img/72/d5a943a8d6d71823dcbd7f23dda35b.png)
Introduction to LVS [unfinished (semi-finished products)]
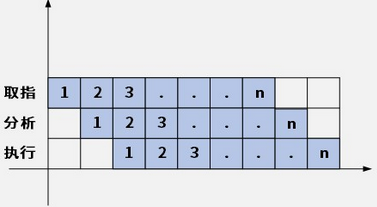
1.14 - assembly line
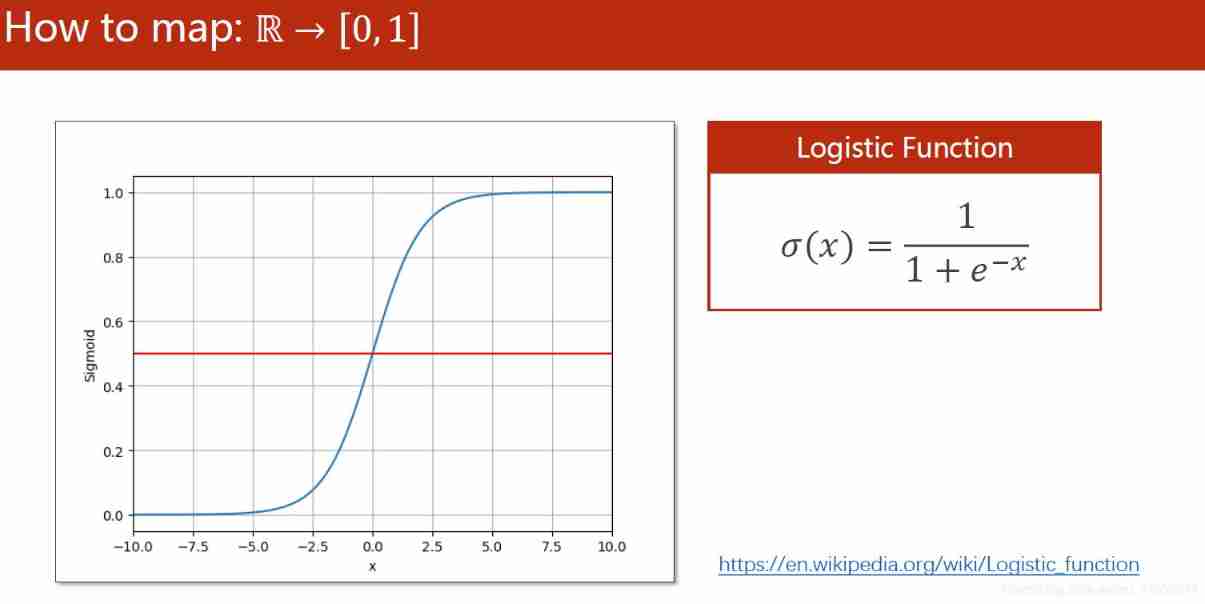
6. Logistic model
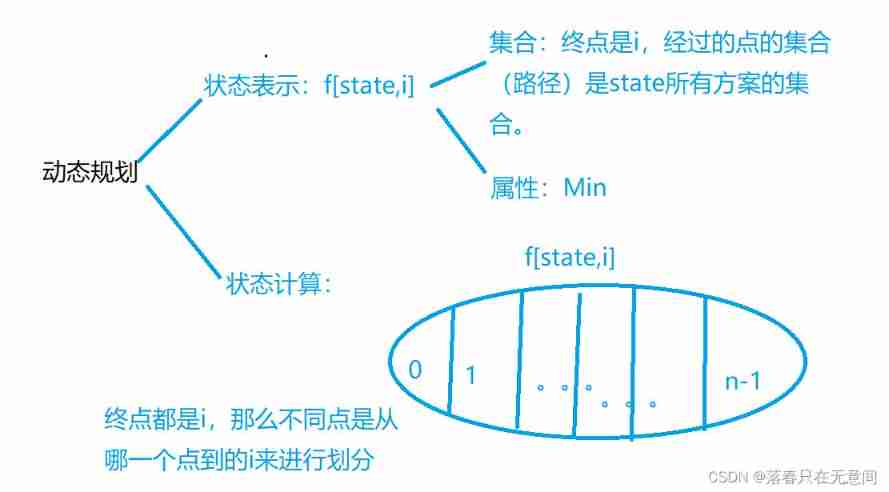
The connection and solution between the shortest Hamilton path and the traveling salesman problem
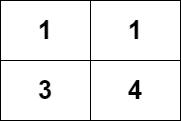
leetcode-6110:网格图中递增路径的数目
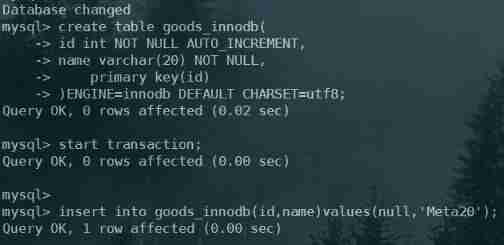
MySQL advanced part 2: storage engine
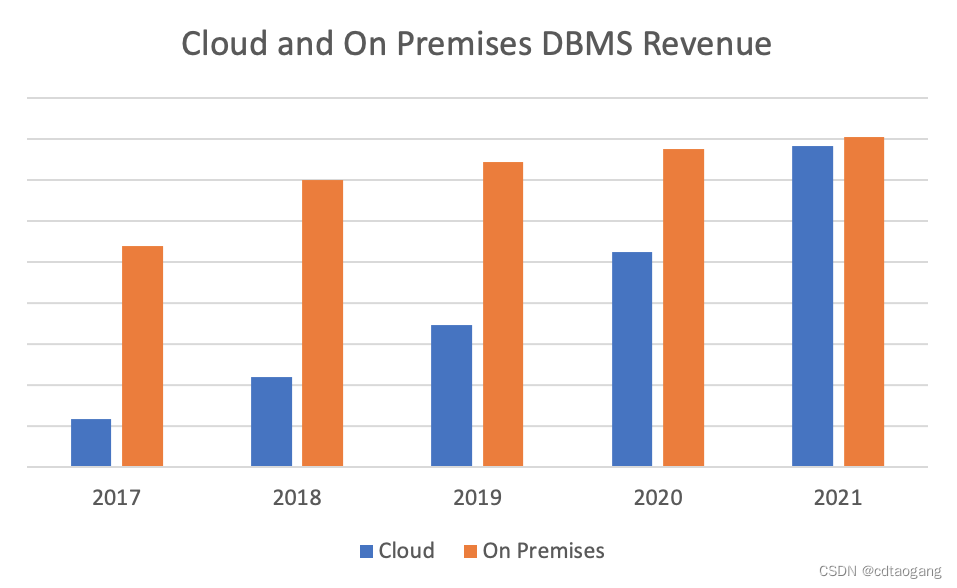
传统数据库逐渐“难适应”,云原生数据库脱颖而出
随机推荐
leetcode-31:下一个排列
QQ computer version cancels escape character input expression
一些工具的记录2022
SQLMAP使用教程(二)实战技巧一
6. Logistic model
Leetcode heap correlation
How to adjust bugs in general projects ----- take you through the whole process by hand
Leetcode dynamic programming
Shutter web hardware keyboard monitoring
Leetcode-6108: decrypt messages
【Rust 笔记】13-迭代器(下)
【Rust 笔记】17-并发(下)
【LeetCode】Easy | 20. Valid parentheses
redis发布订阅命令行实现
2022年貴州省職業院校技能大賽中職組網絡安全賽項規程
RGB LED infinite mirror controlled by Arduino
Smart construction site "hydropower energy consumption online monitoring system"
对for(var i = 0;i < 5;i++) {setTimeout(() => console.log(i),1000)}的深入分析
[leetcode] day94 reshape matrix
Leetcode-6110: number of incremental paths in the grid graph