当前位置：网站首页>Dynamic planning solution ideas and summary (30000 words)

Dynamic planning solution ideas and summary (30000 words)

2022-07-05 05:41:00 【Falling spring is only inadvertently】

Preface

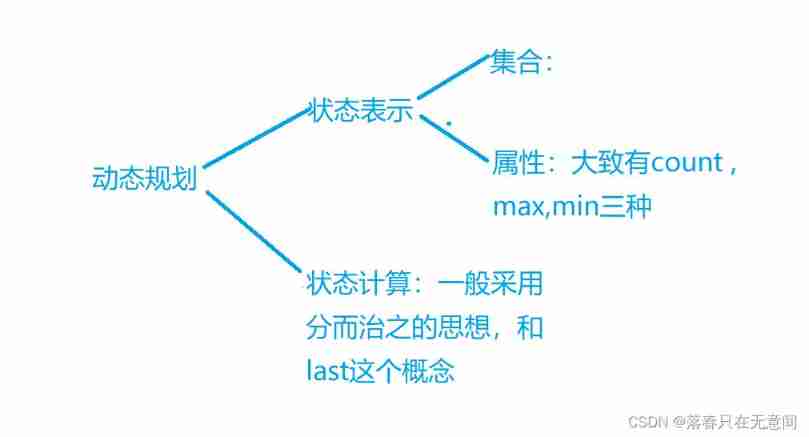
Basis of this article y General method , Use the frame force of the set to try to explain well dp Why .
The whole frame is ：

How to write dynamic planning hand in hand

The first point must be experience , After writing a certain number of topics, you can know why it is in Dynamic Planning .
The difficulty is the calculation of dynamic programming. The difficulty is the calculation of state . Dynamic programming is a special shortest path problem ( On a complementary graph ). Consider the calculation of states from the perspective of graph theory , In fact, that is , The transition relationship between different states （ There is a relationship with the edge ）

Transformation relations generally fall into two categories ：
Update the current state with the state it depends on .（80%）
Update the state that depends on it with the current state .
To draw a picture is
These two are actually equivalent .

The following two topics will explain

The longest path

Title Transfer door

First, we can write the expression of dynamic programming ( A lot of experience ),dp[i] Express y To the node i The longest path length at the end . So how do we update it , First of all, what is the previous state of this point? I don't know , But we can well know the situation of the next point pointed by this point , Is the path length of the point +1,（ This is the second case in the above figure ）, We can update the state that depends on it with the current state .
So what is the order of update ? Directed acyclic graph with title , Then we can update according to the topological order .

Code ：

#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>
using namespace std;
const int N = 2e5 + 10;
int n, m, cnt;
int h[N], ne[N], e[N], in[N];
int f[N];

void add(int u, int v) {
    
	e[++cnt] = v, ne[cnt] = h[u], h[u] = cnt;
}

void tosort() {
    
	queue<int>q;
	for (int i = 1; i <= n; ++i)
		if (!in[i])
			q.push(i);

	while (q.size()) {
    
		int u = q.front();
		q.pop();
		for (int i = h[u] ; ~i ; i = ne[i]) {
    
			int v = e[i];
			f[v] = max(f[v], f[u] + 1);
			if (--in[v] == 0)
				q.push(v);
		}
	}
}

int main() {
    
	cin >> n >> m;
	memset(h, -1, sizeof h);
	while (m--) {
    
		int a, b;
		cin >> a >> b;
		add(a, b);
		in[b]++;
	}
	tosort();
	int res = 0;
	for (int i = 1 ; i <= n ; ++i)
		res = max(res, f[i]);
	cout << res << endl;
	return 0;
}

grid

Title Transfer door
The above question is the second kind of situation , Then let's talk about the first kind of situation ;

First, we define the state of dynamic programming as ：dp[i][j] : From (1,1) To (i,j) Number of paths for .
From the meaning of the title , For each of these dp[i][j] , He can only come from the top or left , So for each dp[i][j] Add the number of paths in these two directions .

Code ：

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1010, mod = 1e9 + 7 ;
int n, m ;
char g[N][N];
int f[N][N];


int dx[2] = {
    -1, 0}, dy[2] = {
    0, -1};

int main() {
    
	cin >> n >> m;
	for (int i = 0 ; i < n ; ++i)
		cin >> g[i];
	f[0][0] = 1;
	for (int i = 0 ; i < n ; ++i)
		for (int j = 0 ; j < m ; ++j) {
    
			if (g[i][j] == '#')
				continue;
			for (int k = 0 ; k < 2 ; ++k) {
    
				int xx = i + dx[k], yy = j + dy[k];
				if (xx < 0 || xx >= n || yy < 0 || yy >= m)
					continue;
				if (g[xx ][yy ] == '.')
					f[i][j] = (f[i][j] + f[xx][yy]) % mod;
			}
		}
	cout << f[n - 1][m - 1] << endl;
	return 0;
}

The longest ascending subsequence problem

Find the longest ascending subsequence

First of all, let's write some ideas according to the framework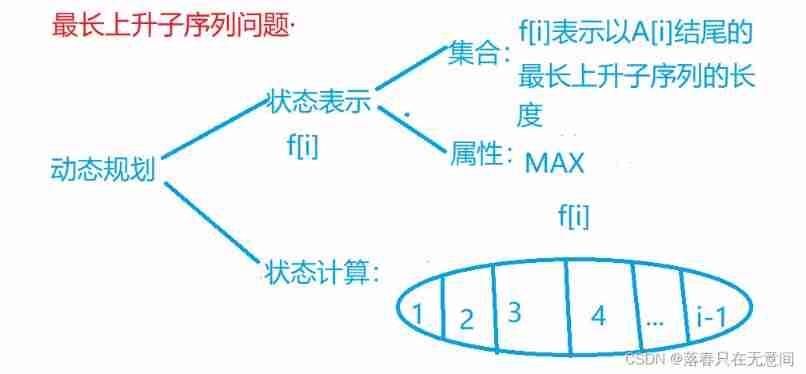
Insert picture description here

Let's talk about why the state calculation is divided into this .f[i] In order to A[I] Is the maximum of all cases at the end . Then let's introduce last The concept , For all with A[i] Ascending sequence at the end , Because the last one is A[i] Then the difference between them is to get rid of A[I] The first number after , That is, the penultimate number . So we all get rid of A[i] And to enumerate the previous satisfaction , And meaningful can know these are f[1~(i-1] The definition of . So we enumerate from 1~（i-1） Meet the rising . Taking the maximum .
Core code

for(int i = 2 ; i <= n ;++i){
    
	for(int j =  1 ; j < i ; ++j )
		if(a[i] > a[j]) f[i] = max(f[i] , f[j] + 1);
}

The above method is obviously $O(n^2)$ It's a way of thinking . Obviously not acceptable . So let's see how to optimize ？ The repeated calculation is mainly on the second level cycle , Because for each i We all have to go to the front to find an optimal prefix sequence , However, this problem cannot record a maximum value like the longest common subsequence below , Because here, the value of the back side may be smaller than that of the front side . So we use greedy thoughts , For the same length LIS We definitely hope that the smaller the ending, the better . At the same time, the sequence maintained in this way is monotonic , Therefore, we can use dichotomy to optimize, and finally make the time complexity of the algorithm ： $O (n l o n g n)$

f[i] Is defined as ： The length is i Of LIS The smallest value at the end of the element . Then our answer is i Value .
Why is it right ？ For one LIS When the sequence traverses to the back, if we update the end value , From the greedy thought, this is the best , It is also possible , For if we use the last value to modify a value in the middle , On the surface, we can't do this because we have to take it in order , But this will not affect the final result , Because it will not increase LIS The length of . say concretely , The value we want to modify is only the end value , However, its minimization , However, if you add a special judgment, it will be troublesome to only modify the end value , And any modification will not affect the final result , Then why not do it ？ Therefore, we can find the correct LIS The length of , But the value stored inside is not necessarily correct LIS Sequence . namely
however ！！！B[ ] The sequence in is not necessarily the correct longest ascending subsequence
We're looking for a better score than a[i] The first position greater than or equal to , So we can use lower_bound( ) function ： To achieve .// Returns the first greater than or equal to val Value position

Core code ：

#include <stdio.h>
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const  int N  = 1010, INF = 0x3f3f3f3f;
int n, cnt, a[N];
int f[N];
int find(int num) {
    
	//  Because of plus 1 after , Then subtract  f Then it's equivalent to f With 1 Start saving subscripts 
	return lower_bound(f + 1, f + 1 + cnt, num) - f;
}

int main() {
    
	cin >> n;
	for (int i = 1 ; i <= n ; ++i)
		cin >> a[i], f[i] = INF;
	f[1] = a[1], cnt = 1;
	// From 2 The number begins 
	for (int i = 2 ; i <= n ; ++i) {
    
		if (a[i] > f[cnt]) //  If it is larger than, it will be directly followed 
			f[++cnt] = a[i];
		else
			f[find(a[i])] = a[i];
	}

	cout << cnt << endl;

	return 0;
}

The above method is a little traversal dp 了 , So we're right dp Analyze the formula ：
Let's review O(n^2)DP State transfer equation of ：F [ i ] = max { F [ j ] + 1 ,F [ i ] } (1 <= j < i,A[ j ] < A[ i ])
We are recursing F When you have an array , Every time you put F Scan the array to find F[ j ] The maximum of , It's time consuming . We can optimize this process with the help of data structure . So how do we optimize ？ Our time-consuming is to maximize the previous conditions one by one , So can we do it faster ？ We can use tree array to maintain , Adopt the idea of building trees with numerical ranges , take LIS Record the maximum length . Then the process of taking the maximum value is optimized , However, when we use the tree array to maintain, we take a maximum value with all the items in front of the number , Therefore, for this number, we must ensure that its value must be large （ rising ）, So we can use structure to store values and numbers , Sort values , Then traverse from front to back , Then we must satisfy the ascending property when traversing .
Code ：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstdlib>
#include <cstring>
#include <cmath>
using namespace std;
const int maxn =103,INF=0x7f7f7f7f;
struct Node{
    
    int val,num;
}z[maxn]; 
int T[maxn];
int n;
bool cmp(Node a,Node b)
{
    
    return a.val==b.val?a.num<b.num:a.val<b.val;
}
void modify(int x,int y)// hold val[x] Replace with val[x] and y The larger number in  
{
    
    for(;x<=n;x+=x&(-x)) T[x]=max(T[x],y);
}
int query(int x)// return val[1]~val[x] Maximum of  
{
    
    int res=-INF;
    for(;x;x-=x&(-x)) res=max(res,T[x]);
    return res;
}
int main()
{
    
    int ans=0;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
    
        scanf("%d",&z[i].val);
        // If the title data does not say different , Need to be heavy .
        // If you don't remove the weight, it is to find the length of the longest non strictly monotonic ascending subsequence 
        z[i].num=i;// remember val[i] The number of , It is similar to discretization , But no weight loss  
    }
    sort(z+1,z+n+1,cmp);// Take the weight as the first keyword, sort from small to large  
    for(int i=1;i<=n;i++)// Enumerate from small to large by weight  
    {
    
        int maxx=query(z[i].num);// The query number is less than or equal to num[i] Of LIS Maximum length 
      
        modify(z[i].num,++maxx);// Put the length +1, Update the previous LIS length 
        ans=max(ans,maxx);// Update answers 
    }
    printf("%d\n",ans);
    return 0;
}

The longest non strictly increasing subsequence

This is almost the same as the above , Because it is not strict, it can be equal to , So we may just be equal to
Core code ：

for(int i = 2 ; i <= n ;++i){
    
	for(int j =  1 ; j < i ; ++j )
		if(a[i] >= a[j]) f[i] = max(f[i] , f[j] + 1);
}

For the second method ：

for (int i = 2 ; i <= n ; ++i) {
    
		if (a[i] >= f[cnt]) //  If it is larger than, it will be directly followed 
			f[++cnt] = a[i];
		else
			f[find(a[i])] = a[i];
	}

At least how many times can you change the sequence into an ascending sequence

about Non strictly increasing sequence , We only need to subtract the length of the longest non strictly increasing sequence from the total length of the sequence . Because for the number that is not in the longest non strictly increasing sequence, we can change it to be equal to the adjacent number .
For using Strictly increasing sequence , We first construct an array b, b[i] = a[i] - 1 , Then seek b The length of the longest non strictly increasing subsequence of the array , Then subtract the total length of the sequence to get the correct answer . as a result of ： For strictly increasing sequences, we have $a [i] > a [j] (i > j)$ The equivalent deformation is $a [i] - i > = a [j] - j$ . For this form, we find that the equals sign appears , So we construct a new sequence according to the above method . Then use this new sequence to find .

The longest common ascending subsequence

Title Transfer door
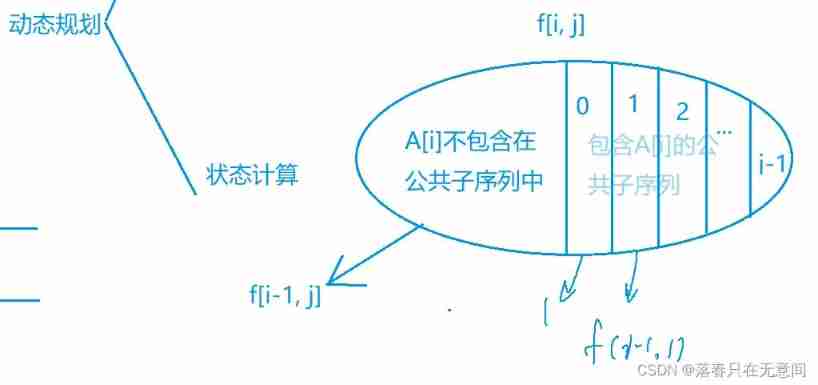
Insert picture description here

Now let's focus on , Part of state calculation .

First , According to the idea of the longest common subsequence , because b[j] It must be in this set, so let's see a[i] This element , There are two conditions for the title , One is public , This is the relationship between two sequences , One is rising, which is the relationship within the sequence . We will let the public , It is divided into a[i] Not in the common ascending subsequence a[i] There are two parts in the common ascending subsequence . For the previous part ,

That is to say f[i-1][j] The meaning of the , We all come from the meaning . For the latter part , We need the help of ,lat The concept , What does this mean , Just the last different place , Because the second half a[i] == b[j] Of , The difference is b[j] What is an element on . and b[j] The number of elements in front of the element may be 0~j-1 individual . about 0 The situation of , because b[j] There are no elements ahead , So as long as I satisfy the public, it must be rising, that is 1.（ Because I'm definitely on the rise ）. about 1 ~ j-1 . As long as their values are less than b[j] Then you can go max The calculation of , But in taking max When , Our formula is f[i][j] = max(f[i][j] , f[i-1][k] + 1); First of all, explain i - 1, And why we take with or without a[i] To distinguish between , This is related to our traversal , Our outer cycle is a , If our outer cycle is b, Then we can also take b[i] Whether to divide . And then there was f[i-1][k] + 1 . Because the premise here is a[i] = a[j] , Then the public conditions have been met , And then there is b[k] < b[j] , Then it meets the rising conditions, then ,f[i-1][k] It's the previous part of this ,1 yes a[i] == b[j] This part .
We have the following core code ：

for(int i = 1 ; i <= n ; ++i){
    
        for(int j = 1 ; j <= n ; ++j){
    
            f[i][j] = f[i-1][j];
            if(a[i] == b[j]){
    
                int maxv = 1;
                for(int k = 1 ; k < j ;  ++k)
                    if(b[k] < b[j])maxv = max(maxv , f[i-1][k] + 1);
                f[i][j] = max(maxv , f[i][j]);
            }
        }
    }
    int res = 0 ;
    for(int i = 1 ; i <= n ; ++i)res = max(res , f[n][i]);

The algorithm is $O(n^3)$ An order of magnitude , Let's try to optimize it .
because a[i] == b[j], The above code becomes ：if(b[k] < a[i])maxv = max(maxv , f[i-1][k] + 1);
Then the third layer of the cycle is ：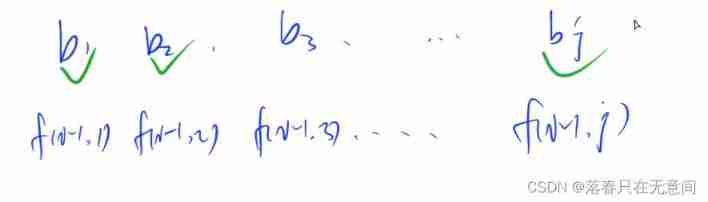
Insert picture description here
Here the side is smaller than a[i] Of , Because this is fixed , because b Which values are less than a[i] All have become settled . So this cycle is to find all b,b Satisfaction is less than a[i] Number of corresponding schemes +1 A maximum of .

for(int i = 1 ; i <= n ; ++i){
    
        int maxv = 1;
        for(int j = 1 ; j <= n ; ++j){
    
            f[i][j] = f[i-1][j];
            if(a[i] == b[j])f[i][j] = max(maxv  , f[i][j]);
            if(b[j] < a[i]) maxv = max(maxv,f[i-1][j] + 1 );
        }
    }

Grading problem

Questions are forwarded to you

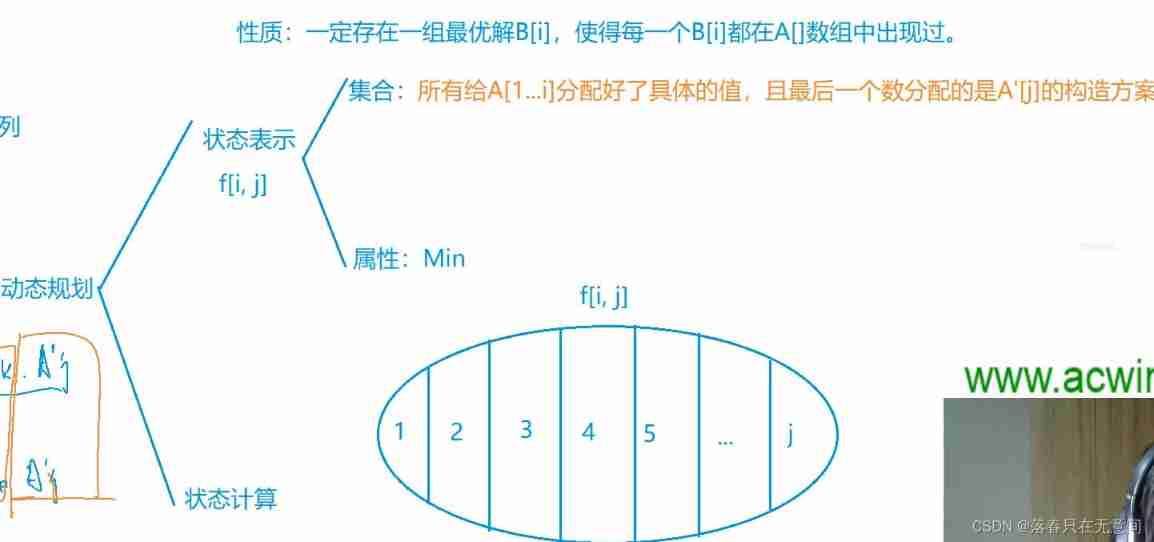
Insert picture description here

With the foreshadowing, let's talk directly about how to calculate the transition . First of all, for f[i][j] This state is fixed , It's my first i There must be b[j] This number is counted. , So in this case ( It means No i There must be b[j] All possible cases of this number ) , Or reference last The concept , Our first difference should be the value placed in the previous position , Due to the non strictly monotonic increasing property , The value we can put in the last position may be 1~j So we divide this problem . As for how to ask, let's see below

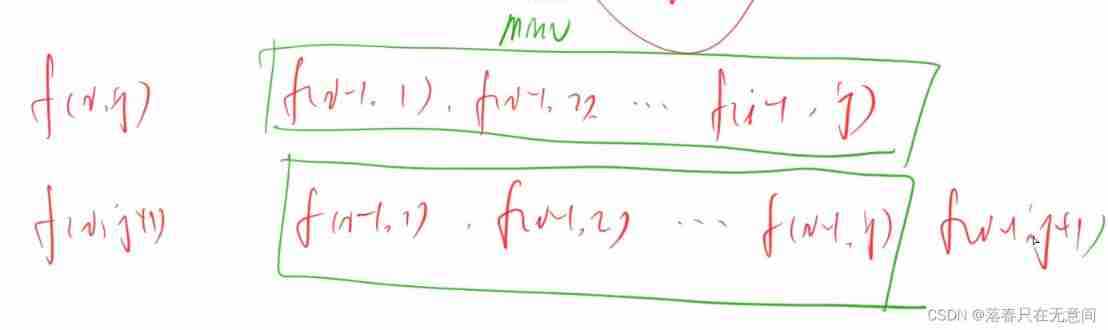
Insert picture description here

We found that if we use cycles to calculate , There will be a lot of double counting . We found that for the latter j In addition to f[i-1][j+1] Is with the j The time is different, and the rest are the same . So we can maintain this minimum value with a value .

Because there are two cases of non strict increasing and decreasing , Therefore, we can choose the minimum value in these two cases . So if we first find the increment , So just , Just flip the original array .

#include<stdio.h>
#include<iostream>
#include<algorithm>
#include<cmath>

using namespace std;

const int N = 2010 , INF = 0X3f3f3f3f3f;
int n , a[N] , b[N];
int f[N][N];

int dp(){
    
    for(int i = 1 ; i <= n ; ++i)b[i] = a[i];
    sort(b+1,b+1+n);
    for(int i = 1 ; i <= n ; ++i){
    
        int minv = INF;
        for(int j = 1 ; j <= n ; ++j){
    
            minv  = min(minv , f[i-1][j]);
            f[i][j] = minv + abs(b[j] - a[i]);
        }
    }
    int res = INF;
    for(int i = 1  ; i <= n ;++i)res = min(res , f[n][i]);
    return res;
}

int  main(){
    
    scanf("%d",&n);
    for(int i = 1 ; i <= n ; ++i)scanf("%d",&a[i]);
    int res = dp();
    reverse(a+1 , a+1+n );
    res = min(res , dp());
    printf("%d\n",res);
    return 0;
}

Mobile services

Topic transmission

Their thinking ：

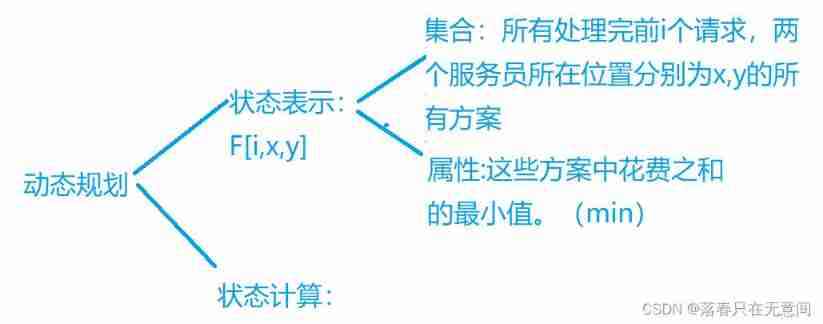
First of all, we need to think about how to express the state ？ We can use the number of requests completed as a stage , But this information alone is not enough , We need to add some information . In this subject , We use the positions of three waiters as additional information . So we have ,f[i][x][y][z] The meaning of the expression is to deal with i The positions of the three waiters after the request are x,y,z. Not enough. If we calculate directly like this, the time will be directly TM Of . Then we need to analyze whether these additional information is relevant ？ Starting from the meaning of the topic , When we deal with the i After a request, there must be a waiter in pos[i] In this position , Therefore, we only need two of the following three messages . Here we first draw a preliminary framework .

Then the next difficulty is the calculation of state . Dynamic programming is a special shortest path problem ( On a complementary graph ). Consider the calculation of states from the perspective of graph theory , In fact, that is , The transition relationship between different states （ There is a relationship with the edge ）

Transformation relations generally fall into two categories ：
Update the current state with the state it depends on .（80%）
Update the state that depends on it with the current state .
To draw a picture is
These two are actually equivalent .

Then we will take a look at this problem , In this state , For the current state f[i][x][y] There are only three states for it to go out , No more than is x The waiter goes , Or y Go to , Or z Go to . And its entry edge is very complicated . Therefore, we choose the second method to calculate this problem .

inspire ：

Find linearity DP The problem of , Usually first determine “ Stage ”. If “ Stage ” Not enough to represent a state , You need to take the required additional information as the dimension of the state .
In determining DP In the state of , Choose the smallest one that can cover the whole state space ： Dimension set . For example, we can certainly express this problem in four dimensions , But it's not better to express it in three dimensions .

Code ：

#include<stdio.h>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

const int N = 1010 , M = 210;
int n , m  , pos[N];
int w[M][M] , f[N][M][M];

int main(){
    
    scanf("%d%d",&m,&n);
    for(int i = 1 ; i <= m ; ++i)
        for(int j  = 1 ; j  <= m ; ++j)
            scanf("%d",&w[i][j]);
    for(int i = 1 ; i <= n  ;++i)scanf("%d",&pos[i]);
    memset(f , 0x3f , sizeof f);
    pos[0] = 3 , f[0][1][2] = 0;
    for(int i = 0 ; i < n ; ++i)
        for(int x = 1 ;  x <= m ; ++x)
            for(int y = 1 ; y <= m ; ++y){
    
                int z = pos[i] , u = pos[i+1] , val = f[i][x][y];
                if(x == y || x == z || y == z)continue;
                f[i+1][x][y] = min(f[i+1][x][y] , val + w[z][u]);
                f[i+1][z][y] = min(f[i+1][z][y] , val + w[x][u]);
                f[i+1][x][z] = min(f[i+1][x][z] , val +w[y][u]);
            }
    int res = 0x3f3f3f3f;
    for(int x = 1 ; x <= m ; ++x)
        for(int y = 1 ; y <= m ; ++y){
    
            int z = pos[n]; // Because requests are processed sequentially , Therefore, the final processing should be this request .
            if(x == y || y == z || x == z)continue;
            res  = min(res , f[n][x][y]);//
        }
        printf("%d\n",res);

    return 0;
}

Pass slip

Title Transfer door

Their thinking ：

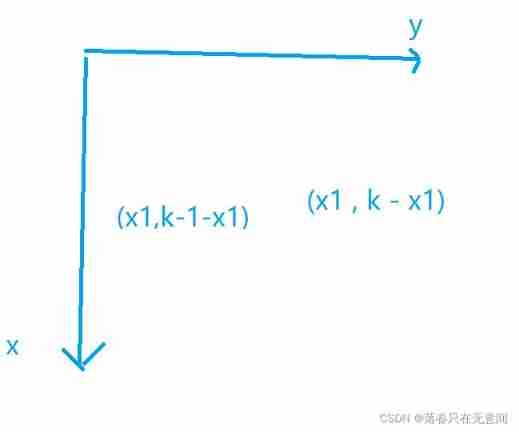
First of all, let's recall how we decide the state if we can only take one path ：f[i][j]: Said go $x_i,y_j)$ The maximum value of the sum of this path . Then we can define it similarly as ：f[x1][y1][x2[y2]. But inspired by the above, let's try to think about whether we can narrow the state space ？ We used two coordinates , It is to judge whether it is on the same grid, that is x1 == x2 && y1 == y2, But it's too detailed . If we record the sum of abscissa and ordinate , Then if it is the same as , Only x Same, then you can judge . So our final state is ：f[k]x1][x2];

So what, how to get the expression from the meaning of the divided sub interval ？

analogy , We get the expressions of the four intervals as ：

Two people go right at the same time , The maximum score is f[k - 1, i, j] + score(k, i, j);
The first person walks to the right , The second man walked down , The maximum score is f[k - 1, i, j - 1] + score(k, i, j);
The first person walks down , The second man walks to the right , The maximum score is f[k - 1, i - 1, j] + score(k, i, j);
Two people go down at the same time , The maximum score is f[k - 1, i - 1, j - 1] + score(k, i, j);

There is also a point of attention x The scope of the , We have $1 < = x < = n and 1 < = k - x < = m$ obtain
$m a x (1, k - m) < = x < = m i n (n, k - 1)$

For this problem, it can also be related to square counting , The relevant proof is this blog ： Blog

Code ：

#include<stdio.h>
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 55;
int n , m ;
int w[N][N],  f[N<<1][N][N];

int main(){
    
    cin>>n>>m;
    for(int i = 1 ; i <= n ; ++i)
        for(int j = 1 ; j <= m ; ++j)
            cin>>w[i][j];
    
    for(int k = 2 ; k <= n + m ; ++k)
        for(int x1 = max(1 , k - m) ; x1 <= min(n , k -1) ; ++x1)
            for(int x2 = max(1,k-m);  x2 <= min(n, k - 1) ; ++x2)
            {
    
                int t = w[x1][k-x1] ;
                if(x1!=x2) t += w[x2][k-x2];
                for(int a = 0 ; a <= 1 ; ++a)
                    for(int b= 0 ; b <= 1 ; ++b)
                        f[k][x1][x2] = max(f[k][x1][x2] , f[k-1][x1-a][x2-b] + t);
            }
    cout<<f[n+m][n][n]<<endl;
    
    return 0;
}

Ranking inequalities

Insert picture description here

knapsack problem

Preface

I believe everyone should have seen many blogs or videos about backpacking . However, the above framework is used here for analysis . I hope everyone can understand the above and have a deeper understanding of the above application . At the same time, I also made some clever arrangements in the order of backpacking .

01 knapsack problem

Topic transmission

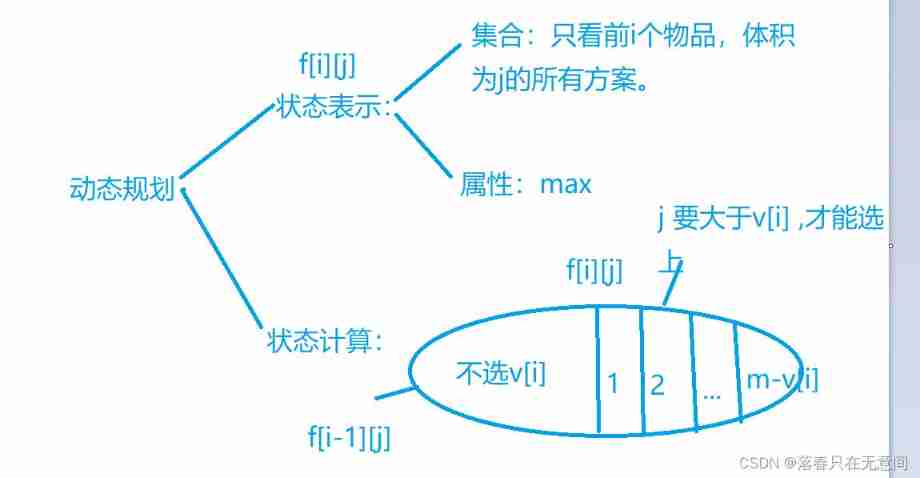
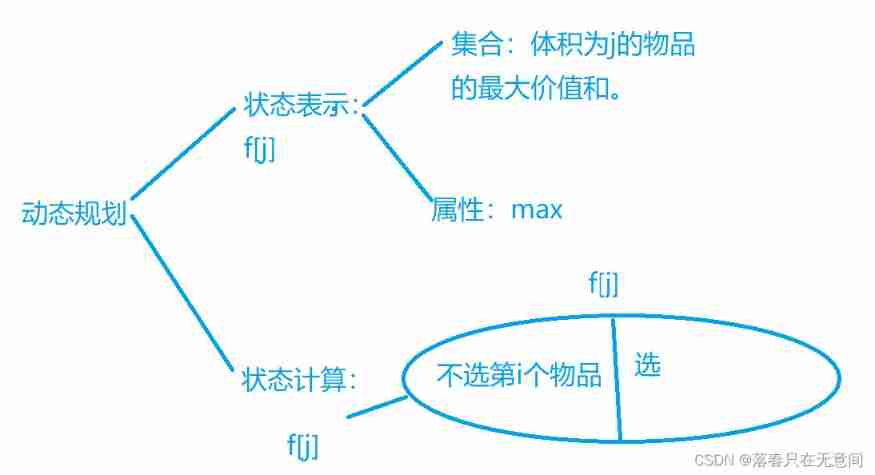
Here's the picture ： Let's mainly talk about state calculation . about f[i][j] Let's compare the last difference of all these schemes in this set , about i For some, it may be that they didn't take the first i The volume of an object is j 了 . Therefore, it is divided into two divisions: take and do not take . For this part , Then the last of them is taken i The items are the same , So their last The difference is that I didn't take the first i Of items j Different .
We are generally divided into two parts: change and invariance , These plans are finally taken V[I] The value is the same , Then the difference is the former i - 1 , Total volume of items . In order to get it, the total volume cannot be less than W[I[

Tips ：

For a decimal ： It can be used memset(f , 0xcf , sizeof f); To initialize the .

Code ：

#include<iostream>
#include<cstring>
using namespace std;
const int N = 1010;
int n , V;
int v[N] , w[N];
int f[N][N];
int main(){
    
    memset(f , 0xcf , sizeof f);
    cin>>n>>V;
    for(int i = 1 ; i <= n ; ++i)cin>>w[i]>>v[i] ;
    f[0][0] = 0;
    for(int i = 1 ; i <= n ; ++i)
        for(int j = 0 ; j <= V ; ++j){
    
            f[i][j] = f[i-1][j];
            if(j >= w[i])
                f[i][j] = max(f[i][j] , f[i-1][j-w[i]] + v[i]);
        }
    int res = 0;
    for(int i = 1 ; i <= V ; i++) res = max(res , f[n][i]);
    cout<<res<<endl;
    return  0;
}

We observed that , Every time I ask for i Only with i-1 Stratification , So we don't have to record all the States , And use Scrolling array To optimize . Here is another optimization , We found that , At the beginning of each stage , Actually f[i-1][] To f[i][] A copy of the , Then can we optimize the state space into one dimension ？f[j] Indicates that the total volume of the backpack is j The maximum value of your goods .
First write a preliminary equivalent change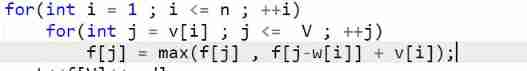
Insert picture description here

However, in the second layer of circulation, we should pay attention to , Before, we were f[i-1][j-w[i]] + v[i] We are looking for the first i In the second stage, we use the i-1 Stage information . Now if there is V = 2 * w[i] Words , Then there is f[V] = max(f[V] , f[w[i]] + v[i]) , and f[w[i]] We just figured it out at this stage, which is obviously inconsistent . And the solution to this is also very simple , We just need , Just traverse in reverse order .

Tips ： If we make f Arrays are all 0, Not just f[0] = 0 , So the end result is f[V]
Code ：

#include<stdio.h>
#include<iostream>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110, M = 1e5 + 10;
typedef long long LL;
int n, W;
int w[N], v[N] ;
LL f[M];

int main() {
    
	cin >> n >> W;
	for (int i = 1; i <= n ; ++i)
		cin >> w[i] >> v[i];
	for (int i = 1; i <= n ; ++i)
		for (int j = W ; j >= w[i]; --j)
			f[j] = max(f[j], f[j - w[i]] + v[i]);
	LL res = 0 ;
	for (int i = 1 ; i <= W ; ++i)
		res = max(res, f[i]);
	cout << res << endl;

	return 0;
}

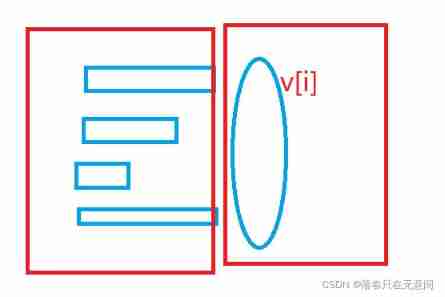
01 Backpack advanced

Ordered above 01 The time complexity of backpacking is O（NM） among N Is the number of items ,M It's the volume of the backpack . So if the problem is that the backpack is very large , But when the value of each item is relatively small, it can't be used .
The expression of our transition above is dp[j]: The volume is j The maximum value of your goods . Then we can change the meaning into ：dp[i]： The value is i The minimum volume of the article .
Then we can solve this kind of situation .

Code ：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1E5 + 10;
typedef long long LL;
int n, m ;
LL f[N] ;
int w[110], v[110];

int main() {
    
	memset(f, 0x3f, sizeof f );
	int sum = 0, res = 0;
	cin >> n >> m;
	for (int i = 1 ; i <= n ; ++i) {
    
		cin >> w[i] >> v[i];
		sum += v[i];
	}
	f[0]  = 0;
	for (int i = 1; i <= n ; ++i)
		for (int j = sum ; j >= v[i] ; --j) {
    
			f[j] = min(f[j], f[j - v[i]] + w[i]);
			if (f[j] <= m)
				res = max(j, res);
		}
	cout << res << endl;
	return 0;
}

Number combination

Topic transmission

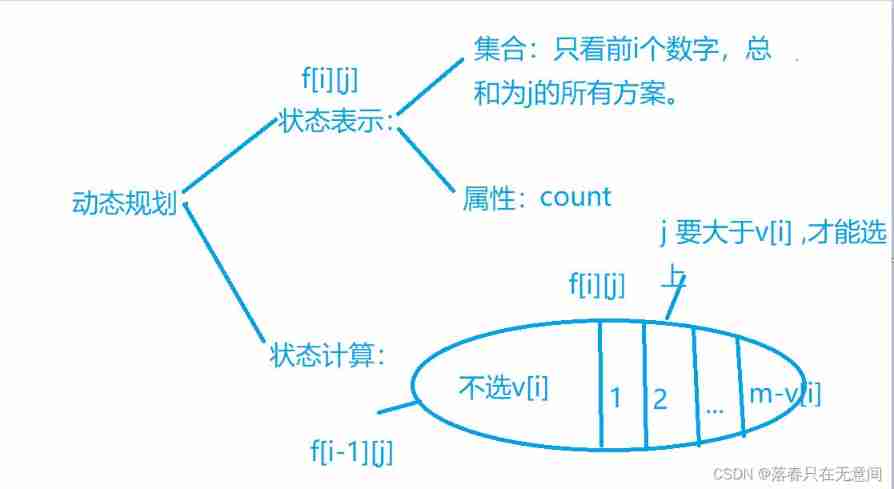
The reason for putting these two together , Because they are essentially the same, but the attributes have changed .
Let's start by writing some dynamic programming frameworks

Right, amazing acquaintance . However, the number of schemes is calculated here . So let's talk about the part of state calculation . First, the left half , Then we can directly add the number of schemes it means . But for each stage f[i][j] Values are 0, So we can write as f[i][j] = f[i-1][j]; For the right part , We just have to take max Change the operation to add . Using the tips mentioned above, we directly output f[n][m] That's the answer .

Code ：

#include<stdio.h>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;

const int N = 110 , M = 1e4 + 10;
int n , m ;
int a[N] , f[N][M];

int main(){
                 
    cin>>n>>m;
    for(int i = 1 ; i <= n ;++i) cin>>a[i] ;
   f[0][0] = 1;
    for(int i = 1 ; i <= n ; ++i){
    
        for(int j = 0 ; j <= m ; ++j)
         {
       
             f[i][j] = f[i-1][j];
             if(j >= a[i])
            f[i][j] += f[i-1][j-a[i]];
         }
    }
   cout<<f[n][m]<<endl;
    return 0;
}

Or consider the optimized version ：

#include<stdio.h>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;

const int N = 110 , M = 1e4 + 10;
int n , m ;
int a[N] , f[M];

int main(){
                 
    cin>>n>>m;
    for(int i = 1 ; i <= n ;++i) cin>>a[i] ;
   f[0] = 1;
   for(int i = 1 ; i <= n ; ++i)
    for(int j = m ; j >= a[i] ; --j)
        f[j] += f[j-a[i]];
    cout<<f[m]<<endl;
    return 0;
}

Completely backpack

Title Transfer door

Complete backpack with 01 The difference between backpacks is that each item can be selected infinitely , As long as the volume does not exceed the upper limit .

If we directly use the above 01 If the knapsack is traversed in reverse order , We can just write like this .( The first i You can choose multiple items ) But the time complexity is $O(n^2 long(n))$ You can't .

Talk about optimization 01 When I was backpacking , We are 1 In the calculation of i Only use i-1 Three stages , So we enumerate from big to small . For complete knapsack, we only need to change the reverse order into positive order .

#include<iostream>
using namespace std;
const int N = 1010;
int n , m, w[N] , v[N];
int f[N];

int main(){
    
    cin>>n>>m;
    for(int i = 1 ; i <= n ; ++i)cin>>w[i]>>v[i];
    for(int i = 1 ; i <= n ; ++i)
        for(int j = w[i] ; j <= m ; ++j  )
            f[j] = max(f[j] , f[j-w[i]] + v[i]);
    cout<<f[m]<<endl;
    return 0;    
}

Natural number splitting

Topic transmission

Their thinking ：

We will use natural numbers N It is regarded as having a capacity of N A backpack , Then this question is 1 ~N altogether N Items , The volume of each article ranges from 1 ~N , Ask if these numbers are combined into N The number of all programs , But because it can be reused , So the problem is a complete knapsack model .

At the same time, this topic will explode int Of , So we use unsigned ： $2^{32} - 1$ .
stay c++ One of the properties in is the result of a negative number on the module and the absolute value of the negative number on the module （ Positive numbers ） It's the same thing .

jury

Topic transmission

Their thinking ： What we are looking for is the least difference , Because the difference between the two topics is $- 400 - - - 400$ Then we have a train of thought that is to divide by difference , After calculation , The median difference is 0 Start looking on both sides in turn , The first one I found ( Because of symmetry, one positive and one negative ) It's the one with the smallest difference , Compare the two to find the maximum , Let's sort out our ideas through the framework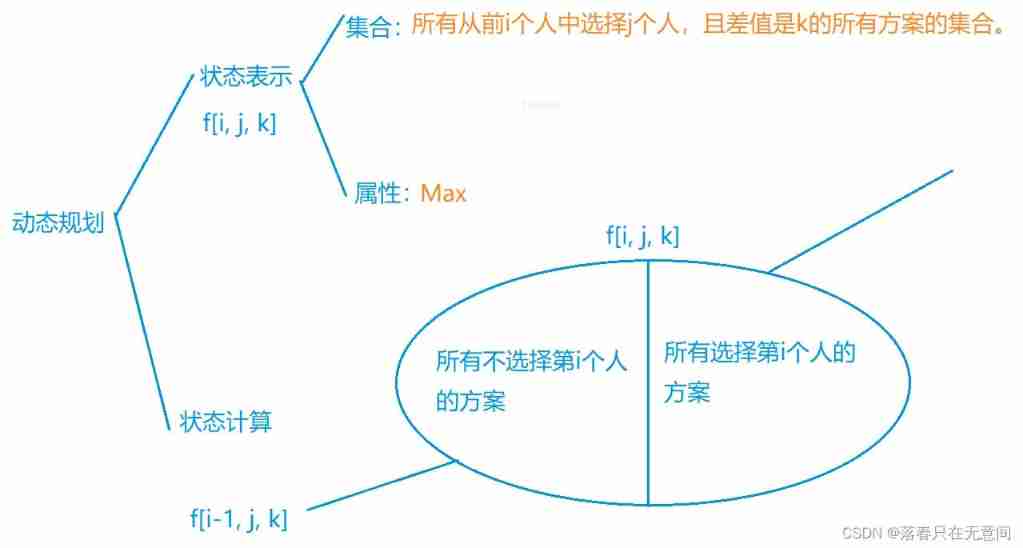
Insert picture description here

Let's focus on the state calculation . Combined with the idea of knapsack problem , about f[i][j][k] We find out the final differences to divide the set . First , For the first i There are two kinds of personal choices . If you don't choose from the meaning, it means f[i-1][j][k], If you choose ,

We will take the second part , All situations of are divided into two parts: change and invariance , For the constant is the first i personal , So the meaning of the previous part is ： front i-1 In the personal , Yes j-1 personal , The difference is k - (p[i] - d[i]) And this is just f[i-1][j-1][k - (p[i]-d[i])].

Difficulties in implementation ： Because the array subscript cannot be negative , So we set an offset , about 0~399 A negative number ,401~800 It means a positive number .
Where you can prune , Because we know the difference can only be in -400~400 Between , That is, after the offset 0~800. Therefore, if it is not within this range, it is definitely not the answer . Another is that we are before the second plan j It has to be greater than 1 Can only be .
Another difficulty is that this problem also needs to output a correct program sequence ： Generally, there are two solutions , One is to open another array to store the state of the transition process , The other is to deduce the scheme backwards , Here we use the backward solution . For this method , When we push backward, we see that one of the most important values of the current value is dp Where do you get it in the formula , Another key point is , Understand the changes between variables when extrapolating .

Code ：

#include<stdio.h>
#include<algorithm>
#include<iostream>
#include<cstring>
using namespace std;

const int N = 210,M = 810 , base = 400;
int n , m ;
int ans[N] , p[N] , d[N];
int f[N][21][M];
int main(){
    
    int T = 1;
    while(scanf("%d%d",&n,&m),n&&m){
    
        for(int i = 1 ; i <= n;  ++i)scanf("%d%d",&p[i],&d[i]);
        memset(f , -0x3f , sizeof f);
        f[0][0][base] = 0 ;
        for(int i = 1 ; i <= n ; ++i)
            for(int j = 0 ; j <= m; ++j )
                for(int k = 0 ; k < M ; ++k){
    
                    f[i][j][k] = f[i-1][j][k];
                    int t = k - (p[i] - d[i]);
                    if(t <0 || t >= M)continue;
                    if(j < 1)continue;
                    f[i][j][k] = max(f[i][j][k] , f[i-1][j-1][t] + p[i] + d[i]);
                }
        int v = 0 ;
        while(f[n][m][base - v] < 0 && f[n][m][base+v] < 0)v++;
        
        if(f[n][m][base-v] > f[n][m][base+v]) v = base - v;
        else v = base + v;
        int cnt = 0 , i = n , j = m , k = v;

        while (j)
        {
    
            if (f[i][j][k] == f[i - 1][j][k]) i -- ;
            else
            {
    
                ans[cnt ++ ] = i;
                k -= (p[i] - d[i]);
                i --, j -- ;
            }
        }
        int sp = 0 , sd = 0;
        for(int i = 0 ; i < cnt ; ++i) sp += p[ans[i]] , sd += d[ans[i]];
        
        printf("Jury #%d\n",T++);
        printf("Best jury has value %d for prosecution and value %d for defence:\n",sp,sd);
        sort(ans, ans + cnt);
        for(int i = 0 ; i < cnt ; ++i)printf(" %d",ans[i]);
        puts("\n");
    }
    return 0;
}

Let's explain the backward process in the code , First of all, we make it clear that we are going to choose m The personal number is output , So the initial condition of our cycle condition is m personal , Only did not arrive 0 That is, it hasn't been recorded yet . Let's see dp The formula in , One is possible from f[i-1][j][k] Transferred from this state , If so , So the previous state corresponds to i - 1 , So we have to i – . Otherwise, it is by f[i-1][j-1][k-(p[i] - d[i])] obtain , Because we need to let k-(p[i] - d[i]), then i-- , j--;

Multiple backpack

Topic transmission

For multiple backpacks , Let's first think that the simplest way is to turn it into 01 Knapsack problem to solve . It's transforming into 01 We have two ideas about backpacking ：

The original 01 The backpack frame should be this , One idea is to choose this step to improve . about 01 We only need to choose backpacks or not , For multiple backpacks, we may choose 1… c[i] individual . Then there is

So there is ：

#include<iostream>
using namespace std;
const int N = 110;
int f[N] , n , m;

int main(){
    
    cin>>n>>m;
    for(int i = 1 ; i <= n ; ++i){
    
        int w , v , s;
        cin>>w>>v>>s;
        for(int j = m ; j >= w ;  --j)
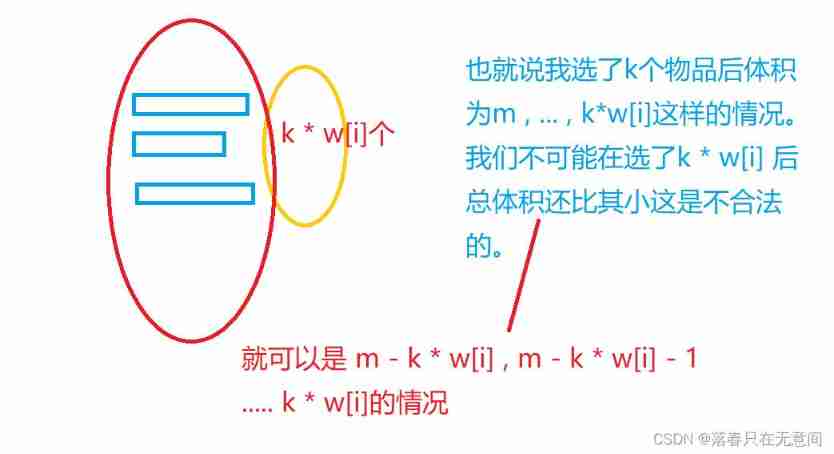
         // k * w <= j ,  That is, the previous state after I selected these cannot be less than 0 Of 
            for(int k = 1 ; k <= s && k * w <= j ; k++)
                f[j] = max(f[j] , f[j- k * w] + k * v); 
    }
    cout<<f[m]<<endl;
    return 0;
}

Another idea is that I will k * w[i[, It is divided into k Time 01 knapsack , That is to say, it is divided into one by one , And then use it 01 Knapsack writing solution . These two approaches are equivalent .

Code ：

#include<iostream>
using namespace std;
const int N = 110;
int f[N] , n , m;

int main(){
    
    cin>>n>>m;
    for(int i = 1 ; i <= n ; ++i){
    
        int w , v , s;
        cin>>w>>v>>s;
        for(int k = 1 ; k <= s ; ++k)
            for(int j = m ; j >= w ;  --j)
                f[j] = max(f[j] , f[j-  w] +  v); 
    }
    cout<<f[m]<<endl;
    return 0;
}

Binary optimized version

First, let's recall that the above is directly split into 01 The problem with backpacks , We split them into items one by one , So our complexity is very high . Here we want to clarify a problem ？ about 0~n Number of numbers , How many numbers do we need to use to express them , Of course you can , When the most stupid way is n individual 1 , If you choose none, it means 0, choose n individual 1 It means n. However, it is obvious that the above split method is not desirable . Here we have a conclusion ： Need at least $log_{2}{n}$ Such a number . How can this be achieved ？ like 10： 1 2 4 8 . This is obviously not possible , Because that means 0~15 Greater than 10 了 . So we are not more than $2^k$ If so, just use the rest , Namely ：1 , 2 ,4,3. That's it .

Code ：

#include<stdio.h>
#include<iostream>
#include<vector>
using namespace std;
const  int N = 2010;
int n , m ,f[N];

struct GOOD{
    
    int v,w;
};

int main(){
    
    cin>>n>>m;
    vector<GOOD>goods;
    for(int i = 1 ; i <= n ; ++i){
    
        int v ,w, s;
        cin>>w>>v>>s;
        for(int k = 1 ; k <= s ; k *=2){
    
            s -= k;
            goods.push_back({
    k*v,  k *w});
        }
        if(s >  0) goods.push_back({
    s*v,s*w});
    }
    
    for(auto good : goods){
    
        for(int j = m ; j >= good.w ; --j)
            f[j] = max(f[j] , f[j - good.w] + good.v);
    }
    
    cout<<f[m]<<endl;
    
    return 0;
}

Monotonic queue optimization

Transfer door

Pack in groups

Topic transmission
Their thinking

This question can be said to be 01 Expand the backpack model , And 01 Backpacks are a little different , When selecting a stack of items, we need to enumerate all the items in this push and select only one . Me 01 The question is whether to choose this push item , If you choose, you can only choose one of these tweets . You can also think from another angle , Multiple knapsack is a special case of this kind of problem , For multiple backpacks, we can regard an item and its quantity as a pile of items . In this pile of items , Respectively 1 This item ,…,s This item .

Code ：

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 110;
int n , m ;
int w[N] , v[N] ;
int f[N];

int main(){
    
    cin>>n>>m;
    for(int i = 1 ; i <=n ; ++i){
     //  Which group 
        int s;
        cin>>s;
        for(int i = 1 ; i <= s ; ++i)cin>>w[i]>>v[i];
        for(int j = m ; j >= 1 ; j--) //  Volume 
            for(int k = 1 ; k <= s; k++) //  Which item to choose 
                if(j >= w[k])f[j] = max(f[j] , f[j-w[k]] + v[k]);
    }
    cout<<f[m]<<endl;
    return 0;
}

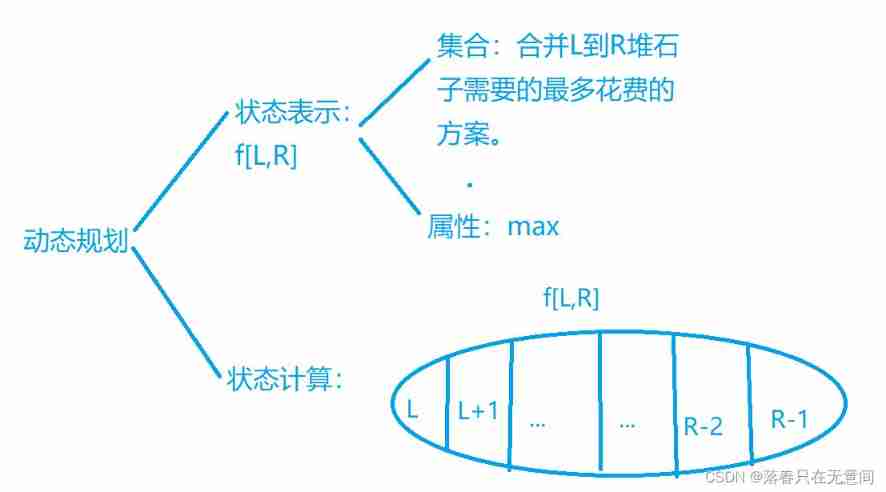
Section DP

In the interval DP in , A state is transferred by several states smaller than it and represented by its intervals . Section DP Generally, it is the length of enumeration interval , Left end point , And the location of the partition .（ Because the right endpoint can be obtained from the interval length and the left endpoint ）.

Ring stones and

Their thinking ： The key point of this question is , You can only merge adjacent stones , So we can know if we can merge in l and r Two stone piles in the location , It shows that the stone pile in the middle has been merged completely . Here is the analysis process ：( We show by analyzing the maximum cost ）

Let's explain the state calculation , For this problem, we can't calculate directly , Then we will divide it into sub problems , Divide and rule is simple . For all sums L and R All of our plans , Let's think about their final differences , The difference should be in which position in the middle k As a dividing point, it will [L,R] The interval is divided into [L,K], and [K+1,R] Two parts , So what we have to do is enumerate k The location of . At the same time, we are merging an interval [L,R] You need to start from L To R A price of the sum of numbers , In this step, we can use prefix to optimize .

For the ring, we usually split it into 2n A chain of . Only our left and right endpoints will change , Then we traverse one side [fi,n+i-1]（ It means on the i Disconnect the ring at ） Take a maximum .

Code ：

int n;
int a[MAXN];
int g[MAXN][MAXN],f[MAXN][MAXN];  // Maximum and minimum 
int sum[MAXN];
 
int main(){
    
	scanf("%d",&n);
	for(int i =1;i<=n;i++){
    
		scanf("%d",&a[i]);
		a[n+i] = a[i];  // structure 
	}
	
	for(int i=1;i<=2*n;i++){
      // The prefix and 
		sum[i] =sum[i-1] + a[i];
	}
	
	memset(g,0x3f,sizeof(g));
	memset(f,-0x3f,sizeof(f));
	
	for(int lena=1;lena<=n;lena++){
    
		for(int l=1;l+lena-1 <=n*2;l++){
    
			int r = l + lena -1;
			if(l == r){
    
				g[l][r] = f[l][r] = 0;
			}
			else {
    
				for(int k = l;k < r;k++){
    
				g[l][r] = min(g[l][r],g[l][k]+g[k+1][r] + (sum[r] - sum[l-1]));
				f[l][r] = max(f[l][r],f[l][k]+f[k+1][r] + (sum[r] - sum[l-1]));
			}
			}
			
		}
	}
	int maxn = -INF,minx = INF;
	for(int i=1;i<=n;i++){
       // see n Which kind of partition is the largest and smallest 
		minx = min(minx,g[i][i+n-1]);
		maxn = max(maxn,f[i][i+n-1]);
	}
	printf("%d\n%d\n",minx,maxn);
	return 0;
}