AtCoder Grand Contest 013 E - Placing Squares

Portal ：E - Placing Squares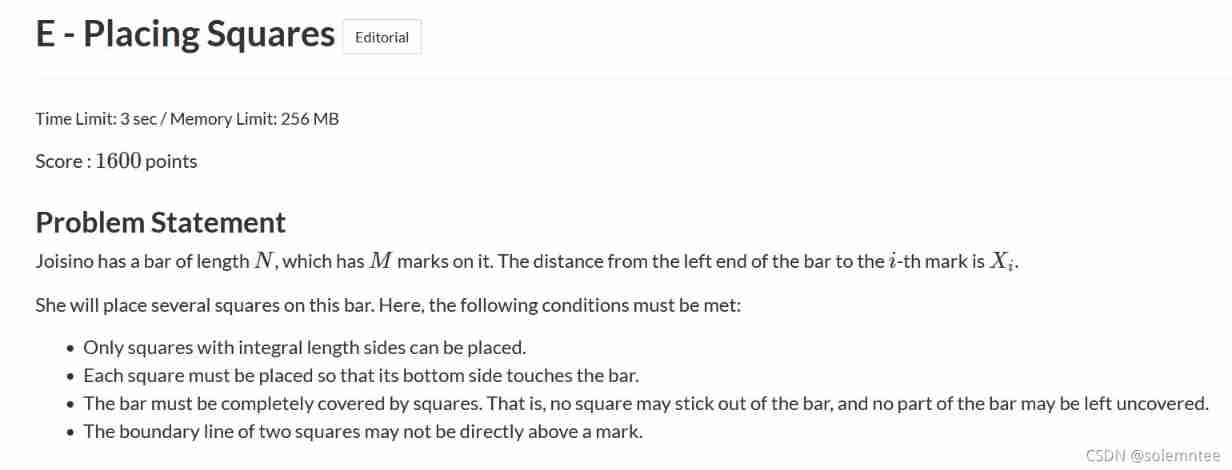
The question ： Now there is one with a length of n The stick
On the stick $m$ A sign , The first i The distance between the marks and the left endpoint is $x_i$
You need to put some squares on this stick , Satisfy ：

 The side length of each square is a positive integer 
 Each square must have a side close to the stick 
 The stick must be completely covered , The boundary of the square cannot exceed the stick 
 The junction of two adjacent squares cannot be marked 

Define the beauty degree of each scheme as the product of all square areas
Seek the sum of the beauty of all legal schemes , The answer is right $10^9+7$ modulus

First of all, let's enjoy the official explanation

First of all, the contribution and can be transformed into the number of schemes through a clever transformation . Modify the model of the original problem slightly ： Now there is $n$ Consecutive spaces , Partition plates must be placed on the left and right boundaries , You can place partitions in two adjacent spaces , You can put red and blue balls in the space . Contribution and the number of solutions equivalent to the converted problem , This becomes a count $dp$.
consider $dp[i][j]$ Before considering $i$ position , After the last partition $j$ The number of ball schemes .
Consider the transfer of violence enumerated in section $i$ There's a place for $(0,1,2)$ Ball and whether it is in the $i$ Place the baffle in two places , The specific derivation process will not be repeated
$$\begin{gathered} dp[i][0]=dp[i-1][0]\ast 2+dp[i-1][1]\ast 2+dp[i-1][2]\ast 1 \\ dp[i][1]=dp[i-1][0]\ast 1+dp[i-1][1]\ast 1+dp[i-1][2]\ast 0 \\ dp[i][0]=dp[i-1][0]\ast 1+dp[i-1][1]\ast 2+dp[i-1][2]\ast 1... \end{gathered}$$
amount to
$$ANS[i]=\left\{\begin{array}{ccc}2& 2& 1\\ 1& 1& 0\\ 1& 2& 1\end{array}\right\}\ast ANS[i-1]$$
Obviously, the matrix can be used for fast power optimization .
Of course, the transfer at the diaphragm is slightly different , No more details here .

#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7;
const int N=3;
struct Matrix{
    
    int a[N][N];
    Matrix(){
    memset(a,0,sizeof(a));}
    Matrix operator *(const Matrix &B)
    {
    
        Matrix c;
        for(int k=0;k<N;k++)
        for(int i=0;i<N;i++)
        for(int j=0;j<N;j++)
        c.a[i][j]=(c.a[i][j]+1LL*a[i][k]*B.a[k][j]%mod+mod)%mod;
        return c;
    }
}A,B,C,D;

Matrix fpow(Matrix A,long long b)///A^b
{
    
    Matrix ret,B=A;
    for(int i=0;i<N;i++)ret.a[i][i]=1;
    while(b)
    {
    
        if(b&1)ret=ret*B;
        B=B*B;
        b>>=1;
    }
    return ret;
}
void init()
{
    
    A.a[0][0]=2,A.a[0][1]=2,A.a[0][2]=1;
    A.a[1][0]=1,A.a[1][1]=1,A.a[1][2]=0;
    A.a[2][0]=1,A.a[2][1]=2,A.a[2][2]=1;

    B.a[0][0]=1,B.a[0][1]=0,B.a[0][2]=0;
    B.a[1][0]=1,B.a[1][1]=1,B.a[1][2]=0;
    B.a[2][0]=1,B.a[2][1]=2,B.a[2][2]=1;

    C.a[0][0]=1,C.a[0][1]=2,C.a[0][2]=1;
    C.a[1][0]=0,C.a[1][1]=0,C.a[1][2]=0;
    C.a[2][0]=0,C.a[2][1]=0,C.a[2][2]=0;
}
int a[1000005];
int main()
{
    
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)scanf("%d",&a[i]);
    init();
    Matrix ans;
    ans.a[0][0]=1;

    for(int i=1;i<=m;i++)
    {
    
        ans=fpow(A,a[i]-a[i-1]-1)*ans;
        ans=B*ans;
    }
    ans=fpow(A,n-a[m]-1)*ans;
    ans=C*ans;
// for(int i=0;i<N;i++)
// {
    
// for(int j=0;j<N;j++)
// {
    
// printf("%d%c",ans.a[i][j],(j==N-1)?'\n':' ');
// }
// }
    printf("%d\n",(ans.a[0][0]%mod+mod)%mod);
    return 0;
}