当前位置:网站首页>2017 USP Try-outs C. Coprimes
2017 USP Try-outs C. Coprimes
2022-07-05 05:31:00 【solemntee】
Portal :Coprimes
 The question : Give you a length of n n n Array of , ask l l l To r r r Whether there are mutual prime pairs between positions ( a [ i ] , a [ j ] ) = 1 ( i ≠ j ) (a[i],a[j])=1(i\not=j) (a[i],a[j])=1(i=j)
The question : Give you a length of n n n Array of , ask l l l To r r r Whether there are mutual prime pairs between positions ( a [ i ] , a [ j ] ) = 1 ( i ≠ j ) (a[i],a[j])=1(i\not=j) (a[i],a[j])=1(i=j)
For each location l l l, We can find the smallest r r r, bring [ l , r ] [l,r] [l,r] There are coprime pairs between .
With l l l The increase of , r r r It must increase , So we can consider taking a ruler . When the right endpoint enters and the left endpoint exits , We try to maintain the number of non coprime pairs in the interval p a i r pair pair.
about μ ( x ) ≠ 0 μ(x)≠0 μ(x)=0 Of x x x, We use it c n t [ x ] cnt[x] cnt[x] maintain , Among the factors of how many numbers are in the interval x x x, then , Did not enter a right endpoint r r r when , Then each d ∣ a [ r ] d|a[r] d∣a[r] And μ ( d ) ≠ 0 μ(d)≠0 μ(d)=0 And d ≠ 1 d≠1 d=1 Of d d d Yes p a i r pair pair The contribution of − μ ( d ) c n t [ d ] −μ(d)cnt[d] −μ(d)cnt[d], Add this contribution to p a i r pair pair In go to , Empathy , Exit one endpoint after another , Take this contribution from p a i r pair pair Subtract from .
In short , Build a bucket , c n t [ x ] cnt[x] cnt[x] To maintain x x x Number of multiples , Then in the set and a [ x ] a[x] a[x] The number of non reciprocal primes is equal to
∑ d ∣ a [ i ] , d ≠ 1 − μ ( d ) c n t [ d ] \sum_{d|a[i],d\not=1} -μ(d)cnt[d] d∣a[i],d=1∑−μ(d)cnt[d]
because 1 It cannot be used as a common factor, so it can be excluded c n t [ 1 ] cnt[1] cnt[1] It makes no sense , We skip 1, All the following numbers should be reversed
#include<bits/stdc++.h>
using namespace std;
int nxt[500005];
bool vis[10000005];
int pri[1000005];
int mo[1000005];
int tot=0;
void init(int n)
{
memset(vis,0,sizeof(vis));
mo[1]=1;
for(int i=2;i<=n;i++)
{
if(!vis[i])pri[++tot]=i,mo[i]=-1;
for(int j=1;j<=tot&&pri[j]*i<=n;j++)
{
vis[i*pri[j]]=1;
if(i%pri[j]==0)
{
mo[i*pri[j]]=0;
break;
}
else mo[i*pri[j]]=mo[i]*-1;
}
}
}
int nowans=0;
int CNT[500005];
int a[500005];
void addcnt(int id,int w)
{
for(int i=1;i*i<=a[id];i++)
{
if(a[id]%i==0)
{
if(i*i==a[id])CNT[i]+=w;
else
{
CNT[i]+=w;
CNT[a[id]/i]+=w;
}
}
}
}
void add(int id,int w)
{
for(int i=1;i*i<=a[id];i++)
{
if(a[id]%i==0)
{
if(i*i==a[id])
{
nowans+=mo[i]*w*CNT[i];
}
else
{
nowans+=mo[i]*w*CNT[i];
nowans+=mo[a[id]/i]*w*CNT[a[id]/i];
}
}
}
}
int main()
{
init(500000);
mo[1]=0;
int N,M;
scanf("%d%d",&N,&M);
for(int i=1;i<=N;i++)scanf("%d",&a[i]);
int R=0;
for(int l=1;l<=N;l++)
{
while(nowans<=0&&R<N)
{
add(++R,1);
addcnt(R,1);
nowans+=R-l;
}
if(nowans>0)nxt[l]=R;
else nxt[l]=-1;
nowans-=R-l;
addcnt(l,-1);
add(l,-1);
}
for(int i=1;i<=M;i++)
{
int l,r;
scanf("%d%d",&l,&r);
if(nxt[l]!=-1&&nxt[l]<=r)printf("S\n");
else printf("N\n");
}
return 0;
}
边栏推荐
- Double pointer Foundation
- lxml.etree.XMLSyntaxError: Opening and ending tag mismatch: meta line 6 and head, line 8, column 8
- 利用HashMap实现简单缓存
- object serialization
- How can the Solon framework easily obtain the response time of each request?
- Support multi-mode polymorphic gbase 8C database continuous innovation and heavy upgrade
- Romance of programmers on Valentine's Day
- 游戏商城毕业设计
- Acwing 4301. Truncated sequence
- Sword finger offer 53 - ii Missing numbers from 0 to n-1
猜你喜欢
Talking about JVM (frequent interview)
A new micro ORM open source framework
![[to be continued] [UE4 notes] L2 interface introduction](/img/0f/268c852b691bd7459785537f201a41.jpg)
[to be continued] [UE4 notes] L2 interface introduction
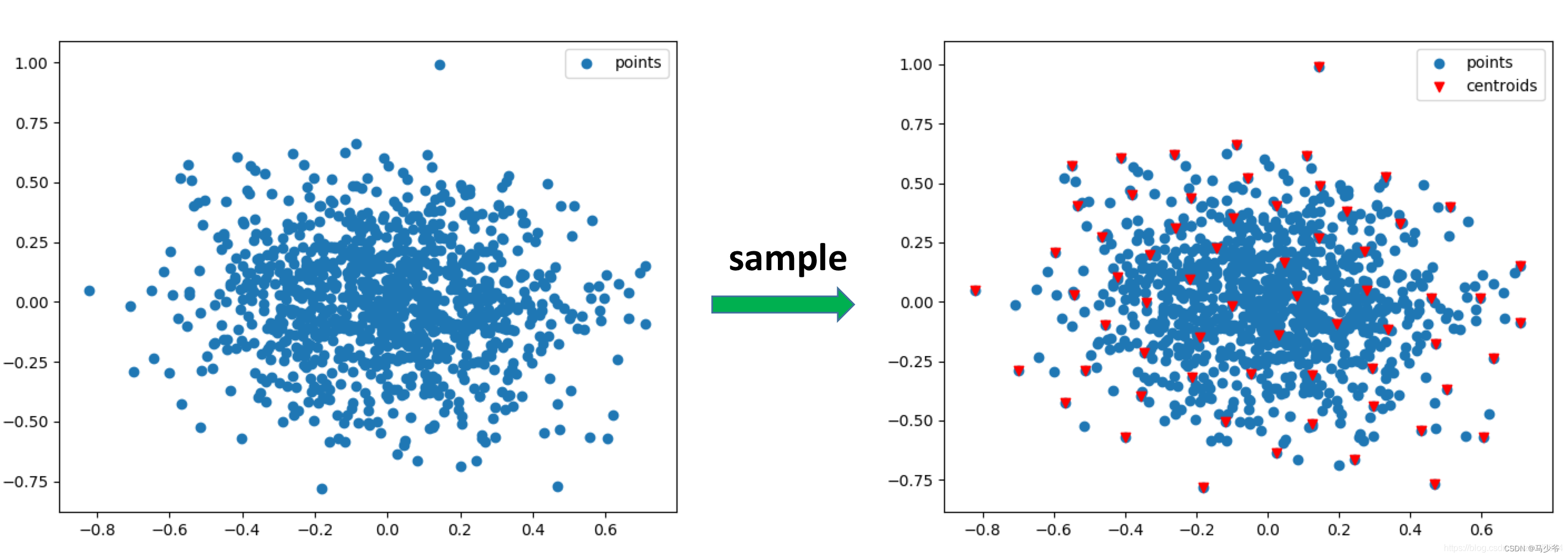
Pointnet++ learning
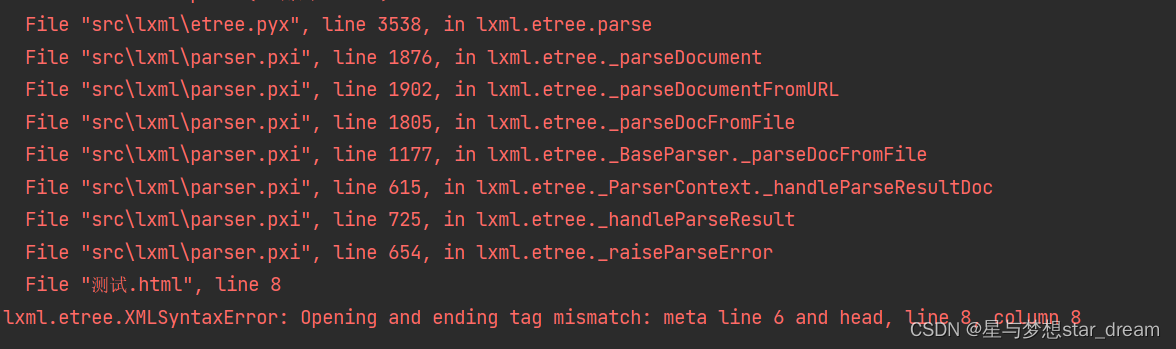
lxml.etree.XMLSyntaxError: Opening and ending tag mismatch: meta line 6 and head, line 8, column 8

Sword finger offer 58 - ii Rotate string left

Binary search basis
Light a light with stm32
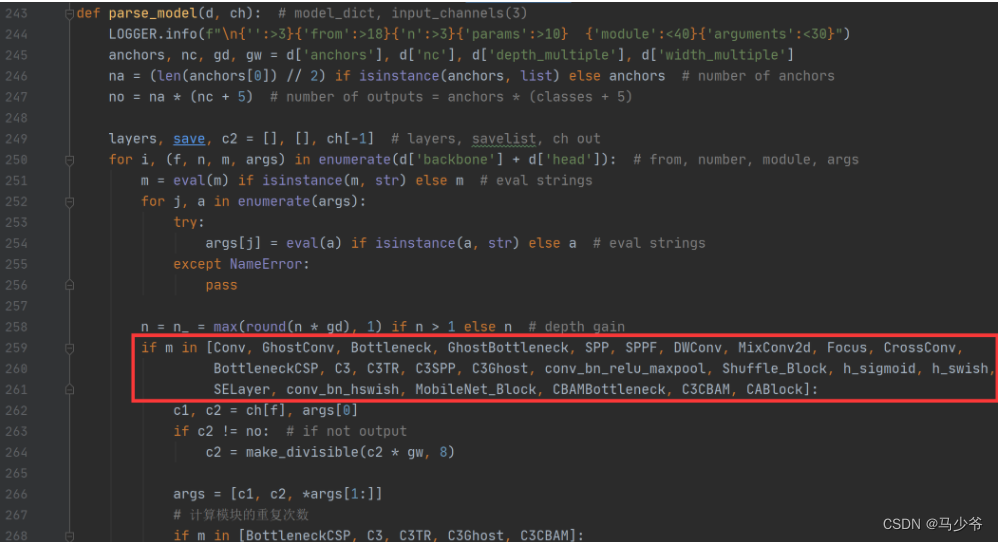
YOLOv5-Shufflenetv2

lxml. etree. XMLSyntaxError: Opening and ending tag mismatch: meta line 6 and head, line 8, column 8
随机推荐
kubeadm系列-01-preflight究竟有多少check
对象的序列化
Sword finger offer 04 Search in two-dimensional array
[es practice] use the native realm security mode on es
Yolov5 adds attention mechanism
记录QT内存泄漏的一种问题和解决方案
Drawing dynamic 3D circle with pure C language
Sword finger offer 53 - I. find the number I in the sorted array
Double pointer Foundation
服务熔断 Hystrix
Zzulioj 1673: b: clever characters???
The number of enclaves
A misunderstanding about the console window
发现一个很好的 Solon 框架试手的教学视频(Solon,轻量级应用开发框架)
Mysql database (I)
剑指 Offer 05. 替换空格
PC寄存器
Web APIs DOM node
【ES实战】ES上的native realm安全方式使用
Haut OJ 2021 freshmen week II reflection summary