当前位置:网站首页>Corridor and bridge distribution (csp-s-2021-t1) popular problem solution
Corridor and bridge distribution (csp-s-2021-t1) popular problem solution
2022-07-05 05:21:00 【Korloa】
Catalog
Option two ( Law finding optimization ):
Code( Don't spray me ^_O_^)(35)( There is something )
Code(55)( I also convinced myself )
Title Description
When a plane arrives at the airport , You can stop at the corridor bridge next to the terminal , You can also stop at the far stand at the edge of the airport . Passengers generally expect to stop at the corridor bridge , Because it saves the trouble of taking the ferry to the terminal . However , Because the number of covered bridges is limited , So such a wish can not always be realized .
The airport is divided into domestic area and international area , Domestic flights can only stop in the domestic area , International flights can only stop in the international zone . Part of the covered bridges belong to the domestic area , The rest of the covered bridges belong to the international zone .
L A new airport has been built in the city , Altogether n A covered bridge . The airport decided , The use of covered bridges follows “ First come first served basis ” Principles , That is, after each plane arrives , If the corresponding area ( At home / The international ) There are also free covered bridges , It stops at the corridor bridge , Otherwise, stop at the far stand ( Assume that the number of far flights is sufficient ). The airport has only one runway , Therefore, there is no case that two planes arrive at the same time .
It is now given that the plane will arrive in the future 、 The moment to leave , Please be responsible for n Corridor bridges are allocated to domestic and international districts , To maximize the number of planes stopping at the corridor bridge .
Input format
The first line of input , Contains three positive integers n,m1,m2, Respectively represents the number of covered bridges 、 Number of domestic flights 、 Number of international flights .
Next m1 That's ok , It's information about domestic flights , The first i Line contains two positive integers a1,i,b1,i, Each represents the arrival of a domestic flight 、 The moment to leave .
Next m2 That's ok , It's information about international flights , The first i Line contains two positive integers a2,i,b2,i, Each represents the arrival of an international flight 、 The moment to leave .
Multiple integers in each line are separated by spaces .
Output format
Output a positive integer , Indicates the maximum number of aircraft that can stop at the corridor bridge .
I/o sample
Input #1 Copy
3 5 4 1 5 3 8 6 10 9 14 13 18 2 11 4 15 7 17 12 16
Output #1 Copy
7
Input #2 Copy
2 4 6 20 30 40 50 21 22 41 42 1 19 2 18 3 4 5 6 7 8 9 10
Output #2 Copy
4
Input #3 Copy
See... In the attachment airport/airport3.in
Output #3 Copy
See... In the attachment airport/airport3.ans
explain / Tips
【 Sample explanation #1】

In the picture , We arrive with 、 The number of pairs at the time of departure represents a plane , Such as (1,5) It means the moment 1 Arrived in 、 moment 5 Leaving the plane ; use √ It means that the plane stops at the corridor bridge , use × It means that the aircraft is parked at a far stand .
Let's take the calculation method of the shaded part in the table as an example , Explain the meaning of this table . In this part , There are 22 A covered bridge ,44 International flights arrive in the same order as the next time :
- First (2, 11) At the moment 2 Arrived in , Stop at the corridor bridge .
- then (4, 15) At the moment 4 Arrived in , Stop at another corridor bridge .
- next (7, 17) At the moment 7 Arrived in , Before this time 22 The plane hasn't left yet 、 Are still occupying the corridor bridge , In the international zone, there are only 22 A covered bridge , So we can only stop at the far stand .
- Last (12, 16) At the moment 12 Arrived in , At this time (2, 11) The plane has left , So there is 1 A free corridor bridge , The plane can stop at the corridor bridge .
According to the calculation results in the table , When the domestic area is allocated 2 A covered bridge 、 International zone allocation 1 When there is a covered bridge , The number of planes stopping at the corridor bridge is the largest , altogether 7 frame .
【 Sample explanation #2】
When the domestic area is allocated 2 A covered bridge 、 International zone allocation 0 When there is a covered bridge , The number of planes stopping at the corridor bridge is the largest , altogether 4 frame , That is, all domestic flights can stop at the corridor bridge .
It should be noted that , The use of corridor bridges in this topic follows “ First come first served basis ” Principles , If there is only 1 A covered bridge , Then it will be flown (1,19) Occupy , Instead of being (3,4)、(5,6)、(7,8)、(9,10) this 4 Planes have been used successively .
Answer key :
Let the time of aircraft landing be Start, The time to leave the corridor bridge is Leave
First set two arrays , Record domestic and foreign flights respectively . Considering that the subject requires first come, first served , Then I naturally think , To press Start Size increasing sort . because STL Medium set The container has the function of automatic sorting , We can save data in this way :
1. Define a structure plane, preservation Start and Leave
struct plane{
int start;
int leave;
};2. Define a plane Type of container line, Save the planes parked in the corridor bridge .
There are two other definitions plane Type of container inside,outside, Respectively represent the sequence of arrival of domestic and foreign aircraft
In addition, in order to visit set The elements in , Also for plane Type defines an iterator ( The pointer )
set <plane> line;
set <plane> inside;
set <plane> outside;
set <plane>::iterator it;3. Because we define set The container is according to start The size of is sorted incrementally , and struct There are two variables in the structure of , We need to be clear about which variable to compare .
bool operator <(const plane a,const plane b){
return a.start<b.start;
} // This function must be placed in struct outside , Otherwise, an error will be reported Now let's think about the core algorithm
Scheme 1 ( simple ):
Ideas :( greedy )
First consider domestic :
Let's assume that there is N A covered bridge , from 1~N Enumerate in sequence when the number of covered bridges is i when , How many planes can we park at most in China . So how to calculate when the number of covered bridges is i when , How many planes can we park at most ?( as follows )
The number of covered bridges in China is i Under the circumstances , set up Ans Indicates the maximum number of planes that can stop
When a plane Z Coming , First of all, the number of planes in the corridor bridge should be updated , about Leave Less than Z.Start( Has flown away before ) The plane , Then take it from Line Delete from , End of traversal Line After all the planes, judge whether there is free space in the corridor bridge , Judgment Line.size()< i , If it is established, the aircraft can be Z Add to Line In line ,Ans++;
It's like this ,Ans The result is that the number of covered bridges is i The maximum number of planes that can dock in the case
Repeat the process , We can define an array Ansin[] To preserve Ansin[i] Of Ans;
The same is true for foreign aircraft , Repeat the process , Define an array Ansout[] To preserve .
You can find , The final required result is :
MAX=Ansin[i]+Ansout[N-i](i=0~N)
Go through it i value .
This method is less efficient , The algorithm I used in the examination room ( Simple minded ), Hung up a lot of points !
Want to see the code at the end of the article , Yes 2~3 A rogue test code (35,50,55 branch ), I think it can be optimized again , There is room for improvement , If you can give me some advice , I would be very grateful .
Next we will focus on another method
Option two ( Law finding optimization ):
The biggest failure of scheme 1 is that many redundant operations are carried out , For example, in enumerating i when inside The first plane in was simulated several times .
therefore , We need to find a way to connect the simulation before and after , If the data established above can be used, try to use , Instead of double counting .
Before , We have been limiting the number of covered bridges i To enumerate in turn , Plan 2, we will no longer limit , It is assumed that the number of covered bridges in the airport is N, But we number it ,1,2.3...i...N It is stipulated that the position with smaller number shall be preferred when the aircraft comes .
Let's take a set of data to simulate :( Only consider domestic )
share 3 A covered bridge ,5 A plane (x,y) Indicates the arrival time of the plane x, Time to leave y
(1 , 12) (13 , 18) (3 , 8) (6 , 15) (4 , 5)
in the light of x Sort
(1,12) (3,8) (4,5) (6,15) (13,18)
1 No. vacant (1,12) It will stop at 1 Number
1 Full number ,2 No. vacant (3,8) It will stop at 2 Number
1,2 Full number , Number three is free (4,5) It will stop at 3 Number
1,2 Full number , No. 3 (4,5) Has left ,3 No. vacant (6,15) It will stop at 3 Number
1 No. has left , Number one is free , Preference 1 (13,19) It will stop at 1 Number
The illustration :
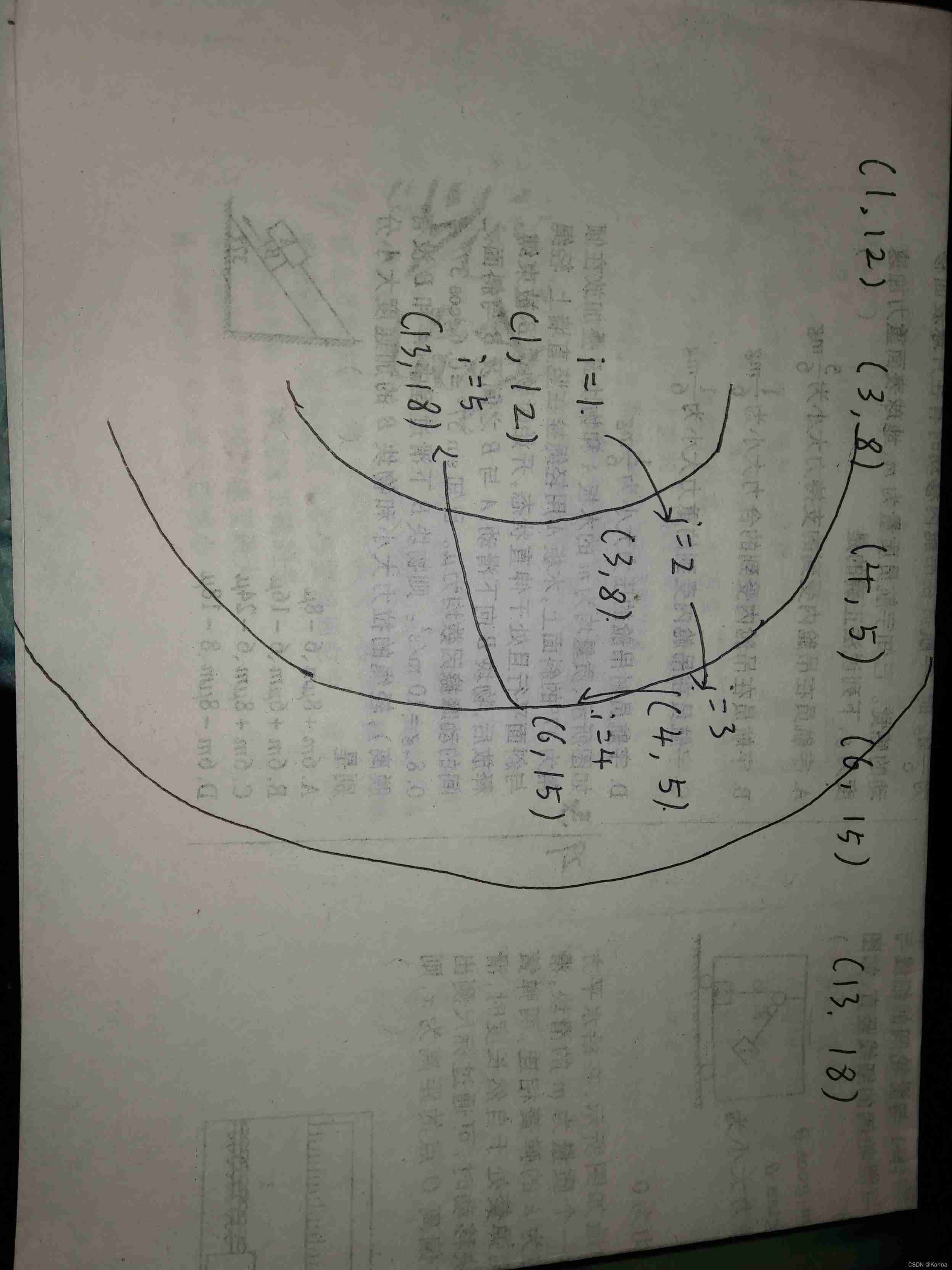
In fact, the above process can be described as specifying the number of covered bridges as 1, The first round of screening records the number of planes that can stop at the corridor bridge s And delete , The rest of the planes form a collection , Record the number of planes that can stop at the corridor bridge s And delete .......... The same goes for foreign countries
You can find :
Ansin[i]=Ansin[i-1]+s
Time complexity O(nlogn)
Over....
Code( Optimize ):
#include<cstdio>
#include<set>
using namespace std;
struct plane{
int start;
int leave;
};
inline int read(){
char c=getchar();
int t=0;
while(c>='0' && c<='9'){
t=(t<<1)+(t<<3)+(c^48);
c=getchar();
}
return t;
}
bool operator <(const plane a,const plane b){
return a.start<b.start;
}
inline void write(int num){
if(num!=0){
write(num/10);
putchar((num%10)^48);
}
}
set <plane> line;
set <plane>::iterator it;
int tot,in,out,res=0,tstart,s;
int ansin[100005];
int ansout[100005];
plane t;
signed main(){
tot=read(),in=read(),out=read();
ansin[0]=0,ansout[0]=0;
for(int i=0;i<in;i++){
t.start=read(),t.leave=read(),line.insert(t);
}
for(int i=1;i<=tot;i++){
tstart=0;
s=0;
while(1){
it=line.lower_bound(plane{tstart,0});
if(it==line.end())break;
tstart=(*it).leave;
line.erase(it);
s++;
}
ansin[i]=ansin[i-1]+s;
}
line.clear();
for(int i=0;i<out;i++){
t.start=read(),t.leave=read(),line.insert(t);
}
for(int i=1;i<=tot;i++){
tstart=0;
s=0;
while(1){
it=line.lower_bound(plane{tstart,0});
if(it==line.end())break;
tstart=(*it).leave;
line.erase(it);
s++;
}
ansout[i]=ansout[i-1]+s;
}
for(int i=0;i<=tot;i++){
if(res<ansin[i]+ansout[tot-i]){
res=ansin[i]+ansout[tot-i];
}
}
write(res);
return 0;
}Tip: I don't know why Luo Gu 21~23 can't make a good living , I spent a chance to run the data by myself , The discovery and answer are still wrong , No more words ~~ In an instant, the Buddha is tied
Code( Don't spray me ^_O_^)(35)( There is something )
#include<iostream>
#include<cstdio>
#include<set>
using namespace std;
int tot,inside,outside;
int neians[10001];
int waians[10001];
int ans=0;
struct plane{
int start;
int leave;
};
bool operator <(const plane a,const plane b){
return a.start<b.start;
}
set<plane> guonei;
set<plane> guowai;
set<plane> line;
set<plane>::iterator itline;
inline int read(){
char c;
c=getchar();
int ans=0;
while(c>='0' && c<='9'){
ans=(ans<<1)+(ans<<3)+(c^48);
c=getchar();
}
return ans;
}
int main(){
neians[0]=0;
waians[0]=0;
plane x;
tot=read();
inside=read();
outside=read();
for(int i=1;i<=inside;i++){
x.start=read();
x.leave=read();
guonei.insert(x);
}
for(int i=1;i<=outside;i++){
x.start=read();
x.leave=read();
guowai.insert(x);
}
for(int i=1;i<=tot;i++){
line.clear();
int aim=0;
set <plane>::iterator it;
for(it=guonei.begin();it!=guonei.end();it++){
if(line.size()<i){
line.insert((*it));
aim++;
}
else{
set <plane>::iterator other;
for(other=line.begin();other!=line.end();other++){
if((*other).leave<(*it).start){
line.erase(other);
line.insert((*it));
aim++;
break;
}
}
}
}
neians[i]=aim;
}
//
for(int i=1;i<=tot;i++){
line.clear();
int aim=0;
set <plane>::iterator it;
for(it=guowai.begin();it!=guowai.end();it++){
if(line.size()<i){
line.insert((*it));
aim++;
}
else{
set <plane>::iterator other;
for(other=line.begin();other!=line.end();other++){
if((*other).leave<(*it).start){
line.erase(other);
line.insert((*it));
aim++;
break;
}
}
}
}
waians[i]=aim;
}
for(int i=0;i<=tot;i++){
if(ans<neians[i]+waians[tot-i]){
ans=neians[i]+waians[tot-i];
}
}
cout<<ans;
return 0;
} Code(55)( I also convinced myself )
#include<cstdio>
#include<set>
using namespace std;
struct plane{
int start;
int leave;
};
bool operator <(const plane a,const plane b){
return a.start<b.start;
}
set <plane> date;
set <plane> far;
plane line;
int ans=0;
int neians[80000];
int waians[80000];
inline int read(){
char c=getchar();
int t=0;
while(c>='0' && c<='9'){
t=(t<<1)+(t<<3)+(c^48);
c=getchar();
}
return t;
}
inline void write(int num){
if(num!=0){
write(num/10);
putchar((num%10)^48);
}
}
int tot,in,out;
plane x;
int main(){
neians[0]=0;
waians[0]=0;
set <plane>::iterator it;
tot=read();
in=read();
out=read();
for(int i=1;i<=in;i++){
x.start=read();
x.leave=read();
date.insert(x);
}
bool choose=true;
for(int i=1;i<=tot;i++){
int aim=0;
if(choose){
if(!date.empty()){
line=*date.begin();
date.erase(date.begin());
it=date.begin();
aim++;
while(1){
if(it==date.end())
break;
if((*it).start>=line.leave){
aim++;
line=*it;
}
else{
far.insert(*it);
}
it++;
}
date.clear();
choose=false;
}
}
///
else{
if(!far.empty()){
line=*far.begin();
far.erase(far.begin());
it=far.begin();
aim++;
while(1){
if(it==far.end())
break;
if((*it).start>=line.leave){
aim++;
line=*it;
}
else{
date.insert(*it);
}
it++;
}
far.clear();
choose=true;
}
}
neians[i]=aim+neians[i-1];
}
date.clear();
far.clear();
for(int i=1;i<=out;i++){
x.start=read();
x.leave=read();
date.insert(x);
}
choose=true;
for(int i=1;i<=tot;i++){
int aim=0;
if(choose){
if(!date.empty()){
line=*date.begin();
date.erase(date.begin());
it=date.begin();
aim++;
while(1){
if(it==date.end())
break;
if((*it).start>=line.leave){
aim++;
line=*it;
}
else{
far.insert(*it);
}
it++;
}
date.clear();
choose=false;
}
}
///
else{
if(!far.empty()){
line=*far.begin();
far.erase(far.begin());
it=far.begin();
aim++;
while(1){
if(it==far.end())
break;
if((*it).start>=line.leave){
aim++;
line=*it;
}
else{
date.insert(*it);
}
it++;
}
far.clear();
choose=true;
}
}
waians[i]=aim+waians[i-1];
}
for(int i=0;i<=tot;i++){
if(ans<neians[i]+waians[tot-i]){
ans=neians[i]+waians[tot-i];
}
}
write(ans);
return 0;
} Gift For you
Here you are “ Riverside Scene at Qingming Festival ”

End~~~
Writing is not easy , Thank you for your support
边栏推荐
- [turn to] MySQL operation practice (III): table connection
- Binary search basis
- Development error notes
- lxml.etree.XMLSyntaxError: Opening and ending tag mismatch: meta line 6 and head, line 8, column 8
- 使用命令符关闭笔记本自带键盘命令
- YOLOv5添加注意力機制
- Warning using room database: schema export directory is not provided to the annotation processor so we cannot export
- Embedded database development programming (VI) -- C API
- 小程序直播+电商,想做新零售电商就用它吧!
- 64 horses, 8 tracks, how many times does it take to find the fastest 4 horses at least
猜你喜欢
Bucket sort
Heap sort summary

Embedded database development programming (V) -- DQL

Page countdown
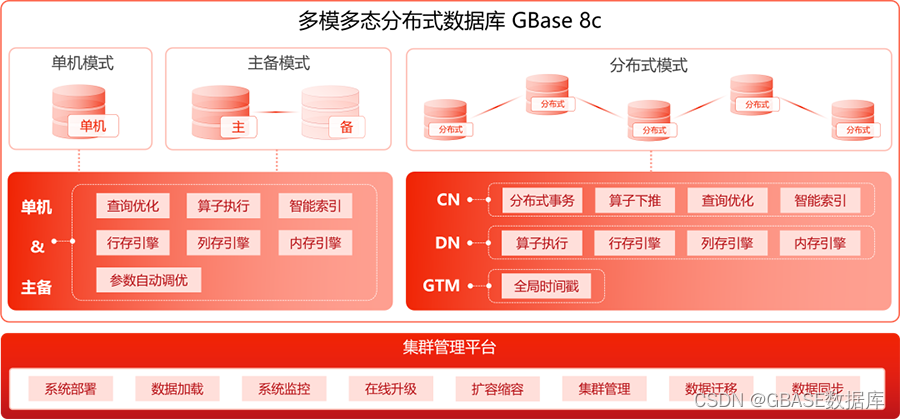
Support multi-mode polymorphic gbase 8C database continuous innovation and heavy upgrade

第六章 数据流建模—课后习题

嵌入式数据库开发编程(六)——C API
Reverse one-way linked list of interview questions

Django reports an error when connecting to the database. What is the reason

Gbase database helps the development of digital finance in the Bay Area
随机推荐
搭建完数据库和网站后.打开app测试时候显示服务器正在维护.
Simple HelloWorld color change
Grail layout and double wing layout
Haut OJ 1245: large factorial of CDs --- high precision factorial
Page countdown
A new micro ORM open source framework
Stm32cubemx (8): RTC and RTC wake-up interrupt
小程序直播+电商,想做新零售电商就用它吧!
【ES实战】ES上的native realm安全方式使用
十年不用一次的JVM调用
To the distance we have been looking for -- film review of "flying house journey"
Web APIs DOM节点
C语言杂谈1
Programmers' experience of delivering takeout
SAP-修改系统表数据的方法
Solon Auth 认证框架使用演示(更简单的认证框架)
ssh免密登录设置及使用脚本进行ssh登录并执行指令
Download and use of font icons
Embedded database development programming (V) -- DQL
质量体系建设之路的分分合合