Bucket sort

The content and code of this article come from 《 Comics algorithm 》.
For the limitation of counting sorting , Bucket sorting makes up , The time complexity is also linear . It is similar to the statistical array created by counting sort , Bucket sorting requires the creation of several buckets to help sort .
So what is called in bucket sorting “ bucket ”, And what is it ？
Every bucket (bucket) It's an interval , It can hold one or more elements .
Suppose there is a non integer sequence as follows ：
4.5,0.84,3.25,2.18,0.5
Let's see how bucket sorting works .
The first step in bucket sorting , It's about creating these buckets , And determine the interval range of each barrel .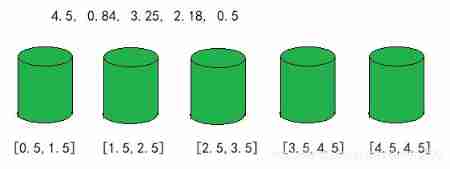

How many barrels need to be built , How to determine the range of the bucket , There are many different ways , The number of buckets we create here is equal to the number of elements in the original sequence . Except that the last bucket contains only the maximum value of the sequence , The interval of each barrel in front , Determined in proportion .
Interval span = ( Maximum - minimum value ) / ( The number of barrels - 1)

The first 2 Step , Traversing the original sequence , Put the elements in the right place and put them in each bucket .

The first 3 Step , Sort the elements inside each bucket separately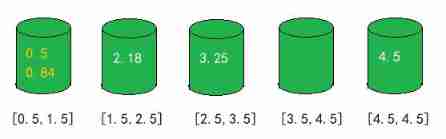

The first 4 Step , Go through all the buckets , Output all elements .
0.5, 0.84, 2.18, 3.25, 4.5
End of sort
java The implementation is as follows ：

	double[] bucketSort(double[] arr) {
    
		// 1. Get the maximum and minimum values of the sequence 
		double max = 0;
		double min = 0;
		for (int i = 0; i < arr.length; i++) {
    
			if (arr[i] > max) {
    
				max = arr[i];
			}
			if (arr[i] < min) {
    
				min = arr[i];
			}
		}

		double d = max - min;

		// 2. Initialize bucket 
		int bucketNum = arr.length;
		ArrayList<LinkedList<Double>> bucketList = new ArrayList<>(bucketNum);
		for (int i = 0; i < bucketNum; i++) {
    
			bucketList.add(new LinkedList<Double>());
		}

		// 3. Traverse the original array , Put each element in a bucket  ( This step )
		for (int i = 0; i < arr.length; i++) {
    
			int num = (int) ((arr[i] - min) * (bucketNum - 1) / d);
			bucketList.get(num).add(arr[i]);
		}

		// 4. Sort the inside of each bucket 
		for (int i = 0; i < bucketList.size(); i++) {
    
			// JDK Adopt the optimized version of merging sorting or merging 
			Collections.sort(bucketList.get(i));
		}

		// 5. Output all elements 
		double[] sortedArr = new double[arr.length];
		int index = 0;
		for (LinkedList<Double> list : bucketList) {
    
			for (double element : list) {
    
				sortedArr[index] = element;
				index++;
			}
		}
		return sortedArr;
	}
	
	@Test
	public void fun1() {
    
		double[] arr = new double[] {
     4.12, 6.421, 0.0023, 3.0, 2.123, 8.122, 4.12, 10.09 };
		double[] sortedArr = bucketSort(arr);
		System.out.println(Arrays.toString(sortedArr));
	}

summary ：
The time complexity of bucket sorting ：O(n), Spatial complexity O(n)
The performance of bucket sorting is not absolutely stable . If the distribution of elements is extremely uneven , In extreme cases , In the first bucket n-1 Elements , There is 1 Elements . At this time, the time complexity will degenerate into O(nlogn), And also created many empty barrels for nothing .

thus it can be seen , There is no absolutely good algorithm , There is no absolutely bad Algorithm , The key depends on the specific scene .