54. 螺旋矩阵 ＆ 59. 螺旋矩阵 II ●●

54. 螺旋矩阵 ●●

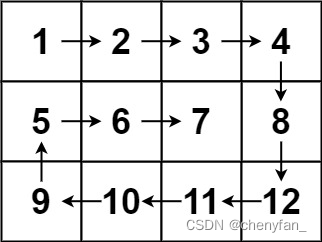
给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

---

输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

• 模拟
  四条边按顺序遍历，移动、判断边界。

class Solution {
    
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
    
        int m = matrix.size();          // m 行
        int n = matrix[0].size();       // n 列
        int top = 0, right = n-1, left = 0, buttom = m-1; //边界索引值
        int numsize = m*n;
        int num = 0;
        vector<int> ans(numsize);
        while(true){
    
            for(int i = left; i <= right; i++){
    
                ans[num++] = matrix[top][i];
            }
            top++;
            if(top>buttom) break;			// 遍历 判断边界

            for(int i = top; i <= buttom; i++){
    
                ans[num++] = matrix[i][right];
            }
            right--;
            if(left>right) break;

            for(int i = right; i >= left;  i--){
    
                ans[num++] = matrix[buttom][i];
            }
            buttom--;
            if(top>buttom) break;

            for(int i = buttom; i >= top; i--){
    
                ans[num++] = matrix[i][left];
            }
            left++;
            if(left>right) break;
        }
        return ans;
    }
};

59. 螺旋矩阵 II ●●

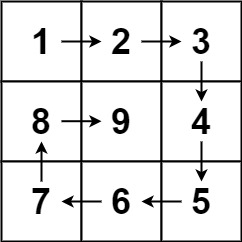
给你一个正整数 n ，生成一个包含 1 到 $n^2$ 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix .

---

输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

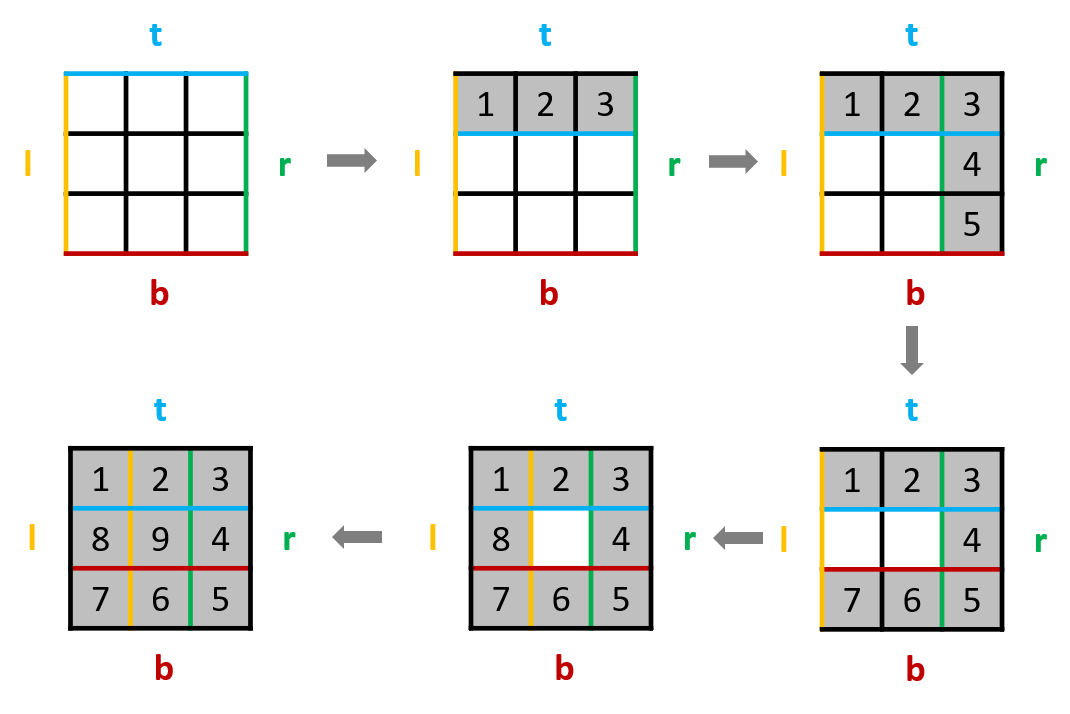
1. 生成一个 n×n 空矩阵 ans，随后模拟整个向内环绕的填入过程：
2. 定义当前左右上下边界 l,r,t,b，初始值 num = 1，迭代终止值 numsize = n * n；
3. 当 num <= numsize 时，始终按照 从左到右 从上到下 从右到左 从下到上 填入顺序循环，每次填入后：
4. 执行 num += 1：得到下一个需要填入的数字；
5. 更新边界：例如从左到右填完后，上边界 t += 1，相当于上边界向内缩 1。
6. 使用 num <= numsize 而不是 l < r || t < b 作为迭代条件，是为了解决当 n 为奇数时，矩阵中心数字无法在迭代过程中被填充的问题。
7. 最终返回 ans 即可。

class Solution {
    
public:
    vector<vector<int>> generateMatrix(int n) {
    
        vector<vector<int>> ans(n, vector<int>(n, 0));
        int up = 0, down = n-1, left = 0, right = n-1;
        int cnt = 1, num = n*n;
        while(cnt <= num){
          // 迭代条件，填充数 <= 格子数
            for(int i = left; i <= right; ++i) ans[up][i] = cnt++;  // 右移 
            ++up;
            for(int i = up; i <= down; ++i) ans[i][right] = cnt++;  // 下移
            --right;
            for(int i = right; i >= left; --i) ans[down][i] = cnt++;    // 左移
            --down;
            for(int i = down; i >= up; --i) ans[i][left] = cnt++;   // 上移
            ++left;
        }
        return ans;
    }
};