Leetcode-6110: number of incremental paths in the grid graph

subject

Topic linking

To give you one m x n Integer grid graph of grid , You can move from a grid to 4 Any lattice adjacent in two directions .

Please return to the grid from arbitrarily Grid departure , achieve arbitrarily lattice , And the number in the path is Strictly increasing Number of paths for . Because the answer could be big , Please correct the results $10^9+7$ Remainder After the return .

If the grids accessed in the two paths are not exactly the same , Then they are regarded as two different paths .

Example 1：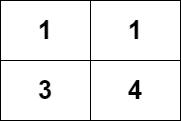

 Input ：grid = [[1,1],[3,4]]
 Output ：8
 explain ： Strictly incremental paths include ：
-  The length is  1  The path of ：[1],[1],[3],[4] .
-  The length is  2  The path of ：[1 -> 3],[1 -> 4],[3 -> 4] .
-  The length is  3  The path of ：[1 -> 3 -> 4] .
 Number of paths is  4 + 3 + 1 = 8 .

Example 2：

 Input ：grid = [[1],[2]]
 Output ：3
 explain ： Strictly incremental paths include ：
-  The length is  1  The path of ：[1],[2] .
-  The length is  2  The path of ：[1 -> 2] .
 Number of paths is  2 + 1 = 3 .

Problem solving

Method 1 ：dfs Memory search

adopt memory Array save , The number of incremental paths per grid
such as memory[i][j], Indicates that the end point is (i,j) Number of incremental paths

class Solution {
    
public:
    const int MOD=1e9+7;
    vector<vector<int>> dirs={
    {
    -1,0},{
    0,-1},{
    1,0},{
    0,1}};
    vector<vector<int>> memory;
    int dfs(vector<vector<int>>& grid,int i,int j){
    
        if(memory[i][j]>0) return memory[i][j];
        memory[i][j]=1;
        for(vector<int>& dir:dirs){
    
            int nx=i+dir[0];
            int ny=j+dir[1];
            if(nx<0||nx>=grid.size()||ny<0||ny>=grid[0].size()||grid[i][j]<=grid[nx][ny]) continue;
            memory[i][j]=(memory[i][j]+dfs(grid,nx,ny))%MOD;
        }
        return memory[i][j];

     }
    int countPaths(vector<vector<int>>& grid) {
    
        int m=grid.size();
        int n=grid[0].size();
        memory.resize(m,vector<int>(n));
        int res=0;
        for(int i=0;i<m;i++){
    
            for(int j=0;j<n;j++){
    
                res=(res+dfs(grid,i,j))%MOD;
            }
        }
        return res;
    }
};

Method 2 ： Dynamic programming （ Overtime ）

dp[i][j][l] Indicates that the grid point is (i,j), The path length is l The number of ,
The purpose of this is because , Only get a length of l-1 Number of paths for , To calculate the length l Number of paths for .
shortcoming ：
However, for example grid[2][3]>grid[2][4]
But every time, we will make repeated comparisons , Traversing (2,3), Will compare with the right , Traversing (2,4) And compare with the left , And can't remember , because dp[i][j][l] It's just l The result of length , Just an intermediate value , Not the end result .

And method one ： It directly saves the number of all incremental paths of each grid point , So it can be memorized .（dfs, Complexity $O(n^2)$）
Method 2 can get the number of each path length , A small amount of data can be obtained by , But it will time out .（ Matrix traversal , Complexity $O(n^3)$）

class Solution {
    
public:
    const int Mod=1e9+7;
    vector<vector<int>> dirs={
    {
    -1,0},{
    0,-1},{
    1,0},{
    0,1}};
    int countPaths(vector<vector<int>>& grid) {
    
        int res=0;
        int m=grid.size();
        int n=grid[0].size();
        int maxPath=m*n;
        vector<vector<vector<int>>> dp(m,vector<vector<int>>(n,vector<int>(m*n+1)));
        for(int i=0;i<m;i++){
    
            for(int j=0;j<n;j++){
    
                dp[i][j][0]=0;
                dp[i][j][1]=1;
                res++;
            }
        }
        for(int l=2;l<=maxPath;l++){
    
            for(int i=0;i<m;i++){
    
                for(int j=0;j<n;j++){
    
                    dp[i][j][l]=0;
                    for(vector<int>& dir:dirs){
    
                        int nx=i+dir[0];
                        int ny=j+dir[1];
                        if(nx>=0&&nx<m&&ny>=0&&ny<n&&grid[i][j]>grid[nx][ny]){
    
                            dp[i][j][l]+=dp[nx][ny][l-1];
                        }
                    }
                    res=(res+dp[i][j][l])%Mod;
                }
            }
            
        }
        return res;
    }
};