当前位置:网站首页>In this indifferent world, light crying
In this indifferent world, light crying
2022-07-05 05:31:00 【solemntee】
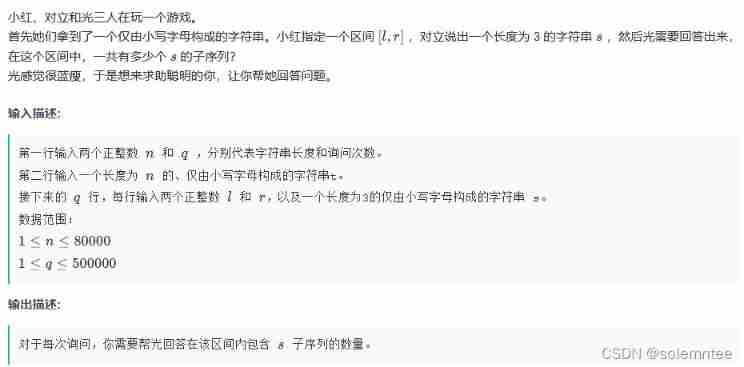
For a substring a b c abc abc, It is easy to find the front i i i Number of bit sequences , Write it down as d p [ i ] [ a ] [ b ] [ c ] dp[i][a][b][c] dp[i][a][b][c]
For a substring a b ab ab, It is easy to find the front i i i Number of bit sequences , Write it down as d p [ i ] [ a ] [ b ] dp[i][a][b] dp[i][a][b]
For a substring a a a, It is easy to find the front i i i Number of bit sequences , Write it down as d p [ i ] [ a ] dp[i][a] dp[i][a]
First consider d p [ r ] [ a ] [ b ] [ c ] − d p [ l − 1 ] [ a ] [ b ] [ c ] dp[r][a][b][c]-dp[l-1][a][b][c] dp[r][a][b][c]−dp[l−1][a][b][c], The number of sequences obtained in this way is two more .
The first category is b c bc bc stay [ l , r ] [l,r] [l,r] Inside , a a a stay [ 1 , l − 1 ] [1,l-1] [1,l−1] Inside
[ l , r ] [l,r] [l,r] Internal b c bc bc The number of sequences is d p [ r ] [ a ] [ b ] − d p [ l − 1 ] [ a ] [ b ] − ( d p [ r ] [ b ] − d p [ l − 1 ] [ b ] ) × d p [ l − 1 ] [ a ] dp[r][a][b]-dp[l-1][a][b]-(dp[r][b]-dp[l-1][b])\times dp[l-1][a] dp[r][a][b]−dp[l−1][a][b]−(dp[r][b]−dp[l−1][b])×dp[l−1][a]
The number of the first category is
( d p [ r ] [ a ] [ b ] − d p [ l − 1 ] [ a ] [ b ] − ( d p [ r ] [ b ] − d p [ l − 1 ] [ b ] ) × d p [ l − 1 ] [ a ] ) × d p [ l − 1 ] [ a ] (dp[r][a][b]-dp[l-1][a][b]-(dp[r][b]-dp[l-1][b])\times dp[l-1][a])\times dp[l-1][a] (dp[r][a][b]−dp[l−1][a][b]−(dp[r][b]−dp[l−1][b])×dp[l−1][a])×dp[l−1][a]
The second type is c c c stay [ l , r ] [l,r] [l,r] Inside , a b ab ab stay [ 1 , l − 1 ] [1,l-1] [1,l−1] Inside
The number of
( d p [ c ] [ r ] − d p [ c ] [ l − 1 ] ) × d p [ a ] [ b ] [ l − 1 ] (dp[c][r]-dp[c][l-1])\times dp[a][b][l-1] (dp[c][r]−dp[c][l−1])×dp[a][b][l−1]
The final answer is
d p [ r ] [ a ] [ b ] [ c ] − d p [ l − 1 ] [ a ] [ b ] [ c ] − ( ( d p [ r ] [ a ] [ b ] − d p [ l − 1 ] [ a ] [ b ] − ( d p [ r ] [ b ] − d p [ l − 1 ] [ b ] ) × d p [ l − 1 ] [ a ] ) × d p [ l − 1 ] [ a ] ) − ( ( d p [ c ] [ r ] − d p [ c ] [ l − 1 ] ) × d p [ a ] [ b ] [ l − 1 ] ) dp[r][a][b][c]-dp[l-1][a][b][c]-((dp[r][a][b]-dp[l-1][a][b]-(dp[r][b]-dp[l-1][b])\times dp[l-1][a])\times dp[l-1][a])-((dp[c][r]-dp[c][l-1])\times dp[a][b][l-1]) dp[r][a][b][c]−dp[l−1][a][b][c]−((dp[r][a][b]−dp[l−1][a][b]−(dp[r][b]−dp[l−1][b])×dp[l−1][a])×dp[l−1][a])−((dp[c][r]−dp[c][l−1])×dp[a][b][l−1])
be aware d p [ n ] [ a ] [ b ] [ c ] dp[n][a][b][c] dp[n][a][b][c] It can be used O ( n × 2 6 2 ) O(n\times26^2) O(n×262) Complexity of complete ( Use the end point to optimize one dimension ), We can ask each group of answers offline O ( n × 2 6 2 + q × C ) O(n\times26^2+q\times C) O(n×262+q×C) complete
#include<bits/stdc++.h>
#define ll long long
using namespace std;
struct node
{
int pos;
ll val;
};
struct query
{
int len,pos,id,f,a,b,c;
};
vector<query>v[80005];
ll Q[500005][8];
ll presum[26][26][26];
ll dp[26][26][3];
char ss[4];
char s[80005];
int main()
{
int n,q;
scanf("%d%d",&n,&q);
scanf("%s",s+1);
for(int i=1;i<=q;i++)
{
// printf("q=%d\n",q);
int l,r;
scanf("%d%d",&l,&r);
scanf("%s",ss+1);
// printf("q=%d\n",q);
/// The length is 3 And
v[l-1].push_back({
3,5,i,-1,ss[1]-'a',ss[2]-'a',ss[3]-'a'});
v[r].push_back({
3,5,i,1,ss[1]-'a',ss[2]-'a',ss[3]-'a'});
/// front 2 Back 1
v[l-1].push_back({
2,1,i,1,ss[1]-'a',ss[2]-'a',ss[3]-'a'});
v[r].push_back({
1,2,i,1,ss[3]-'a',0,0});
v[l-1].push_back({
1,2,i,-1,ss[3]-'a',0,0});
/// front 1 Back 2
v[l-1].push_back({
1,3,i,1,ss[1]-'a',ss[2]-'a',ss[3]-'a'});
v[r].push_back({
2,4,i,1,ss[2]-'a',ss[3]-'a',0});
v[l-1].push_back({
2,4,i,-1,ss[2]-'a',ss[3]-'a',0});
v[r].push_back({
1,6,i,1,ss[3]-'a',0,0});
v[l-1].push_back({
1,6,i,-1,ss[3]-'a',0,0});
v[l-1].push_back({
1,7,i,1,ss[2]-'a',0,0});
// printf("q=%d\n",q);
}
for(int j=0;j<=25;j++)
for(int k=0;k<=25;k++)dp[j][k][0]=1;
for(int i=1;i<=n;i++)
{
for(int j=0;j<=25;j++)
for(int k=0;k<=25;k++)
{
presum[j][k][s[i]-'a']+=dp[j][k][2];
if(s[i]-'a'==k)dp[j][k][2]+=dp[j][k][1];
if(s[i]-'a'==j)dp[j][k][1]+=dp[j][k][0];
}
for(auto [len,pos,id,f,a,b,c]:v[i])
{
// printf("len=%d pos=%d id=%d f=%d a=%d b=%d c=%d \n",len,pos,id,f,a,b,c);
if(len==1)Q[id][pos]+=f*dp[a][0][1];
else if(len==2)Q[id][pos]+=f*dp[a][b][2];
else if(len==3)Q[id][pos]+=f*presum[a][b][c];
}
}
for(int i=1;i<=q;i++)printf("%lld\n",Q[i][5]-Q[i][1]*Q[i][2]-Q[i][3]*(Q[i][4]-Q[i][6]*Q[i][7]));
return 0;
}
边栏推荐
- After setting up the database and website When you open the app for testing, it shows that the server is being maintained
- 数仓项目的集群脚本
- [es practice] use the native realm security mode on es
- [interval problem] 435 Non overlapping interval
- Talking about JVM (frequent interview)
- MySQL数据库(一)
- Codeforces Round #716 (Div. 2) D. Cut and Stick
- 过拟合与正则化
- Palindrome (csp-s-2021-palin) solution
- Solon Auth 认证框架使用演示(更简单的认证框架)
猜你喜欢

【实战技能】非技术背景经理的技术管理

Chapter 6 data flow modeling - after class exercises
![[interval problem] 435 Non overlapping interval](/img/a3/2911ee72635b93b6430c2efd05ec9a.jpg)
[interval problem] 435 Non overlapping interval
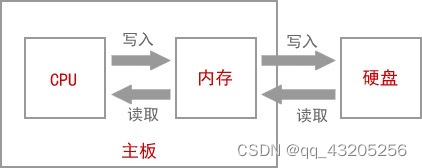
C language Essay 1
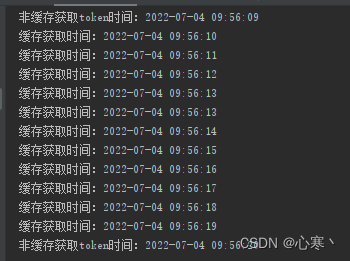
利用HashMap实现简单缓存
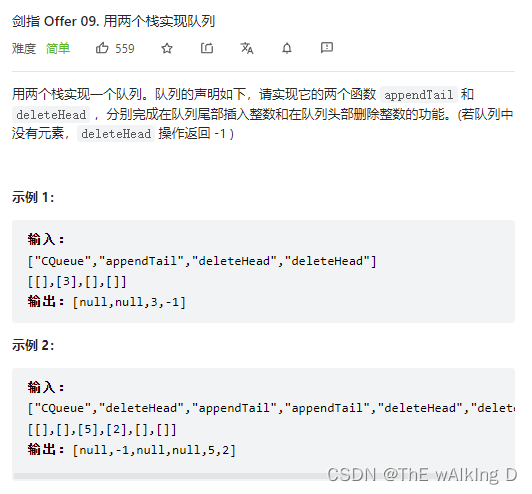
Sword finger offer 09 Implementing queues with two stacks
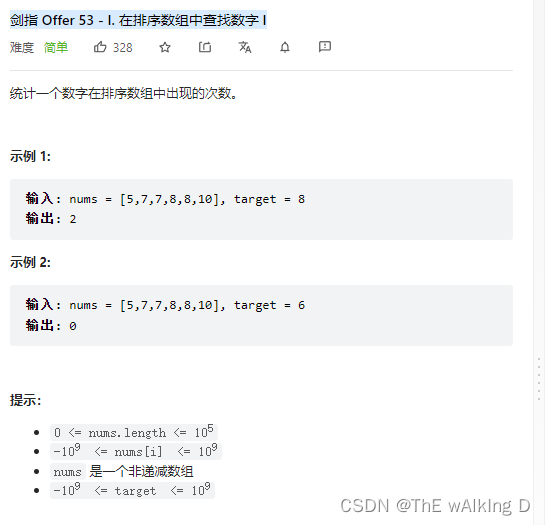
Sword finger offer 53 - I. find the number I in the sorted array

个人开发的渗透测试工具Satania v1.2更新

YOLOv5添加注意力機制
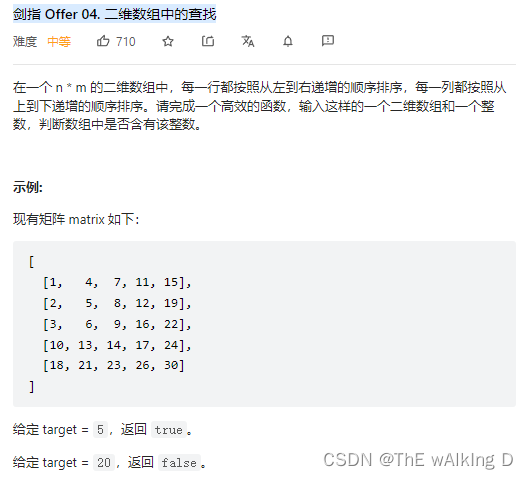
Sword finger offer 04 Search in two-dimensional array
随机推荐
Cluster script of data warehouse project
Sword finger offer 09 Implementing queues with two stacks
Time complexity and space complexity
A misunderstanding about the console window
[speed pointer] 142 circular linked list II
剑指 Offer 53 - I. 在排序数组中查找数字 I
Fragment addition failed error lookup
How can the Solon framework easily obtain the response time of each request?
剑指 Offer 05. 替换空格
Zheng Qing 21 ACM is fun. (3) part of the problem solution and summary
剑指 Offer 09. 用两个栈实现队列
Yolov5 ajouter un mécanisme d'attention
lxml. etree. XMLSyntaxError: Opening and ending tag mismatch: meta line 6 and head, line 8, column 8
Improvement of pointnet++
Sword finger offer 53 - I. find the number I in the sorted array
To the distance we have been looking for -- film review of "flying house journey"
kubeadm系列-01-preflight究竟有多少check
[to be continued] [depth first search] 547 Number of provinces
Palindrome (csp-s-2021-palin) solution
利用HashMap实现简单缓存