当前位置:网站首页>Educational codeforces round 109 (rated for Div. 2) C. robot collisions D. armchairs
Educational codeforces round 109 (rated for Div. 2) C. robot collisions D. armchairs
2022-07-05 05:30:00 【solemntee】
First say D
I was going to find a prefix and optimization d p dp dp Examples of , I can't find the simple one all the time , Hard too hard . Open today d i v div div, Yo roar , Here comes the example .
The title means to have n n n A seat m m m personal ( m < n / 2 ) (m<n/2) (m<n/2) Sit in some positions , Now it is required that the original seats of these sitting people be empty , Let these people sit in other seats , Ask the minimum value of the sum of the moving distances .
The state of this question is very muscular memory , d p [ i ] [ j ] dp[i][j] dp[i][j] It means the first one i Sit down alone j An empty seat , And before i The minimum moving distance of an individual perfect match .
Let's consider the transfer
d p [ i ] [ j ] = m i n k = 1 , 2 , . . , j − 1 ( d p [ i − 1 ] [ k ] ) + a b s ( d i s 1 [ i ] − d i s 0 [ j ] ) dp[i][j]=min_{k=1,2,..,j-1}(dp[i-1][k])+abs(dis1[i]-dis0[j]) dp[i][j]=mink=1,2,..,j−1(dp[i−1][k])+abs(dis1[i]−dis0[j])
We think of a O(n^3) Of dp, And then we found out m i n k = 1 , 2 , . . , j − 1 ( d p [ i − 1 ] [ k ] ) min_{k=1,2,..,j-1}(dp[i-1][k]) mink=1,2,..,j−1(dp[i−1][k])
Yes. O ( n ) O(n) O(n) Pretreated , So this d p dp dp One dimension is optimized , Turned into O ( n 2 ) O(n^2) O(n2), We are beautiful A It fell off D topic .
#include<bits/stdc++.h>
using namespace std;
int cnt1=0,cnt0=0;
int dis1[5005],dis0[5005];
int dp[5005][5005];
int minn[5005];
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
int t;
scanf("%d",&t);
if(t==1)dis1[++cnt1]=i;
if(t==0)dis0[++cnt0]=i;
}
for(int i=0;i<=cnt1;i++)
for(int j=0;j<=cnt0;j++)
dp[i][j]=1e9;
for(int i=1;i<=cnt0;i++)dp[1][i]=abs(dis1[1]-dis0[i]);
for(int j=0;j<=cnt0;j++)minn[j]=1e9;
for(int j=1;j<=cnt0;j++)minn[j]=min(minn[j-1],dp[1][j]);
for(int i=2;i<=cnt1;i++)
{
for(int j=i;j<=cnt0;j++)if(minn[j-1]!=1e9)dp[i][j]=minn[j-1]+abs(dis1[i]-dis0[j]);
for(int j=0;j<=cnt0;j++)minn[j]=1e9;
for(int j=1;j<=cnt0;j++)minn[j]=min(minn[j-1],dp[i][j]);
}
int minn=1e9;
if(cnt1==0)printf("0\n");
else
{
for(int i=1;i<=cnt0;i++)
{
minn=min(minn,dp[cnt1][i]);
}
printf("%d\n",minn);
}
return 0;
}
Besides, C
C It's similar to the problem of ants walking , Go to the two boundaries will rebound , Two ants are On the hour Collision will kill , Ask for the time when each ant dies .
First of all, there is a small conclusion , Two ants will collide at the whole point if and only if their parity is the same .
So we can separate the ants in odd positions from those in even positions .
We look from left to right on the number axis , We know the leftmost
< − < − <-<- <−<−
They must have collided with each other , We can get rid of them
So the leftmost side becomes like this
− > -> −>
Or so < − − > <- -> <−−>
Then we found that if there are two adjacent ants walking opposite , They must have collided with each other , So we use a monotone stack to maintain this relationship , If the top of the stack and I are both left , Then eliminate , If it's all right , So go to the stack , If opposite , Then eliminate . So you get a monotonous stack , Then we will reverse the operation again , It's done , In fact, I think there is only 1500 branch , So put it in C There's nothing wrong with that , But the author may overestimate your code ability , So lead to C Too little .
#include<bits/stdc++.h>
using namespace std;
struct edge
{
int id,dis,dir;
bool operator < (const edge &ths)const
{
return dis<ths.dis;
};
}a[300005];
stack<edge>q0,q1;
int ans[300005];
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int n,m;
while(!q0.empty())q0.pop();
while(!q1.empty())q1.pop();
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i].dis);
a[i].id=i;
}
for(int i=1;i<=n;i++)
{
char c[2];
scanf("%s",c);
if(c[0]=='L')a[i].dir=1;
if(c[0]=='R')a[i].dir=0;
}
sort(a+1,a+1+n);
memset(ans,-1,sizeof(ans));
for(int i=1;i<=n;i++)
{
if(a[i].dis%2==0)
{
if(q0.empty())q0.push(a[i]);
else
{
edge p=q0.top();
if(p.dir==1&&a[i].dir==1)
{
q0.pop();
ans[p.id]=p.dis+abs(p.dis-a[i].dis)/2;
ans[a[i].id]=ans[p.id];
}
else if(p.dir==0&&a[i].dir==1)
{
q0.pop();
ans[p.id]=abs(p.dis-a[i].dis)/2;
ans[a[i].id]=ans[p.id];
}
else
{
q0.push(a[i]);
}
}
}
if(a[i].dis%2==1)
{
if(q1.empty())q1.push(a[i]);
else
{
edge p=q1.top();
if(p.dir==1&&a[i].dir==1)
{
q1.pop();
ans[p.id]=p.dis+abs(p.dis-a[i].dis)/2;
ans[a[i].id]=ans[p.id];
}
else if(p.dir==0&&a[i].dir==1)
{
q1.pop();
ans[p.id]=abs(p.dis-a[i].dis)/2;
ans[a[i].id]=ans[p.id];
}
else
{
q1.push(a[i]);
}
}
}
// printf("1\n");
}
while(q0.size()>=2)
{
edge p2=q0.top();
q0.pop();
edge p1=q0.top();
q0.pop();
// printf("p1 %d p2 %d %d %d\n\n",p1.dis,p2.dis,p1.dir,p2.dir);
if(p1.dir==0&&p2.dir==0)
{
ans[p1.id]=(m-p2.dis)+abs(p1.dis-p2.dis)/2;
ans[p2.id]=ans[p1.id];
}
else if(p1.dir==1&&p2.dir==0)
{
ans[p1.id]=((m-p2.dis)+p1.dis+m)/2;
ans[p2.id]=ans[p1.id];
}
}
while(q1.size()>=2)
{
edge p2=q1.top();
q1.pop();
edge p1=q1.top();
q1.pop();
// printf("p1 %d p2 %d %d %d\n\n",p1.dis,p2.dis,p1.dir,p2.dir);
if(p1.dir==0&&p2.dir==0)
{
ans[p1.id]=(m-p2.dis)+abs(p1.dis-p2.dis)/2;
ans[p2.id]=ans[p1.id];
}
else if(p1.dir==1&&p2.dir==0)
{
ans[p1.id]=((m-p2.dis)+p1.dis+m)/2;
ans[p2.id]=ans[p1.id];
}
}
for(int i=1;i<=n;i++)printf("%d ",ans[i]);
printf("\n");
}
return 0;
}
边栏推荐
- TF-A中的工具介绍
- 【ES实战】ES上的native realm安全方式使用
- SAP method of modifying system table data
- 动漫评分数据分析与可视化 与 IT行业招聘数据分析与可视化
- [to be continued] [UE4 notes] L2 interface introduction
- Maximum number of "balloons"
- Csp-j-2020-excellent split multiple solutions
- SDEI初探-透过事务看本质
- Romance of programmers on Valentine's Day
- 记录QT内存泄漏的一种问题和解决方案
猜你喜欢
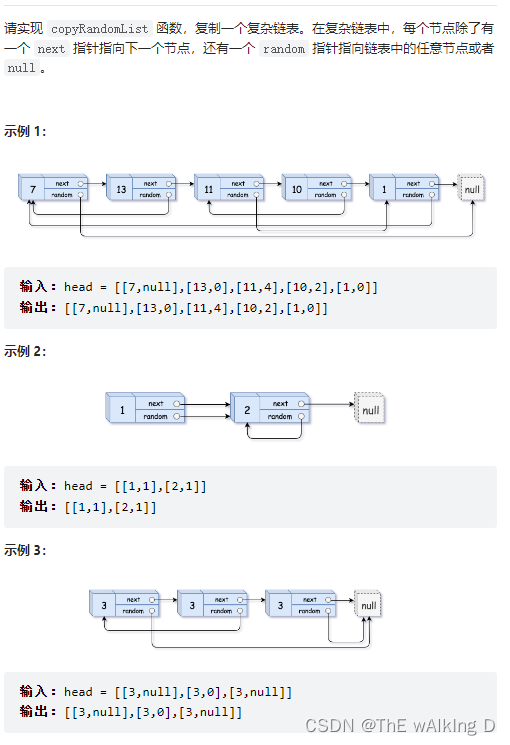
剑指 Offer 35.复杂链表的复制

Hang wait lock vs spin lock (where both are used)
![[轉]: OSGI規範 深入淺出](/img/54/d73a8d3e375dfe430c2eca39617b9c.png)
[轉]: OSGI規範 深入淺出
![[depth first search] 695 Maximum area of the island](/img/08/cfff4aec667216e4f146205a12c13f.jpg)
[depth first search] 695 Maximum area of the island
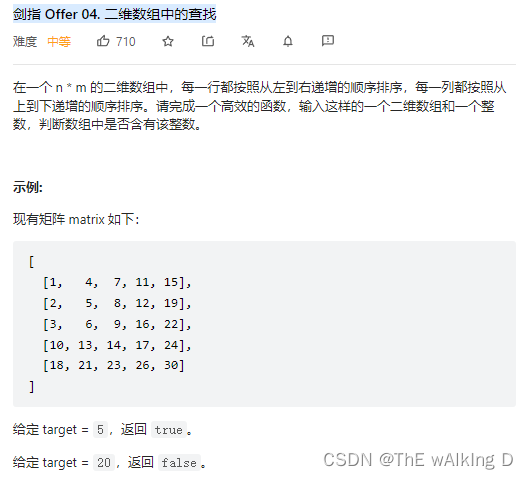
Sword finger offer 04 Search in two-dimensional array
![[turn to] MySQL operation practice (I): Keywords & functions](/img/b1/8b843014f365b786e310718f669043.png)
[turn to] MySQL operation practice (I): Keywords & functions

Sword finger offer 58 - ii Rotate string left
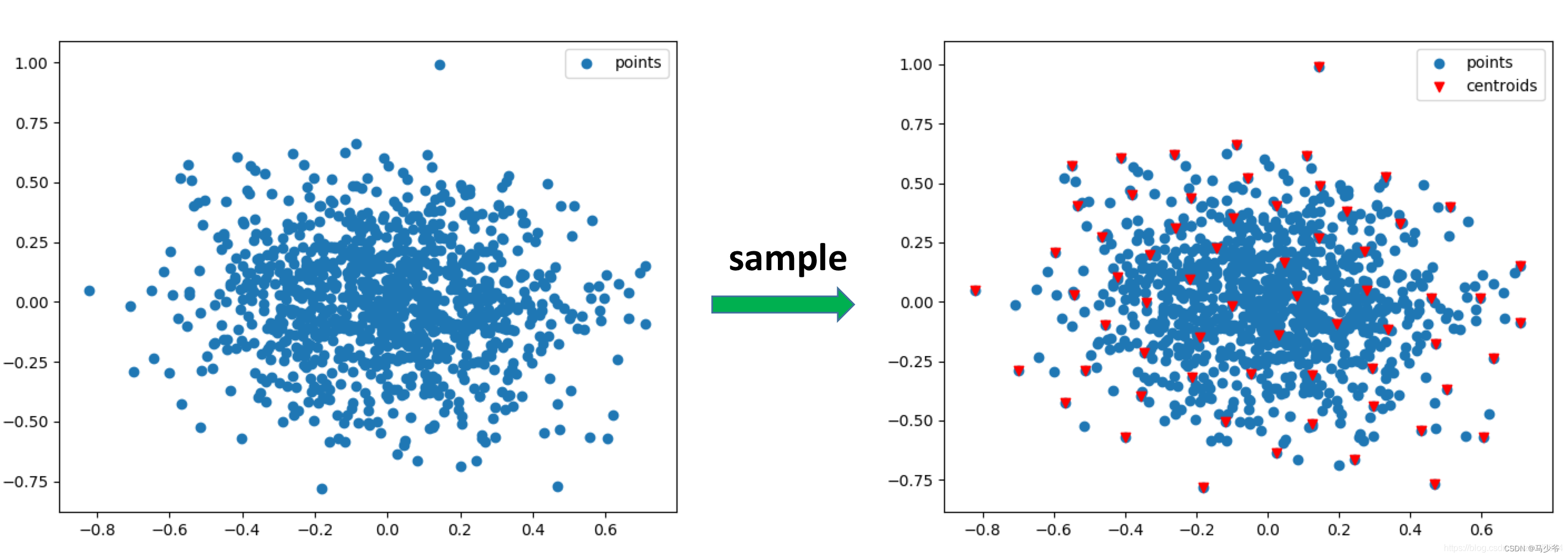
Pointnet++ learning
On-off and on-off of quality system construction
Fragment addition failed error lookup
随机推荐
[轉]: OSGI規範 深入淺出
A preliminary study of sdei - see the essence through transactions
每日一题-无重复字符的最长子串
To be continued] [UE4 notes] L4 object editing
搭建完数据库和网站后.打开app测试时候显示服务器正在维护.
[to be continued] [UE4 notes] L3 import resources and project migration
Haut OJ 1350: choice sends candy
MySQL数据库(一)
[to be continued] [depth first search] 547 Number of provinces
注解与反射
PC寄存器
YOLOv5-Shufflenetv2
[binary search] 34 Find the first and last positions of elements in a sorted array
Support multi-mode polymorphic gbase 8C database continuous innovation and heavy upgrade
[turn to] MySQL operation practice (III): table connection
SSH password free login settings and use scripts to SSH login and execute instructions
[to be continued] [UE4 notes] L1 create and configure items
【Jailhouse 文章】Look Mum, no VM Exits
After setting up the database and website When you open the app for testing, it shows that the server is being maintained
On-off and on-off of quality system construction