当前位置:网站首页>20220701 barbarat lemma proof
20220701 barbarat lemma proof
2022-07-04 08:48:00 【Can you eat spicy food】
(Barbalat lemma )
If differentiable function f ( t ) f(t) f(t), When t → ∞ t \rightarrow \infty t→∞ There is a finite limit , And f ˙ ( t ) \dot{f}(t) f˙(t) Uniformly continuous , So when t → ∞ t \rightarrow \infty t→∞ when , f ˙ ( t ) → 0 \dot{f}(t) \rightarrow 0 f˙(t)→0.
prove ( Reduction to absurdity ):
Suppose that t → ∞ t \rightarrow \infty t→∞ when , f ˙ ( t ) → 0 \dot{f}(t) \rightarrow 0 f˙(t)→0 Don't set up , Then there is an increasing infinite sequence { t n } n ∈ N \{t_n\}_{n\in\mathbb{N}} { tn}n∈N bring (1) When n → ∞ n \rightarrow \infty n→∞ Yes t n → ∞ t_n \rightarrow \infty tn→∞ ;(2) ∣ f ˙ ( t n ) ∣ ⩾ ϵ > 0 |\dot{f}(t_n) | \geqslant \epsilon>0 ∣f˙(tn)∣⩾ϵ>0 For all { t n } \{t_n\} { tn}.
consider f ˙ ( t ) \dot{f}(t) f˙(t) Consistent continuity of , according to ϵ − δ \epsilon-\delta ϵ−δ theory , There is a certain ϵ > 0 \epsilon>0 ϵ>0 , Such that for all n ∈ N n\in\mathbb{N} n∈N and all t ∈ R t \in \mathbb{R} t∈R, When
∣ t n − t ∣ ⩽ δ |t_n -t|\leqslant\delta ∣tn−t∣⩽δ Then there are ∣ f ˙ ( t n ) − f ˙ ( t ) ∣ ≤ ε 2 \left|\dot{f}\left(t_{n}\right)-\dot{f}(t)\right| \leq \frac{\varepsilon}{2} ∣∣∣f˙(tn)−f˙(t)∣∣∣≤2ε
therefore , For all t ∈ [ t n , t n + δ ] t\in[t_n,t_n+\delta] t∈[tn,tn+δ], And all n ∈ N n\in\mathbb{N} n∈N, Yes ∣ f ˙ ( t ) ∣ = ∣ f ˙ ( t n ) − ( f ˙ ( t n ) − f ˙ ( t ) ) ∣ ⩾ ∣ f ˙ ( t n ) ∣ − ∣ f ˙ ( t n ) − f ˙ ( t ) ∣ ⩾ ε − ε 2 = ε 2 \begin{aligned} |\dot{f}(t)| =\left|\dot{f}\left(t_{n}\right)-\left(\dot{f}\left(t_{n}\right)-\dot{f}(t)\right)\right| \geqslant \left|\dot{f}\left(t_{n}\right)\right|-\left|\dot{f}\left(t_{n}\right)-\dot{f}(t)\right| \geqslant \varepsilon-\frac{\varepsilon}{2}=\frac{\varepsilon}{2} \end{aligned} ∣f˙(t)∣=∣∣∣f˙(tn)−(f˙(tn)−f˙(t))∣∣∣⩾∣∣∣f˙(tn)∣∣∣−∣∣∣f˙(tn)−f˙(t)∣∣∣⩾ε−2ε=2ε therefore , For all n ∈ N n\in\mathbb{N} n∈N, Yes ∣ ∫ 0 t n + δ f ˙ ( t ) d t − ∫ 0 t n f ˙ ( t ) d t ∣ = ∣ ∫ t n t n + δ f ˙ ( t ) d t ∣ = ∫ t n t n + δ ∣ f ˙ ( t ) ∣ d t ≥ ε δ 2 > 0 \left|\int_{0}^{t_{n}+\delta} \dot{f}(t) d t-\int_{0}^{t_{n}} \dot{f}(t) d t\right|=\left|\int_{t_{n}}^{t_{n}+\delta} \dot{f}(t) d t\right|=\int_{t_{n}}^{t_{n}+\delta}|\dot{f}(t)| d t \geq \frac{\varepsilon \delta}{2}>0 ∣∣∣∣∣∫0tn+δf˙(t)dt−∫0tnf˙(t)dt∣∣∣∣∣=∣∣∣∣∣∫tntn+δf˙(t)dt∣∣∣∣∣=∫tntn+δ∣f˙(t)∣dt≥2εδ>0
According to the hypothesis , ∫ 0 ∞ f ˙ ( t ) d t < β \int_0^\infty \dot f(t) dt<\beta ∫0∞f˙(t)dt<β There is , therefore , When n → ∞ n\rightarrow \infty n→∞, ∣ ∫ 0 t n + δ f ˙ ( t ) d t − ∫ 0 t n f ˙ ( t ) d t ∣ → 0 \left|\int_{0}^{t_{n}+\delta} \dot{f}(t) d t-\int_{0}^{t_{n}} \dot{f}(t) d t\right| \rightarrow 0 ∣∣∣∣∣∫0tn+δf˙(t)dt−∫0tnf˙(t)dt∣∣∣∣∣→0, Conflict with the above formula , Therefore, the counter evidence method can prove , When t → ∞ t \rightarrow \infty t→∞ when , f ˙ ( t ) → 0 \dot{f}(t) \rightarrow 0 f˙(t)→0.
边栏推荐
- 转:优秀的管理者,关注的不是错误,而是优势
- What is inner connection and outer connection? What are the uses and benefits
- Collections in Scala
- Azure ad domain service (II) configure azure file share disk sharing for machines in the domain service
- L1 regularization and L2 regularization
- Cancel ctrl+alt+delete when starting up
- 力扣今日题-1200. 最小绝对差
- 老掉牙的 synchronized 锁优化,一次给你讲清楚!
- How to pass custom object via intent in kotlin
- User login function: simple but difficult
猜你喜欢
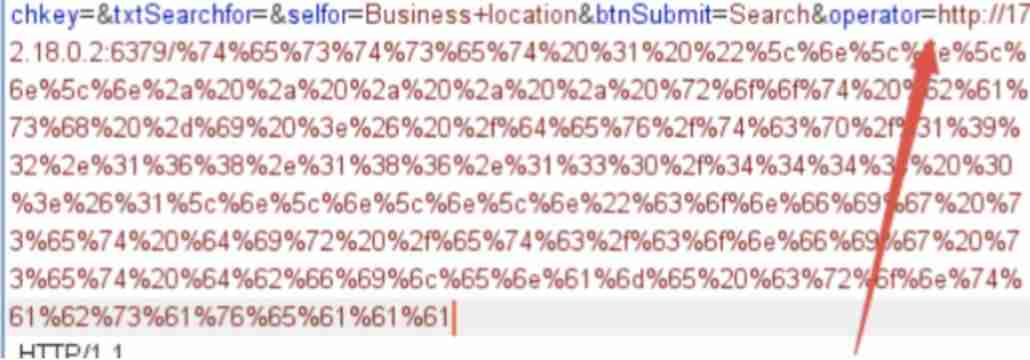
SSRF vulnerability exploitation - attack redis
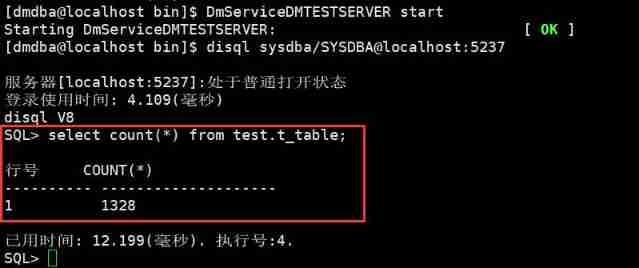
DM8 database recovery based on point in time

Guanghetong's high-performance 4g/5g wireless module solution comprehensively promotes an efficient and low-carbon smart grid
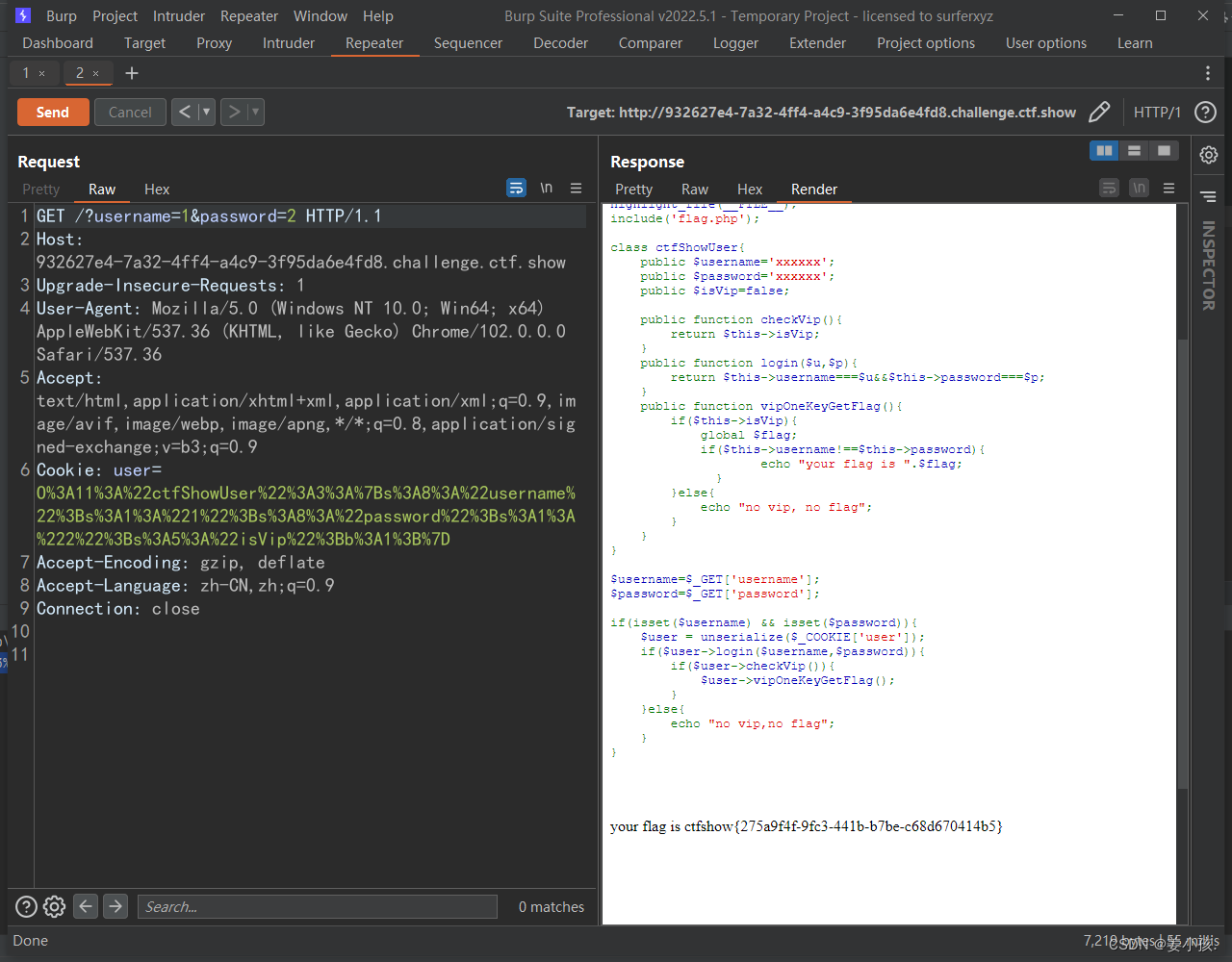
ctfshow web255 web 256 web257

随机事件的关系与运算

ctfshow web255 web 256 web257

How does Xiaobai buy a suitable notebook

What if I forget the router password
How to re enable local connection when the network of laptop is disabled
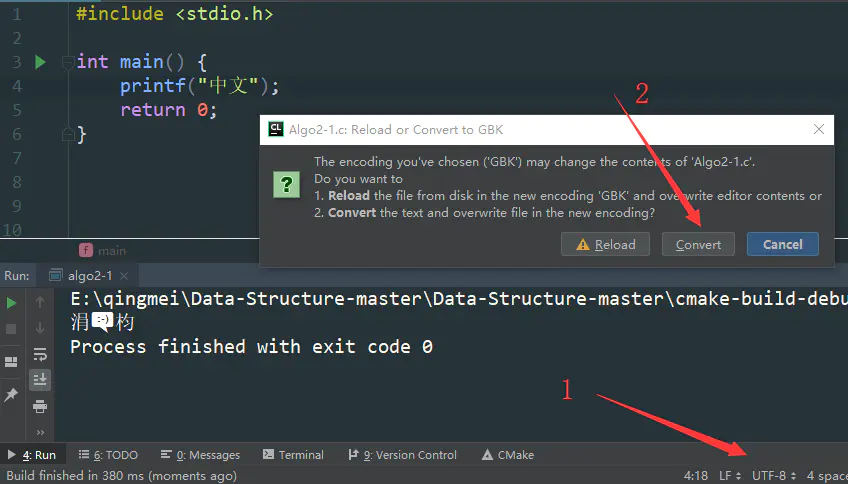
CLion-控制台输出中文乱码
随机推荐
ES6 summary
【无标题】转发最小二乘法
What if the wireless network connection of the laptop is unavailable
swatch
[Chongqing Guangdong education] National Open University spring 2019 455 logistics practice reference questions
1211 or chicken and rabbit in the same cage
awk从入门到入土(5)简单条件匹配
awk从入门到入土(15)awk执行外部命令
Go zero micro service practical series (IX. ultimate optimization of seckill performance)
NewH3C——ACL
Relationship and operation of random events
deno debugger
Internal learning
awk从入门到入土(8)数组
C语言-入门-基础-语法-[变量,常亮,作用域](五)
Flutter integrated amap_ flutter_ location
SSRF vulnerability exploitation - attack redis
The map set type is stored in the form of key value pairs, and the iterative traversal is faster than the list set
2022 gas examination registration and free gas examination questions
HMS core helps baby bus show high-quality children's digital content to global developers