当前位置:网站首页>Li Kou leetcode 280 weekly match
Li Kou leetcode 280 weekly match
2022-07-06 16:41:00 【Dog egg L】
obtain 0 The number of operations
Here are two for you non-negative Integers num1 and num2 .
Each step operation in , If num1 >= num2 , You have to use num1 reduce num2 ; otherwise , You have to use num2 reduce num1 .
for example ,num1 = 5 And num2 = 4 , Should use the num1 reduce num2 , therefore , obtain num1 = 1 and num2 = 4 . However , If num1 = 4 And num2 = 5 , After one step operation , obtain num1 = 4 and num2 = 1 .
Return to make num1 = 0 or num2 = 0 Of Operands .
Input :num1 = 2, num2 = 3 Output :3 explain :
- operation 1 :num1 = 2 ,num2 = 3 . because num1 < num2 ,num2 reduce num1 obtain num1 = 2 ,num2 = 3 - 2 = 1 .
- operation 2 :num1 = 2 ,num2 = 1 . because num1 > num2 ,num1 reduce num2 .
- operation 3 :num1 = 1 ,num2 = 1 . because num1 == num2 ,num1 reduce num2 . here num1 = 0 ,num2 = 1 . because num1 == 0 , No more action is required . So the total operand is 3 .
Input :num1 = 10, num2 = 10 Output :1 explain :
- operation 1 :num1 = 10 ,num2 = 10 . because num1 == num2 ,num1 reduce num2 obtain num1 = 10 - 10 = 0 . here num1 = 0 ,num2 = 10 . because num1 == 0 , No more action is required .
So the total operand is 1 .
0 <= num1, num2 <= 105
class Solution {
public:
int countOperations(int num1, int num2) {
int ans=0;
while(num1&&num2)
{
if(num1>num2)
{
num1-=num2;
ans++;
}
else
{
num2-=num1;
ans++;
}
}
return ans;
}
};
The minimum number of operands to make an array an alternating array
I'll give you a subscript from 0 Starting array nums , The array consists of n It's made up of four positive integers .
If the following conditions are met , The array nums It's a Alternating array :
nums[i - 2] == nums[i] , among 2 <= i <= n - 1 .
nums[i - 1] != nums[i] , among 1 <= i <= n - 1 .
In one step operation in , You can choose the subscript i And will nums[i] change by any Positive integer .
Returns the that makes the array an alternating array The minimum number of operands .
Example 1:
Input :nums = [3,1,3,2,4,3] Output :3 explain : One way to turn an array into an alternating array is to convert the array to [3,1,3,1,3,1]
. under these circumstances , The operands are 3 . Can prove that , Operands are less than 3 Under the circumstances , Cannot make an array into an alternating array .
Example 2:
Input :nums = [1,2,2,2,2] Output :2 explain : One way to turn an array into an alternating array is to convert the array to [1,2,1,2,1].
under these circumstances , The operands are 2 . Be careful , Array cannot be converted to [2,2,2,2,2] . Because in this case ,nums[0] ==
nums[1], The condition of alternating array is not satisfied .
1 <= nums.length <= 105
1 <= nums[i] <= 105
class Solution {
public:
int minimumOperations(vector<int>& nums) {
int n = nums.size();
unordered_map<int, int> odd, even;
for(int i = 0; i < n; i ++)
{
if(i % 2 == 1) odd[nums[i]] ++;
else even[nums[i]] ++;
}
// Statistics in odd subscripts :
// x0 - x1: The most frequent occurrence x1 Number of numbers x0
// x_ - x2: More times x2 Number of numbers x_
// y Empathy
int x0 = -1, x_ = -1, x1 = 0, x2 = 0;
int y0 = -1, y_ = -1, y1 = 0, y2 = 0;
for(auto x : odd)
{
int num = x.first, cnt = x.second;
if(cnt > x1)
{
x1 = cnt;
x0 = num;
}
}
for(auto x : odd)
{
int num = x.first, cnt = x.second;
if(cnt <= x1 && num != x0)
{
if(cnt > x2)
{
x2 = cnt;
x_ = num;
}
}
}
for(auto y : even)
{
int num = y.first, cnt = y.second;
if(cnt > y1)
{
y1 = cnt;
y0 = num;
}
}
for(auto y : even)
{
int num = y.first, cnt = y.second;
if(cnt <= y1 && num != y0)
{
if(cnt > y2)
{
y2 = cnt;
y_ = num;
}
}
}
if(x0 != y0) return n - x1 - y1;
else return min(n - x1 - y2, n - x2 - y1);
}
};
Take out the smallest number of magic beans
To give you one just An array of integers beans , Each integer represents the number of magic beans in a bag .
Please... From each bag take out Some beans ( It's fine too Don't take out ), Make the rest Non empty In the bag ( namely At least also One Magic bean bag ) Number of magic beans equal . Once the magic beans are removed from the bag , You can't put it in any other bag .
Please return to where you need to take out the magic beans Minimum number .
Example 1:
Input :beans = [4,1,6,5] Output :4 explain :
- We never had 1 Take it out of a magic bean bag 1 A magic bean . The number of magic beans left in the bag is :[4,0,6,5]
- Then we have 6 Take it out of a magic bean bag 2 A magic bean . The number of magic beans left in the bag is :[4,0,4,5]
- Then we have 5 Take it out of a magic bean bag 1 A magic bean . The number of magic beans left in the bag is :[4,0,4,4] A total of 1 + 2 + 1 = 4 A magic bean , The number of magic beans left in the non empty bag is equal . Nothing is better than taking out 4 A plan with fewer magic beans .
Example 2:
Input :beans = [2,10,3,2] Output :7 explain :
- We never had 2 Take it out of one of the bags of magic beans 2 A magic bean . The number of magic beans left in the bag is :[0,10,3,2]
- Then we have... From another 2 Take it out of a magic bean bag 2 A magic bean . The number of magic beans left in the bag is :[0,10,3,0]
- Then we have 3 Take it out of a magic bean bag 3 A magic bean . The number of magic beans left in the bag is :[0,10,0,0] A total of 2 + 2 + 3 = 7 A magic bean , The number of magic beans left in the non empty bag is equal . Nothing is better than taking out 7 A plan with fewer magic beans .
1 <= beans.length <= 105
1 <= beans[i] <= 105
class Solution {
public:
long long minimumRemoval(vector<int>& beans) {
int n = beans.size();
sort(beans.begin(),beans.end());
long long prefixSum[n];
prefixSum[0] = beans[0];
for(int i = 1; i < n;++i)prefixSum[i] = prefixSum[i-1] + beans[i];
long long res = (prefixSum[n-1] - prefixSum[0]) - (long long)beans[0] * (n-1);
for(int i = 1; i < n;++i){
// Take the current position as the final result , All positions on the left have to be reduced to 0
res = min(prefixSum[i-1] + (prefixSum[n-1] - prefixSum[i]) - (long long)(n-i-1) * beans[i],res);
}
return res;
}
};
The maximum sum of the array
Give you a length of n Array of integers for nums And an integer numSlots , Satisfy 2 * numSlots >= n . All in all numSlots Baskets , The number is 1 To numSlots .
You need to put all n Divide the whole number into these baskets , And each basket at most Yes 2 It's an integer . Of a distribution scheme With and Defined as the number of each number and its basket Bitwise and operation The sum of the results .
For example , The digital [1, 3] Put it in the basket 1 in ,[4, 6] Put it in the basket 2 in , The sum of this scheme is (1 AND 1) + (3 AND 1) + (4 AND 2) + (6 AND 2) = 1 + 1 + 0 + 2 = 4 .
Please return and will nums Put all numbers in numSlots The largest of the baskets and .
Example 1:
Input :nums = [1,2,3,4,5,6], numSlots = 3 Output :9 explain : One possible solution is [1, 4] Put it in the basket 1 in ,[2, 6] Put it in the basket 2 in ,[3, 5] Put it in the basket 3 in . The maximum sum of and is (1 AND 1) + (4 AND 1) + (2 AND 2) + (6 AND 2) + (3 AND 3) + (5 AND 3) = 1 + 0 + 2 + 2 + 3 + 1 = 9.
Example 2:
Input :nums = [1,3,10,4,7,1], numSlots = 9 Output :24 explain : One possible solution is [1, 1] Put it in the basket 1
in ,[3] Put it in the basket 3 in ,[4] Put it in the basket 4 in ,[7] Put it in the basket 7 in ,[10] Put it in the basket 9 in . The maximum sum of and is (1 AND 1) + (1 AND 1) + (3 AND 3) + (4 AND 4) + (7 AND 7) + (10 AND 9) = 1 +1 + 3 + 4 + 7 + 8 = 24 . Be careful , Basket 2 ,5 ,6 and 8 It's empty. , This is allowed .
n == nums.length
1 <= numSlots <= 9
1 <= n <= 2 * numSlots
1 <= nums[i] <= 15
class Solution {
public:
int maximumANDSum(vector<int>& nums, int s) {
int n = nums.size(), M = 1;
for(int i = 0; i < s; ++i) M *= 3;
int f[n + 1][M];
memset(f, 0, sizeof(f));
for(int i = 1; i <= n; ++i) {
for(int j = 0; j < M; ++j) {
int t = j, w = 1;
for(int k = 1; k <= s; ++k) {
if(t % 3) {
f[i][j] = max(f[i][j], f[i-1][j - w] + (k & nums[i-1]));
}
t /= 3;
w *= 3;
}
}
}
return f[n][M-1];
}
};
边栏推荐
- 第三章 MapReduce框架原理
- Gridhome, a static site generator that novices must know
- MariaDB的安装与配置
- 解决Intel12代酷睿CPU单线程只给小核运行的问题
- Li Kou: the 81st biweekly match
- Educational Codeforces Round 130 (Rated for Div. 2)A~C
- AcWing:第56场周赛
- Research Report on market supply and demand and strategy of double drum magnetic separator industry in China
- Investigation report of bench type Brinell hardness tester industry - market status analysis and development prospect prediction
- Raspberry pie 4b64 bit system installation miniconda (it took a few days to finally solve it)
猜你喜欢
CMake速成
解决Intel12代酷睿CPU单线程只给小核运行的问题
300th weekly match - leetcode
力扣——第298场周赛
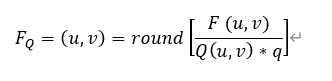
视频压缩编码和音频压缩编码基本原理
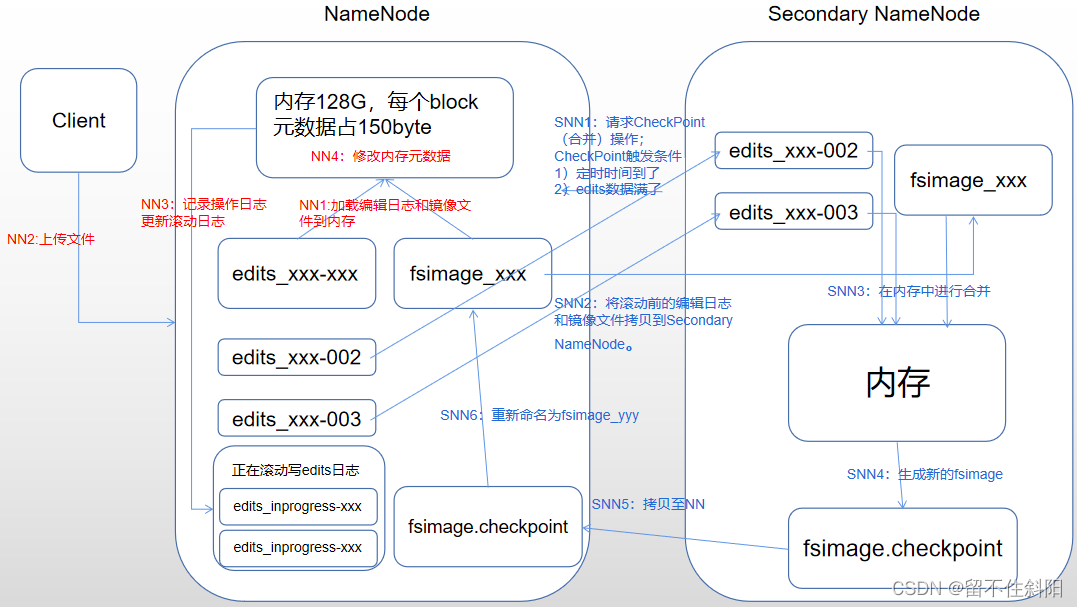
第5章 NameNode和SecondaryNameNode
QT implementation fillet window
![Solve the problem of intel12 generation core CPU [small core full, large core onlookers] (win11)](/img/92/9465a6c9f1ab88c4851a47fabe750c.jpg)
Solve the problem of intel12 generation core CPU [small core full, large core onlookers] (win11)
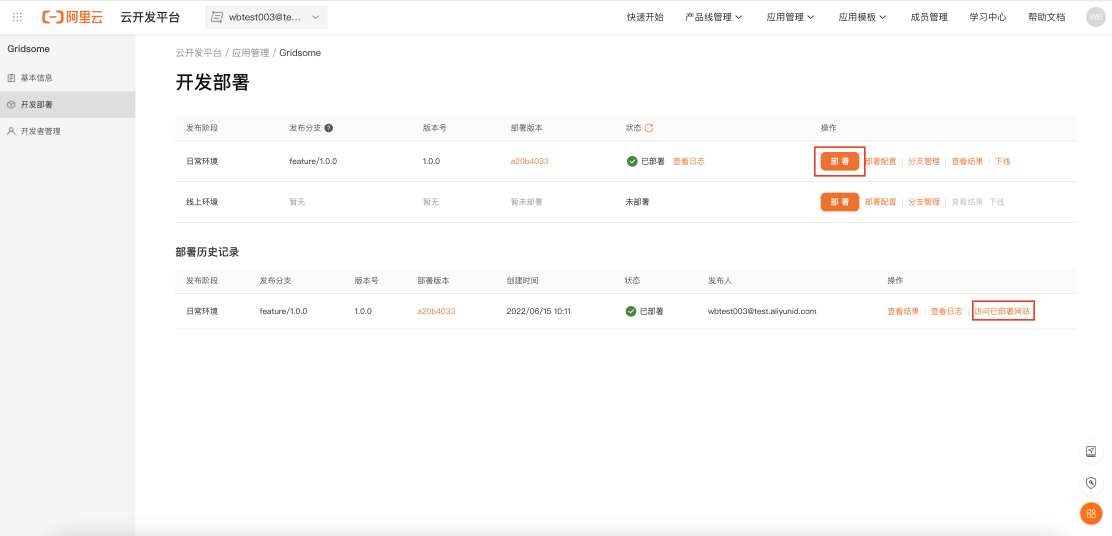
新手必会的静态站点生成器——Gridsome
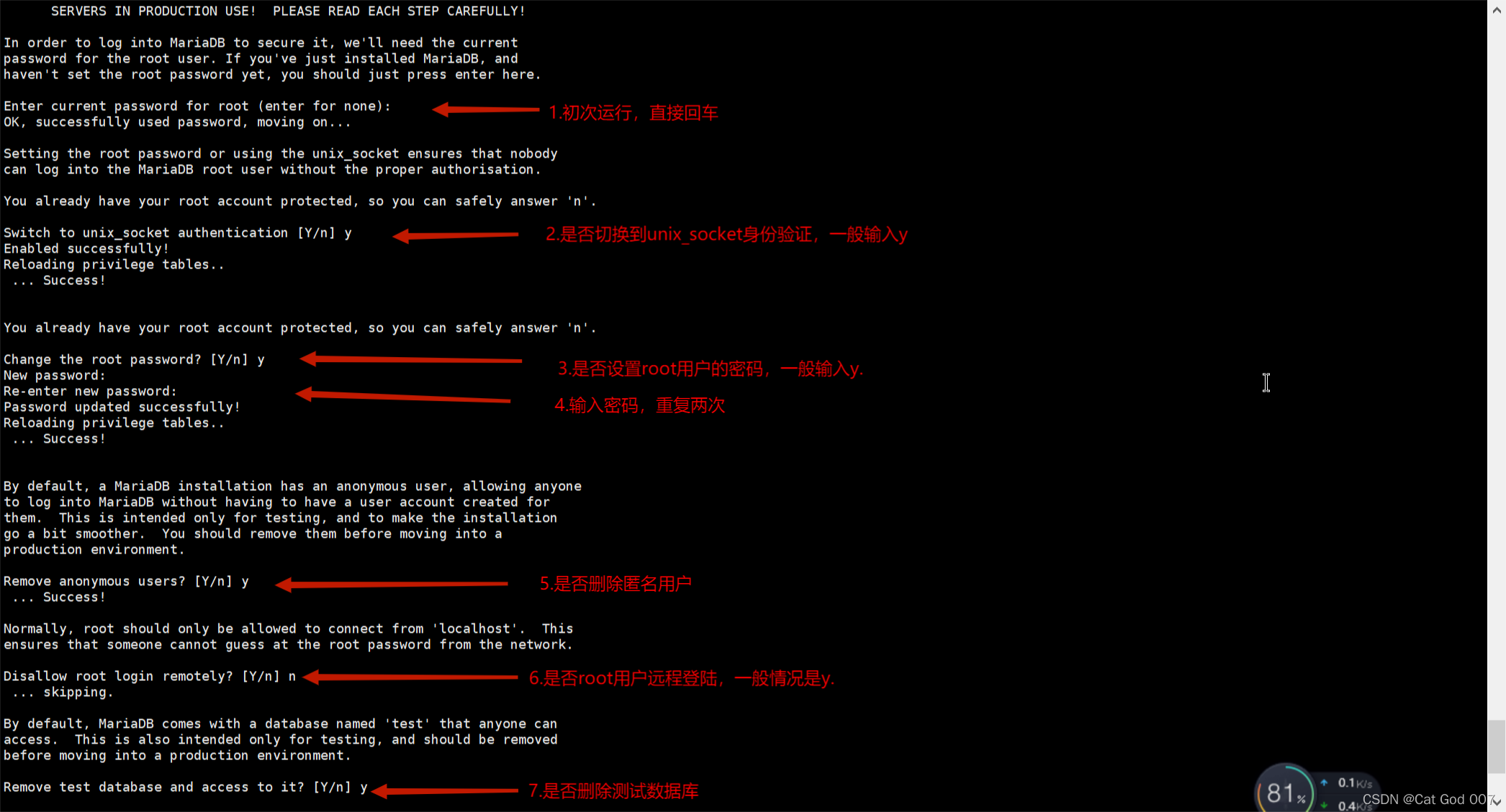
Installation and configuration of MariaDB
随机推荐
Click QT button to switch qlineedit focus (including code)
Codeforces Round #801 (Div. 2)A~C
Codeforces Round #797 (Div. 3)无F
Calculate the time difference
去掉input聚焦时的边框
SQL快速入门
Research Report of desktop clinical chemical analyzer industry - market status analysis and development prospect prediction
图像处理一百题(1-10)
Study notes of Tutu - process
AcWing:第56场周赛
Double specific tyrosine phosphorylation regulated kinase 1A Industry Research Report - market status analysis and development prospect prediction
Codeforces Round #799 (Div. 4)A~H
Solve the single thread scheduling problem of intel12 generation core CPU (II)
Anaconda下安装Jupyter notebook
(lightoj - 1323) billiard balls (thinking)
Research Report on market supply and demand and strategy of China's four seasons tent industry
China double brightening film (dbef) market trend report, technical dynamic innovation and market forecast
力扣leetcode第 280 场周赛
(lightoj - 1370) Bi shoe and phi shoe (Euler function tabulation)
CMake Error: Could not create named generator Visual Studio 16 2019解决方法