Li Kou: the 81st biweekly match

Power button ： The first 81 A fortnight game

6104. Statistical asterisk

Give you a string s , Every time Two Continuous vertical line '|' by a pair . In other words , The first and the second '|' It's a couple , The third and the fourth '|' It's a couple , And so on .

Please return be not in Between vertical line pairs ,s in '*' Number of .

Be careful , Each vertical line '|' Metropolis just Belong to a pair .

Example 1：

 Input ：s = "l|*e*et|c**o|*de|"
 Output ：2
 explain ： Characters not between vertical line pairs are bold and italicized , Get a string ："l|*e*et|c**o|*de|" .
 The first and second vertical lines  '|'  Characters between are not included in the answer .
 meanwhile , The third and fourth vertical lines  '|'  Characters between are not included in the answer .
 There is a total of... Between vertical line pairs  2  asterisk , So we go back to  2 .

Tips ：

• 1 <= s.length <= 1000
• s Only lowercase letters , A vertical bar '|' And asterisk '*' .
• s contain even numbers Vertical lines '|' .

Problem analysis

You can set one at the beginning flag：

• When the number of vertical lines encountered is odd , It means that we are between a vertical line pair , Do not record at this time ‘*’ Value .
• When the number of vertical lines encountered is even , It means that we are not between vertical line pairs , At this time, you can record ‘ *’ Value .

AC Code

class Solution {
public:
    int countAsterisks(string s) {
        int n=s.size(),res=0,cnt=0;
        for(int i=0;i<n;i++)
        {
            if(s[i]=='|')cnt++;
            else if(cnt%2==0&&s[i]=='*')res++;
        }
        return res;
    }
};

6106. Count the logarithm of points that cannot reach each other in an undirected graph

Give you an integer n , Means a sheet of Undirected graph There is n Nodes , The number is 0 To n - 1 . And give you a two-dimensional array of integers edges , among edges[i] = [ai, bi] Representation node ai and bi There is a Undirected edge .

Please return Unable to reach each other Different Number of pairs .

Example 1：

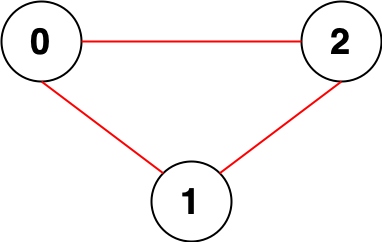
 Input ：n = 3, edges = [[0,1],[0,2],[1,2]]
 Output ：0
 explain ： All points can reach each other , It means that you can't reach each other without point pairs , So we go back to  0 .

Example 2：

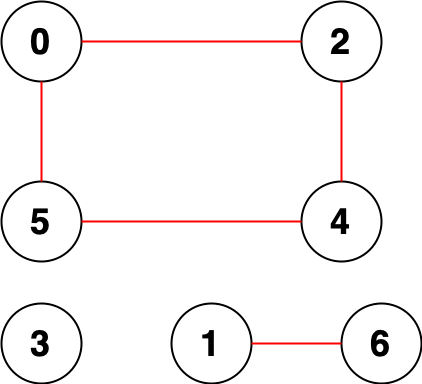
 Input ：n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
 Output ：14
 explain ： All in all  14  Point pairs cannot reach each other ：
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]]
 So we go back to  14 .

Tips ：

• 1 <= n <= 105
• 0 <= edges.length <= 2 * 105
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• No duplicate edges .

Problem analysis

From the example 2 We can see from the above , As long as they are not in a connected block, they cannot reach each other , Then we can connect the points into connected blocks according to the path , Then calculate the number of combinations according to the number of connected blocks and the number of nodes . As for connecting into connected blocks, just use the union search set with record points . Be careful to compress the path, otherwise t.

AC Code

class Solution {
public:
    int mysize[1000000],fa[1000000];
    int find(int x)
    {
        if(x!=fa[x])
            x=find(fa[x]);
        return fa[x];
    }
    long long countPairs(int n, vector<vector<int>>& edges) {
        for(int i=0;i<n;i++)fa[i]=i,mysize[i]=1;
        for(auto i:edges)
        {
            int a=i[0],b=i[1];
            int x=find(a),y=find(b);
            if(x!=y)
            {
                if(mysize[x]>mysize[y])swap(x,y);
                fa[x]=y;
                mysize[y]+=mysize[x];
            }
        }
        unordered_map<int,int>mymap;
        //res Records of the results ,ans Record the points of traversed connected blocks 
        long long res=0,ans=0;
        for(int i=0;i<n;i++)
        {
            int x=find(i);
            // If the current connected block does not traverse , Just calculate the number of combinations 
            if(mymap[x]==0)
            {
            	// The points of the current connected block are considered to have been traversed 
                ans+=mysize[x];
                //（n-ans） Is the number of nodes of other connected blocks that we have not traversed , These nodes are unreachable to the current connected block 
                res += (n - ans) * mysize[x];
                mymap[x]=1;
            }
        }
        return res;
    }
};

6105. Maximum XOR and after operation

I'll give you a subscript from 0 The starting array of integers nums . In one operation , choice arbitrarily Non-negative integer x And a subscript i , to update nums[i] by nums[i] AND (nums[i] XOR x) .

Be careful ,AND It's a bit by bit sum operation ,XOR Is a bitwise XOR operation .

Please execute Any time update operation , And back to nums All elements in Maximum Bitwise XOR and .

Example 1：

 Input ：nums = [3,2,4,6]
 Output ：7
 explain ： choice  x = 4  and  i = 3  To operate ,num[3] = 6 AND (6 XOR 4) = 6 AND 2 = 2 .
 Now? ,nums = [3, 2, 4, 2]  And all elements are exclusive or bit by bit to get  3 XOR 2 XOR 4 XOR 2 = 7 .
 You know  7  Is the largest bitwise XOR sum that can be obtained .
 Be careful , Other operations may also result in bitwise XOR and  7 .

Example 2：

 Input ：nums = [1,2,3,9,2]
 Output ：11
 explain ： perform  0  operations .
 The bitwise XOR sum of all elements is  1 XOR 2 XOR 3 XOR 9 XOR 2 = 11 .
 You know  11  Is the largest bitwise XOR sum that can be obtained .

Tips ：

• 1 <= nums.length <= 10^5
• 0 <= nums[i] <= 10^8

Problem analysis

The nature of XOR operation is ： Under the binary , The same number in the same position is 0, Otherwise 1.

That explains it , If you want to get a value as large as possible through XOR operation , Then every position under binary 1 The number of should be odd . such as 2（10） and 1（01） Exclusive or operation , Binary under the first position and the second position 1 It's just 1 individual ; If it is 2（10） and 3（11）, Then the first position 1 The number of is odd , The second position is even .

The nature of the sum operation is ： Under the binary , The numbers in the same position are 1 Then for 1, Everything else is 0.

The title says you can operate any time , So if in a certain position 1 When the quantity is even （ Not for 0）, We can go through and Operation to turn that position into an odd number （ Just put a binary in this position 1 Number of numbers and One except this position is 0 Everything else is 1 The number can be ）.

in other words , Xor operation , Of each location 1 We can all be odd numbers （ If 0 There's no way ）, Record these 1 The location of , Then convert to decimal number is the result we want .

for example ：3（11）,2（10）,4（100）,6（110）. At this time, the first position 1 The number is 1, The second position is 3, The third position is 2, Then we pass and The operation reduces the third position by one 1, So the binary number obtained by the final XOR operation is ：111. To decimal is 7.

AC Code

class Solution {
public:
    map<int,int>mymap;
    int maximumXOR(vector<int>& nums) {
        int n=nums.size(),res=0;
        //v Save it first 2 Of 0~30 The next power 
        vector<int>v(31,1);
        for(int i=1;i<31;i++)
        {
            v[i]=v[i-1]*2;
        }
        // Find one binary for all numbers 
        for(int i=0;i<n;i++)
        {
            int x=nums[i],cnt=0;
            while(x)
            {
            	// If this position is 1, Then add it to our results , Note that the number of each position can only be taken once , After taking, the number of this position is clear 0
                if(x%2==1)res+=v[cnt],v[cnt]=0;
                cnt++;
                x/=2;
            }
        }

        return res;
    }
};

6107. The number of different die sequences

Give you an integer n . You need to roll one 6 Face dice n Time . Please meet the following requirements , Find out Different The number of dice in a sequence ：

Any in the sequence adjacent Digital greatest common divisor by 1 .
In sequence equal Between the values of , There are at least 2 A number of other values . Formally , If the first i The value of a roll of dice be equal to The first j The second is worth , that abs(i - j) > 2 .
Please return different sequences of The total number . Because the answer can be big , Please correct the answer 10^ 9 + 7 Remainder After the return .

If at least one element of two sequences is different , Then they are treated as different sequences .

 Example  1：

 Input ：n = 4
 Output ：184
 explain ： Some feasible sequences are  (1, 2, 3, 4) ,(6, 1, 2, 3) ,(1, 2, 3, 1)  wait .
 Some infeasible sequences are  (1, 2, 1, 3) ,(1, 2, 3, 6) .
(1, 2, 1, 3)  It's not feasible , Because the first and third dice are equal and  abs(1 - 3) = 2 （ Subscript from  1  Begin to express ）.
(1, 2, 3, 6) i It's not feasible , because  3  and  6  The greatest common divisor of  3 .
 All in all  184  Different feasible sequences , So we go back to  184 .

Tips ：

• 1 <= n <= 104

Problem analysis

Set a n*6 *6 Three dimensional array of f,f[i] [last] [last2] It means ： The length is i Sequence , And the last number is last, The penultimate number is last2 Sequence

Yes f[i] [last] [last2] individual .

Then we extend the length to i+1 Sequence time of , The number added to the tail of enumeration is j, namely f[i+1] [j] [last]

because last and j Is adjacent , therefore j!=last, and gcd(j,last)==1.

meanwhile last2 It can't be equal to j, Because at this time j and last2 The positions of are only separated by a number , Not meeting the conditions .

The state transition equation is ：f[i+1] [j] [last]=(f[i+1] [j] [last] + f[i] [last] [last2])%MOD;

Finally, just enumerate i and j Number of f[n] [i] [j] Add up all the values of , The length is n The number of types of sequences .

AC Code

class Solution {
public:
    int MOD=1e9+7;
    int gcd(int a,int b)
    {
        return a==0?b:gcd(b%a,a);
    }
    int distinctSequences(int n) {
        vector<vector<vector<long long>>>v(n+1,vector<vector<long long>>(7,vector<long long>(7)));
        if(n==1)return 6;
        for(int i=1;i<=6;i++)
            for(int j=1;j<=6;j++)
                if(i!=j&&gcd(i,j)==1)
                    v[2][i][j]++;
        for(int i=2;i<n;i++)
            for(int j=1;j<=6;j++)
                for(int last=1;last<=6;last++)
                    if(j!=last&&gcd(j,last)==1)
                        for(int last2=1;last2<=6;last2++)    
                            if(last2!=j)                          
                                v[i + 1][j][last] = (v[i + 1][j][last] + v[i][last][last2]) % MOD;
        long long res=0;
        for(int i=1;i<=6;i++)
            for(int j=1;j<=6;j++)
                res+=v[n][i][j];                    
        return res%MOD;               
                 
    }
};