当前位置:网站首页>Problem - 1646C. Factorials and Powers of Two - Codeforces
Problem - 1646C. Factorials and Powers of Two - Codeforces
2022-07-06 09:28:00 【你好_Ä】
Problem - 1646C. Factorials and Powers of Two - Codeforces
A number is called powerful if it is a power of two or a factorial. In other words, the number m is powerful if there exists a non-negative integer d such that m=2d or m=d!, where d!=1⋅2⋅…⋅d (in particular, 0!=1). For example 1, 4, and 6 are powerful numbers, because 1=1!, 4=22, and 6=3! but 7, 10, or 18 are not.
You are given a positive integer n. Find the minimum number k such that n can be represented as the sum of k distinct powerful numbers, or say that there is no such k.
Input
Each test contains multiple test cases. The first line contains the number of test cases t (1≤t≤100). Description of the test cases follows.
A test case consists of only one line, containing one integer n (1≤n≤1012).
Output
For each test case print the answer on a separate line.
If n can not be represented as the sum of distinct powerful numbers, print −1.
Otherwise, print a single positive integer — the minimum possible value of k.
Example
input
4
7
11
240
17179869184
output
2
3
4
1
问题解析
这题是说,给你一个数,让你看这个数最少可以由几个2的幂(1,2,4,8等)和阶乘(1,2,6,24)等组成。
首先,每个数都必然会被组合出来,因为所有的数都可以用二进制表示,二进制下有x个1,就说明这个数可以用x个2的次幂来组成,那么我们就是要找在阶乘的组合下,能不能找到更小的x。
题目的数组范围是10^12 ,那么阶乘最大就到15!,算上0!,一共是16个数。我们可以用二进制枚举的方法来枚举(从1枚举到216,看二进制位上哪个位置有1,我们就取哪个数,这样就可以得到这16个数所有的组合)。算出合后,计算:(所用阶乘数+n减去合后用二进制取得的1个数),并维护最小值即可。时间复杂度为O(n*216 )
AC代码
#include<iostream>
using namespace std;
#include<vector>
#include<algorithm>
#include<math.h>
#include<set>
#include<numeric>
#include<string>
#include<string.h>
#include<iterator>
#include<map>
#include<unordered_map>
#include<stack>
#include<list>
#include<queue>
#include<iomanip>
#define endl '\n'
#define int ll
typedef long long ll;
typedef unsigned long long ull;
typedef pair<ll, ll>PII;
const int N = 5050;
int lowbit(ll x)
{
int cnt = 0;
while (x)
{
if (x % 2 == 1)cnt++;
x /= 2;
}
return cnt;
}
signed main()
{
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
vector<ll>ans(16);
ans[0] = 1;
for (int i = 1; i <= 15; i++)ans[i] = ans[i - 1] * i;
int t;
cin >> t;
while (t--)
{
ll n;
cin >> n;
ll res = lowbit(n), sum = 0, cnt = 0;
for (ll i = 1; i <= (1 << 16); i++)
{
sum = 0, cnt = 0;
for (ll j = 0; j <= 15; j++)
{
if (((i >> j) & 1))
{
sum += ans[j];
cnt++;
}
}
if (sum <= n)
{
res = min(cnt + lowbit(n - sum), res);
}
}
cout << res << endl;
}
return 0;
}
边栏推荐
- Differential (one-dimensional, two-dimensional, three-dimensional) Blue Bridge Cup three body attack
- Alice and Bob (2021 Niuke summer multi school training camp 1)
- 渗透测试 ( 5 ) --- 扫描之王 nmap、渗透测试工具实战技巧合集
- 【练习-3】(Uva 442)Matrix Chain Multiplication(矩阵链乘)
- Penetration test (7) -- vulnerability scanning tool Nessus
- 树莓派4B安装opencv3.4.0
- Codeforces Round #802(Div. 2)A~D
- Opencv learning log 27 -- chip positioning
- Auto.js入门
- Opencv learning log 26 -- detect circular holes and mark them
猜你喜欢
Quick to typescript Guide
Analysis of protobuf format of real-time barrage and historical barrage at station B

Basic Q & A of introductory C language
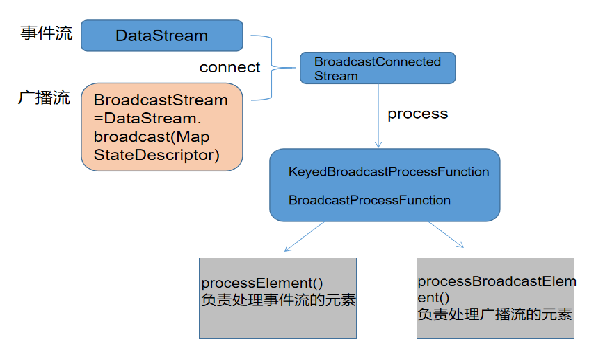
Information security - threat detection - Flink broadcast stream broadcaststate dual stream merging application in filtering security logs
Frida hook so layer, protobuf data analysis
921. Minimum additions to make parentheses valid

Openwrt build Hello ipk
树莓派4B64位系统安装miniconda(折腾了几天终于解决)

B - Code Party (girls' competition)
Essai de pénétration (1) - - outils nécessaires, navigation
随机推荐
QWidget代码设置样式表探讨
1323. Maximum number of 6 and 9
Shell Scripting
快速转 TypeScript 指南
Information security - threat detection - detailed design of NAT log access threat detection platform
最全编程语言在线 API 文档
969. Pancake sorting
【练习-4】(Uva 11988)Broken Keyboard(破损的键盘) ==(链表)
Some problems encountered in installing pytorch in windows11 CONDA
b站 实时弹幕和历史弹幕 Protobuf 格式解析
7-1 understand everything (20 points)
Advancedinstaller安装包自定义操作打开文件
QT实现圆角窗口
F - birthday cake (Shandong race)
[exercise-4] (UVA 11988) broken keyboard = = (linked list)
Information security - threat detection engine - common rule engine base performance comparison
Information security - Epic vulnerability log4j vulnerability mechanism and preventive measures
B - Code Party (girls' competition)
2078. Two houses with different colors and the farthest distance
QT实现窗口置顶、置顶状态切换、多窗口置顶优先关系