当前位置:网站首页>动手学深度学习_卷积神经网络CNN
动手学深度学习_卷积神经网络CNN
2022-08-04 05:29:00 【CV小Rookie】
目录
MLP到CNN的转变
传统的MLP对于图片的处理参数量太大,现在随手拍一张照片像素都在几千万吧,当我们把这张图片送入MLP,假设使用隐藏层不断的降维,里面的参数也得有几十亿,根本没办法训练。另外神经元个数太少也根本无法拟合,学习特征。
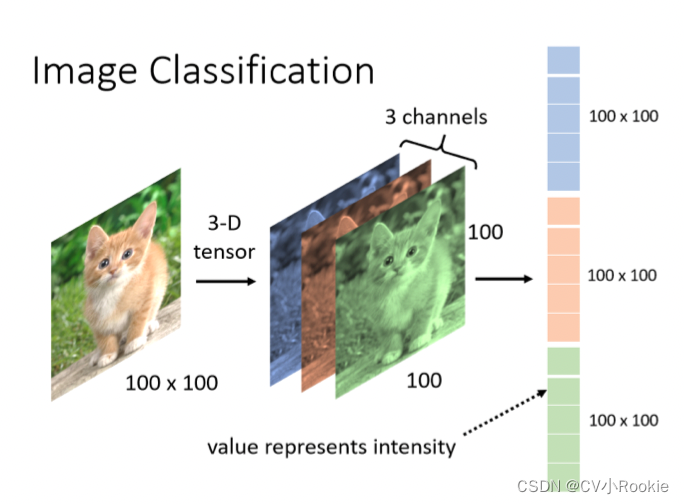

但其实图像中本就拥有丰富的结构,而这些结构可以被人类和机器学习模型使用,卷积神经网络CNN就是利用自然图像中一些已知结构的创造性方法,有效的降低了参数量。
之前在MLP中的时候,输入是一个一维的向量,权重参数W是一个二位的矩阵。现在输入改成了一张图片也就是二维的矩阵,那么对于二维矩阵来说,权重参数就映射到了四维张量:

这里的 其实是为了下面引出卷积做一个代表变换:

可以立即成在像素  位置通过索引
位置通过索引  在正偏移负偏移之间移动覆盖图像。
在正偏移负偏移之间移动覆盖图像。
transitional invariance 平移不变性
不管检测对象出现在图像中的哪个位置,神经网络的前面几层应该对相同的图像区域具有相似的反应
公式  显然不满足平移不变性,因为可以明显看到随着
显然不满足平移不变性,因为可以明显看到随着  的改变
的改变  也发生了变化,这不是我们想看到的。究其原因就因为
也发生了变化,这不是我们想看到的。究其原因就因为  对于
对于  有依赖,所以提出了新的变换:
有依赖,所以提出了新的变换: 原公式就变为:
 这就是二维交叉相关
这就是二维交叉相关
locality 局部性
神经网络的前面几层应该只探索输入图像中的局部区域,而不过度在意图像中相隔较远区域的关系,这就是“局部性”原则。最终,可以聚合这些局部特征,以在整个图像级别进行预测。
继续看上面的公式,当评估  时,我们不应该去考虑离
时,我们不应该去考虑离  太远的参数,所以给
太远的参数,所以给  加上一定的限制:
加上一定的限制: ,新的公式就变为:
,新的公式就变为: 
综上所述,对全联接层使用平移不变性和局部性就可以得到卷积层!
图像卷积
互相关计算:
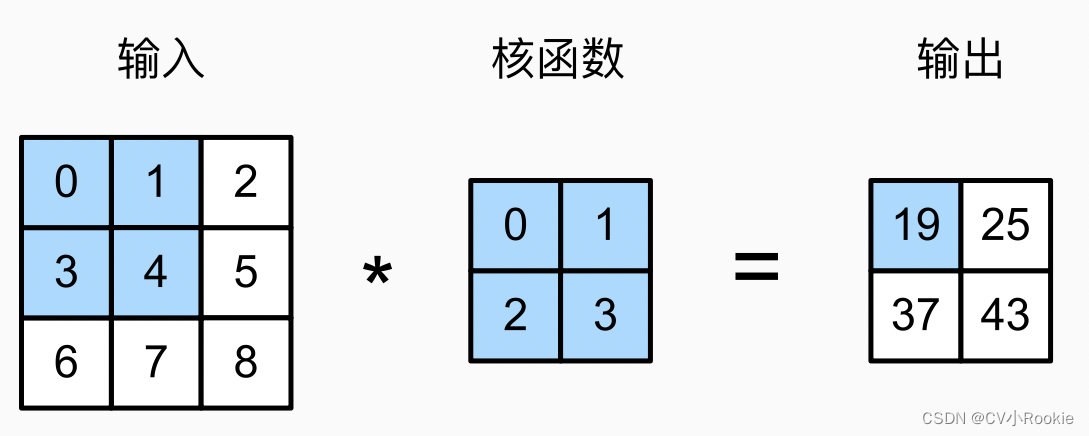
0 X 0 + 1 X 1 + 3 X 2 + 4 X 3 =19
卷积窗口从输入张量的左上角开始,从左到右、从上到下滑动。 当卷积窗口滑动到新一个位置时,包含在该窗口中的部分张量与卷积核张量进行按元素相乘,得到的张量再求和得到一个单一的标量值,由此我们得出了这一位置的输出张量值。
输入大小  ,卷积核大小
,卷积核大小  ,输出大小
,输出大小 
互相关运算的pytorch实现
import torch
def corr2d(X, K): #@save
"""计算二维互相关运算"""
h, w = K.shape
Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
return Y卷积层
前面的数学公式没看懂没问题,看图就懂!

下层的阴影就是卷积核,可以生动的看到卷积核从输入图像左上方依次遍历像素直到结束。
Conv2D 手动实现(利用前面的互相关计算):
class Conv2D(nn.Block):
def __init__(self, kernel_size, **kwargs):
super().__init__(**kwargs)
self.weight = self.params.get('weight', shape=kernel_size)
self.bias = self.params.get('bias', shape=(1,))
def forward(self, x):
return corr2d(x, self.weight.data()) + self.bias.data()padding填充
在应用多层卷积时,我们常常丢失边缘像素。 由于我们通常使用小卷积核,因此对于任何单个卷积,我们可能只会丢失几个像素。 但随着我们应用许多连续卷积层,累积丢失的像素数就多了。 解决这个问题的简单方法即为填充(padding):在输入图像的边界填充元素(通常填充0)。
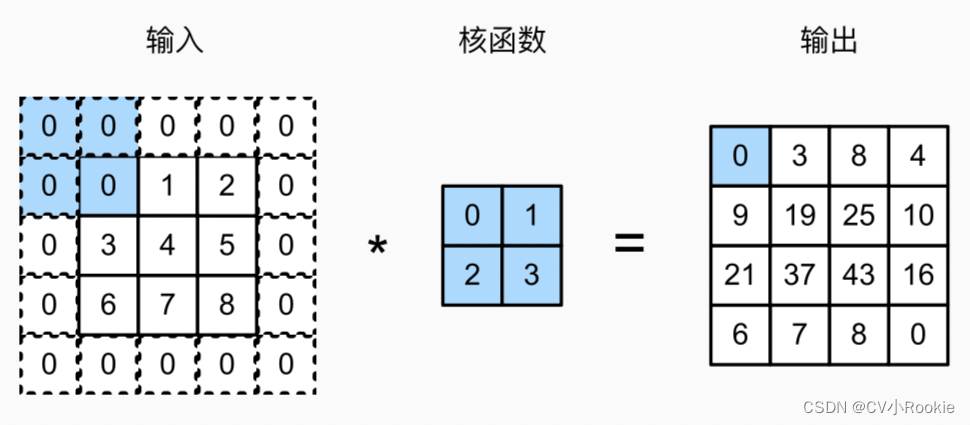
添加  行填充(大约一半在顶部,一半在底部)和
行填充(大约一半在顶部,一半在底部)和  列填充(左侧大约一半,右侧一半),则输出形状将为:
列填充(左侧大约一半,右侧一半),则输出形状将为:
stride步长
在计算互相关时,卷积窗口从输入张量的左上角开始,向下、向右滑动。 在前面的例子中,我们默认每次滑动一个元素。 但是,有时候为了高效计算或是缩减采样次数,卷积窗口可以跳过中间位置,每次滑动多个元素。
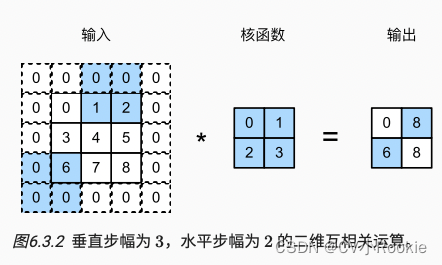
垂直步长  ,水平步长
,水平步长  时,
时,
一般来说我们添加的左右/上下的步长或填充相等的。
1 x 1卷积
卷积本来是识别相邻元素(在宽度或高度上),但 1 x 1 卷积却没有这个能力,因为它只关注当前像素。 其实 1 x 1 卷积的唯一计算发生在通道上,通常用于调整网络层的通道数量和控制模型复杂性。
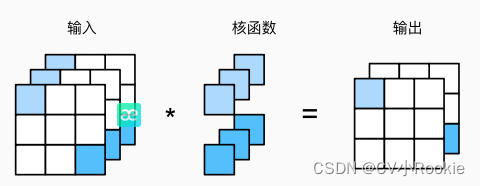
图中展示的就是用 3 输入,2 输出的 1 x 1 卷积核进行通道调整。
pooling汇聚层(池化层)
与卷积层类似,汇聚层运算符由一个固定形状的窗口组成,该窗口根据其步幅大小在输入的所有区域上滑动,为固定形状窗口(有时称为汇聚窗口)遍历的每个位置计算一个输出。 然而,不同于卷积层中的输入与卷积核之间的互相关计算,汇聚层不包含参数。
池化层常见的有最大池化 maximum pooling,平均池化 average pooling 等
其实池化层就像卷积一样,都是滑动窗口遍历图像所有像素,顾名思义,最大池化就是取窗口里的最大值,平均池化就是取窗口里的平均值。池化默认的步长是和核大小一致。
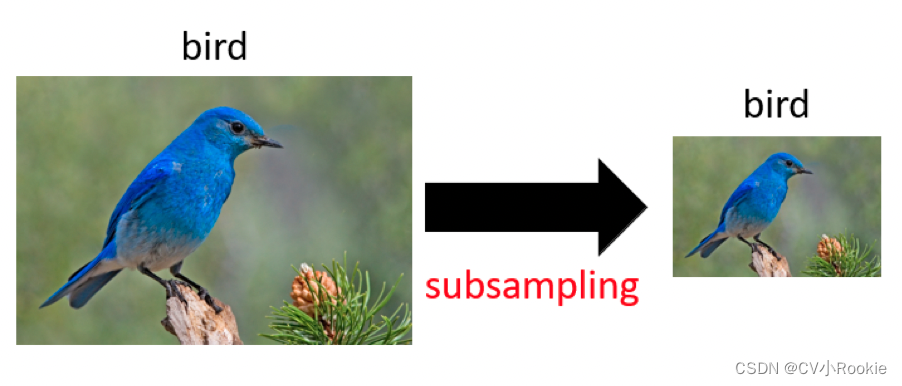
池化层可以有效降低空间维度(比如高度和宽度),减轻卷积神经网络对于位置的过度敏感。
汇聚层的输出通道数与输入通道数相同。
边栏推荐
猜你喜欢
随机推荐
Lombok的一些使用心得
flink-sql大量使用案例
flink-sql所有表格式format
【深度学习21天学习挑战赛】0、搭建学习环境
(十)树的基础部分(一)
ReentrantLock(公平锁、非公平锁)可重入锁原理
字典特征提取,文本特征提取。
读研碎碎念
(十一)树--堆排序
[NSSRound#1 Basic]
智能合约安全——delegatecall (2)
with recursive用法
剑指 Offer 2022/7/12
剑指 Offer 2022/7/9
NFT市场以及如何打造一个NFT市场
yolov3数据读入(二)
Commons Collections1
SQL练习 2022/7/3
0, deep learning 21 days learning challenge 】 【 set up learning environment
Dictionary feature extraction, text feature extraction.